Уравнение прямой

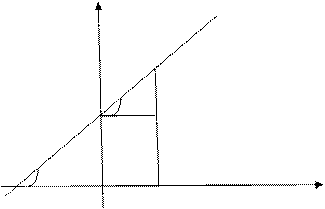
Пусть прямая пересекает ось Оу в точке 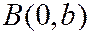и образует с осью Ох угол ().

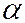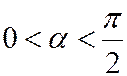Возьмем на прямой произвольную точку 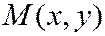. Тогда тангенс угла 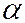наклона прямой найдем из прямоугольного треугольника :

.

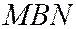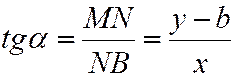у

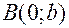
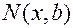
О х

Введем угловой коэффициент прямой 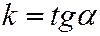, получим

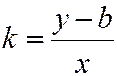
и

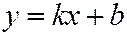. (1)

Уравнение (1) называется уравнением прямой с угловым коэффициентом.

Если 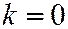, то прямая параллельна оси Ох и ее уравнение имеет вид: .

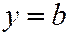Если прямая перпендикулярна оси Ох, то 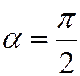и 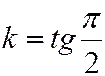не существует, т.е. вертикальная прямая не имеет углового коэффициента. Если она отсекает на оси Ох отрезок равный 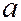, то уравнение такой прямой: .

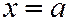Можно показать, что уравнение прямой, проходящей через две точк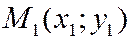и и 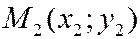, имеет вид:

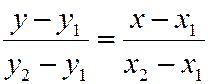. (2)

Выразив y из уравнения (2), получим уравнение вида (1) пр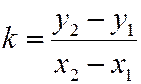и и .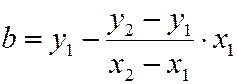

Некоторая точка 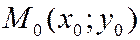и угловой коэффициент 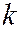также определяют прямую, уравнение которой имеет вид:

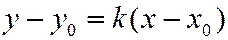. (3)

Определение 2. Пучком прямых, проходящих через данную точку 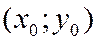, называется множество всех прямых на плоскости, проходящих через данную точку.

Если в уравнении (3) 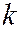- произвольное число, то это уравнение определяет пучок прямых.

Из уравнения (1) всегда можно получить уравнение вида:

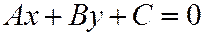, (4)

где коэффициенты А и В не равны нулю одновременно. Уравнение вида (4) называется общим уравнением прямой на плоскости.

Коэффициенты А и В уравнения (4) являются координатами вектора, перпендикулярного к данной прямой: 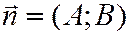- вектор нормали.

Пример 1. Дан треугольник 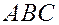с вершинами 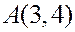, , 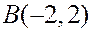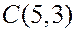. Написать уравнение высоты .

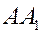Решение. Уравнение высоты имеет вид

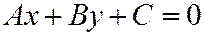
Так как 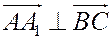, то 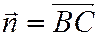– вектор нормали к .

.

.

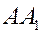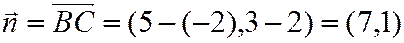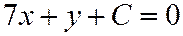Остается найти константу 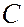, для чего подставим в данное уравнение координаты точки 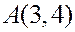. Получаем

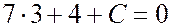
откуда 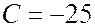, и уравнение прямой имеет вид .

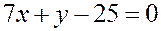Пусть прямая отсекает на осях координат отрезк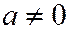и и .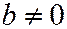

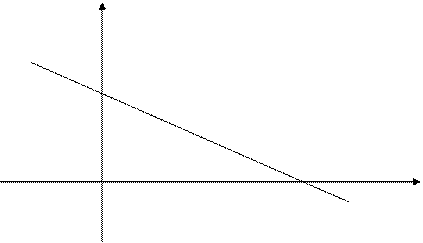
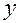
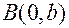
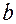
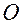
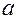
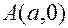
Используя (2), уравнение прямой, проходящей через точк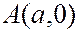и и 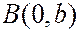, примет вид

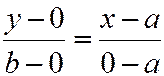
или после преобразований

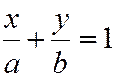. (5)

Уравнение (5) называется уравнением прямой в отрезках.

Дата добавления: 2014-01-07