
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Упражнения. По правилу сложения матриц
|
|
|
|
По правилу сложения матриц
 ,
,
аксиома 4 имеет место.
Итак, аксиомы 1 - 4 справедливы. Аналогично проверяется выполнение аксиом 5 - 8. Таким образом, совокупность  всех квадратных матриц 2-го порядка - линейное пространство.
всех квадратных матриц 2-го порядка - линейное пространство.
1. Доказать, что множество всех геометрических векторов является линейным пространством.
2. Пусть 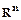 - множество всех упорядоченных наборов
- множество всех упорядоченных наборов 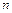 чисел вида
чисел вида  . Пусть
. Пусть 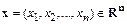 и
и 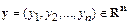 . Положим
. Положим  . Пусть
. Пусть 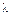 - произвольное действительное число, положим
- произвольное действительное число, положим 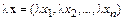 . Доказать, что
. Доказать, что 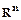 - линейное пространство (
- линейное пространство (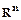 называют линейным пространством
называют линейным пространством 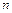 -мерных арифметических векторов).
-мерных арифметических векторов).
3. Доказать, что множество 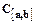 непрерывных на отрезке
непрерывных на отрезке  функций является линейным пространством.
функций является линейным пространством.
Следует отметить, что, вводя линейное пространство, мы отвлекаемся не только от конкретной природы изучаемых объектов, но и от конкретных правил образования суммы векторов и произведения на число, - важно лишь, чтобы эти правила удовлетворяли аксиомам, сформулированным в определении линейного пространства.
Укажем некоторые следствия из аксиом.
1. Единственность нулевого элемента.
Действительно, допустим,  и
и 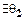 - нулевые элементы, следовательно,
- нулевые элементы, следовательно, 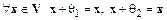 .
.
Имеем 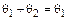 (так как
(так как 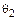 - нулевой), но
- нулевой), но  (так как
(так как  - нулевой), следовательно,
- нулевой), следовательно,  .
.
2. Единственность противоположного элемента.
Пусть 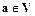 и
и 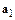 ,
, 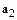 - противоположные элементы для
- противоположные элементы для  , т.е.
, т.е.  ,
,  .
.
Рассмотрим вектор 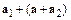 . Имеем
. Имеем
 .
.
С другой стороны,
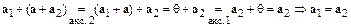 .
.
Теперь всюду далее противоположный элемент для  будем обозначать
будем обозначать 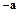 .
.
3. Существование и единственность разности.
Дадим определение разности. Для любых двух векторов  и
и 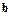 назовем разностью
назовем разностью  и
и 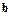 такой вектор
такой вектор 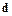 , что
, что  . Обозначим
. Обозначим 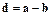 .
.
Положим 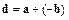 .
.
Имеем
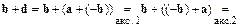
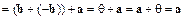 .
.
Следовательно, вектор 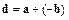 удовлетворяет определению разности.
удовлетворяет определению разности.
Покажем, что он единственный вектор, удовлетворяющий этому определению.
Пусть  .
.
К обеим частям последнего равенства прибавим вектор 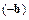 :
:
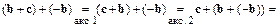
 -
-
таким образом, вектор 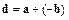 - единственный.
- единственный.
4 Для любого вещественного числа 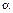
 .
.
5. Для любого вектора 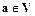
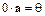 .
.
6. Если 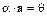 , то либо
, то либо 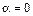 , либо
, либо 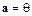 .
.
Для любого вещественного числа 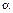 и любого
и любого 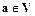 справедливы соотношения:
справедливы соотношения:
7. 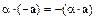 ;
;
8. 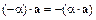 .
.
Следствия 4 - 8 докажите самостоятельно.
10.2. Базис линейного пространства
Определение 2. Пусть  - линейное пространство. Вектор
- линейное пространство. Вектор 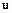 называется линейной комбинацией векторов
называется линейной комбинацией векторов 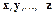 , если найдутся такие числа
, если найдутся такие числа 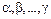 , что
, что
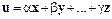 .
.
Определение 3. Система векторов 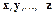 , принадлежащих линейному пространству
, принадлежащих линейному пространству  , называется линейно зависимой, если найдутся такие числа
, называется линейно зависимой, если найдутся такие числа 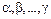 , не все равные нулю одновременно, что выполняется равенство
, не все равные нулю одновременно, что выполняется равенство
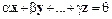 .
.
Определение линейно зависимой системы векторов можно дать в следующей эквивалентной форме, иногда более удобной.
Определение 3'. Система векторов 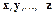 , принадлежащих линейному пространству
, принадлежащих линейному пространству  , называется линейно зависимой, если один из векторов является линейной комбинацией остальных.
, называется линейно зависимой, если один из векторов является линейной комбинацией остальных.
Определение 4. Система векторов 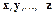 , принадлежащих линейному пространству
, принадлежащих линейному пространству  , называется линейно независимой, если из равенства
, называется линейно независимой, если из равенства
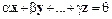
следует, что  .
.
Пример 3. Пусть  - линейное пространство всех матриц порядка
- линейное пространство всех матриц порядка 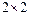 . Доказать, что векторы
. Доказать, что векторы
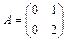 и
и 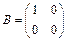
линейно независимы.
Решение. Рассмотрим линейную комбинацию  :
:
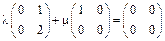 . (10.1)
. (10.1)
Привлекая правила умножения матриц на число и сложения матриц, получим
 . (10.2)
. (10.2)
Равенства (10.1) и (10.2) дают

откуда  , следовательно,
, следовательно, 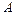 и
и  линейно независимы.
линейно независимы.
Справедливы следующие два утверждения, доказательство которых приведено в лекции 1.
Теорема 1. Всякая система векторов, содержащая нулевой вектор, линейно зависима.
Теорема 2. Всякая система векторов  , содержащая линейно зависимую подсистему
, содержащая линейно зависимую подсистему 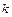 векторов,
векторов, 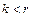 , линейно зависима.
, линейно зависима.
Определение 5. Система векторов  линейного пространства
линейного пространства  называется базисом в
называется базисом в  , если:
, если:
1)  линейно независима;
линейно независима;
2) 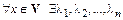 (вещественные числа):
(вещественные числа):
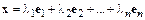 . (10.3)
. (10.3)
Правая часть равенства (10.3) называется разложением вектора  по базису
по базису  , а числа
, а числа 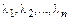 - координатами вектора
- координатами вектора  в базисе
в базисе  .
.
Приведем примеры базисов в конкретных линейных пространствах.
Пример 4.  - линейное пространство всех геометрических векторов, базисом являются любые три некомпланарных вектора.
- линейное пространство всех геометрических векторов, базисом являются любые три некомпланарных вектора.
Пример 5.  - линейное пространство всех многочленов степени
- линейное пространство всех многочленов степени 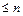 . Показать, что базисом является система векторов
. Показать, что базисом является система векторов 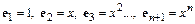 .
.
Решение. Составим линейную комбинацию векторов 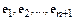 и приравняем ее нулевому вектору:
и приравняем ее нулевому вектору:
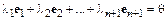 ,
,
или
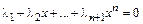 .
.
Имеет место основная теорема алгебры: всякий многочлен степени 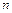 с действительными коэффициентами имеет ровно
с действительными коэффициентами имеет ровно 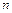 корней, при этом каждый корень считается столько раз, какова его кратность. Это утверждение означает, что равенство
корней, при этом каждый корень считается столько раз, какова его кратность. Это утверждение означает, что равенство 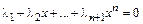 возможно не более, чем в
возможно не более, чем в 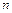 точках, т.е. не может выполняться тождественно (как равенство между векторами в
точках, т.е. не может выполняться тождественно (как равенство между векторами в  ).
).
Следовательно, допущение, что линейная комбинация векторов 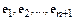 с коэффициентами
с коэффициентами 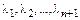 равна нулевому вектору
равна нулевому вектору 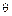 , влечет
, влечет 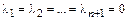 , а это означает, что
, а это означает, что 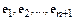 линейно независимы.
линейно независимы.
Пусть 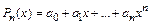 - произвольный многочлен степени
- произвольный многочлен степени 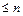 . В последней записи
. В последней записи 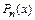 представлен в виде линейной комбинации векторов
представлен в виде линейной комбинации векторов 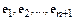 , что вместе с линейной независимостью этих векторов доказывает, что система
, что вместе с линейной независимостью этих векторов доказывает, что система 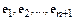 - базис в пространстве многочленов степени
- базис в пространстве многочленов степени 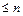 (в соответствии с определением 5).
(в соответствии с определением 5).
Пример 6.  - линейное пространство всех квадратных матриц порядка 2. Показать, что базисом является система
- линейное пространство всех квадратных матриц порядка 2. Показать, что базисом является система
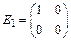 ,
, 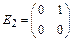 ,
, 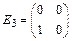 ,
, 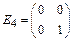 .
.
Решение. Убедимся в том, что система  линейно независима. Составим линейную комбинацию и приравняем ее
линейно независима. Составим линейную комбинацию и приравняем ее 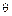 :
:
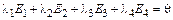 ,
,
или
 ,
,
откуда
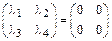 .
.
Последнее равенство дает 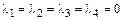 , следовательно, система векторов
, следовательно, система векторов  линейно независима.
линейно независима.
Пусть  - произвольный вектор из
- произвольный вектор из  .
.
Привлекая определения сложения матриц и умножения матрицы на число, получим
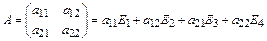 ,
,
т.е. любой вектор из  можно представить в виде линейной комбинации
можно представить в виде линейной комбинации  . В соответствии с определением 5 это вместе с доказанной выше линейной независимостью
. В соответствии с определением 5 это вместе с доказанной выше линейной независимостью  означает, что
означает, что - базис.
- базис.
Упражнение. Доказать, что в линейном пространстве 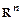 система векторов
система векторов 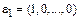 ,
, 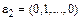 , …,
, …, 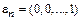 является базисом.
является базисом.
Теорема 3. Пусть  - линейное пространство,
- линейное пространство,  - базис в
- базис в  ,
,  . Координаты
. Координаты  относительно базиса определены однозначно.
относительно базиса определены однозначно.
Доказательство. Пусть  ,
,  и
и  .
.
Имеем
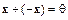 .
.
С другой стороны,
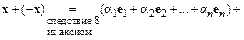
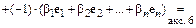
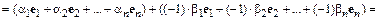

 .
.
Откуда в силу линейной независимости векторов  следует
следует  , т.е.
, т.е.  .
.
Допустив, что вектор  имеет два разложения по базису
имеет два разложения по базису  , мы получили, что эти разложения совпадают, это и означает, что координаты вектора
, мы получили, что эти разложения совпадают, это и означает, что координаты вектора  относительно базиса
относительно базиса  определены однозначно.
определены однозначно.
Теорема доказана.
Замечание. Доказательство Теоремы 3 почти дословно повторяет доказательство аналогичного утверждения для геометрических векторов (Теорема 6 в лекции 1). Как и при доказательстве Теорем 1 и 2, не используется геометрическая природа векторов, а лишь понятия линейной зависимости и линейной независимости. Приведенную ниже Теорему 4 предлагаем доказать самостоятельно (см. Теорему 7 в Лекции 1).
Теорема 4. Пусть  - линейное пространство,
- линейное пространство,  - базис в
- базис в  . При сложении любых двух векторов их соответствующие координаты складываются, при умножении вектора на число каждая координата умножается на это число.
. При сложении любых двух векторов их соответствующие координаты складываются, при умножении вектора на число каждая координата умножается на это число.
Теорема 5. Пусть  - линейное пространство,
- линейное пространство,  - базис в
- базис в  . Всякая система
. Всякая система 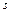 векторов
векторов 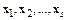 при
при 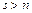 линейно зависима.
линейно зависима.
Доказательство. Достаточно доказать утверждение для 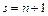 (если
(если 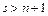 , сошлемся на теорему 2).
, сошлемся на теорему 2).
Пусть 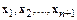 - произвольная система векторов в
- произвольная система векторов в  .
.
Случай 1. Среди 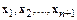 есть
есть 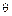 , следовательно, система
, следовательно, система 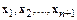 линейно зависима.
линейно зависима.
Случай 2. 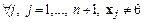 .
.
Так как система  - базис, существуют такие
- базис, существуют такие 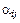
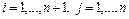 , что
, что
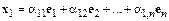 ,
,
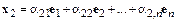 , (10.4)
, (10.4)
……………………………………
 .
.
Среди чисел  есть отличные от нуля (иначе
есть отличные от нуля (иначе 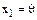 ). Не ограничивая общности рассуждений, можно считать, что
). Не ограничивая общности рассуждений, можно считать, что 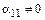 (в противном случае можно перенумеровать базисные векторы), следовательно,
(в противном случае можно перенумеровать базисные векторы), следовательно,
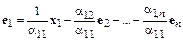 . (10.5)
. (10.5)
Подставив (10.5) во все равенства (10.4), начиная со второго, получим
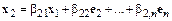 ,
,
…………………………………… (10.6)
 .
.
Векторы 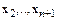 линейно выражаются через
линейно выражаются через 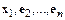 .
.
Если в первом равенстве в системе (10.6) 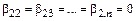 , то
, то 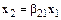 , и система векторов
, и система векторов 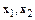 линейно зависима. Тогда, согласно теореме 2, система векторов
линейно зависима. Тогда, согласно теореме 2, система векторов 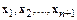 также линейно зависима.
также линейно зависима.
Если же среди 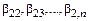 есть отличные от нуля, то, не ограничивая общности рассуждений, считаем, что
есть отличные от нуля, то, не ограничивая общности рассуждений, считаем, что 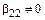 .
.
Из первого равенства в (10.6) имеем
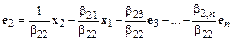 . (10.7)
. (10.7)
Подставим (10.7) во все равенства (10.6), начиная со второго, получим выражения 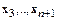 через
через  .
.
Процедуру повторим 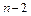 раза и придем к равенству
раза и придем к равенству
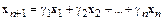 .
.
Один из векторов системы 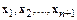 оказался линейной комбинацией остальных, следовательно,
оказался линейной комбинацией остальных, следовательно, 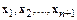 линейно зависимы.
линейно зависимы.
Теорема доказана.
Следствие. Все базисы линейного пространства  состоят из одного и того же числа векторов.
состоят из одного и того же числа векторов.
Действительно, пусть  (I) и
(I) и 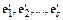 (II) - два базиса в
(II) - два базиса в  .
.
Допустим, 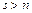 . Так как система (I) - базис, то в силу теоремы 5 это означает, что система (II) линейно зависима. Это противоречит тому, что (II) - базис. Отсюда
. Так как система (I) - базис, то в силу теоремы 5 это означает, что система (II) линейно зависима. Это противоречит тому, что (II) - базис. Отсюда 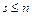 .
.
Допустим теперь, что 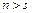 . Так как система (II) - базис, то в силу теоремы 5 это означает, что система (I) линейно зависима. Это противоречит тому, что (I) - базис. Следовательно,
. Так как система (II) - базис, то в силу теоремы 5 это означает, что система (I) линейно зависима. Это противоречит тому, что (I) - базис. Следовательно, 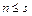 .
.
Вместе эти два заключения дают 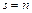 .
.
Определение 6. Число векторов в любом базисе линейного пространства  называется размерностью линейного пространства.
называется размерностью линейного пространства.
Для размерности линейного пространства  принято обозначение
принято обозначение 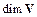 .
.
В рассмотренных примерах:
1) если  - линейное пространство всех геометрических векторов пространства,
- линейное пространство всех геометрических векторов пространства,  ;
;
2) если  - линейное пространство всех многочленов степени
- линейное пространство всех многочленов степени 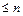 ,
,  ;
;
3) если  - линейное пространство всех квадратных матриц порядка 2,
- линейное пространство всех квадратных матриц порядка 2,  .
.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 380; Нарушение авторских прав?; Мы поможем в написании вашей работы!