Пример. ЕЩЕ будет

Критерий предпочтительной переменной (КПП).

Упорядочивает шаги вперёд из каждой недопустимой точки после первого прихода в неё. Цель упорядочения - рассматривать в первую очередь те маршруты, которые могут быстрее приводят к допустимым решениям. Действие КПП по сокращению перебора реализуется через совместную работу с КПИА: чем раньше будет найдено первое допустимое решение, тем раньше включится в работу КПИА; при нахождении затем лучших допустимых решений действие фильтрующего ограничения по отсеву шагов вперед становится более жестким.

Переменные для шагов вперед упорядочиваются по возрастанию значений (*), где – множество индексов ограничений, невыполненных в точке . В первую очередь движемся по переменной с наименьшей суммой.

Работа КПП в точке (0,0,0,0) определяется табл. 1.3.2.
Таблица 1.3.2.

Номера переменных для возможных шагов вперед
Значения переменных	-8	-1		-4
Порядок шагов вперед по КПП

Идея: в первую очередь рассматривать маршруты, приводящие скорее к возрастанию балансовых переменных y[i] в не выполняющихся ограничениях (при отрицательных a[ij]), т.е. к сокращению множества 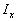. Действие КПП в отличие от КН и КПИА носит эвристический характер и не всегда может привести к желаемым результатам, так как выбор маршрута по наименьшему значению (*) не гарантирует первоочередное движение к допустимым решениям.

Движение по решётке начинается с нулевой точки и заканчивается, когда другие движения невозможны.

Упражнение. Записать алгоритм метода направленного частичного перебора по векторной решетке.

ПРИМЕР.

На рис. 1.3.7. графически показана работа алгоритма при решении задачи (40): упорядочение маршрутов по КПП показано цифрами в кружках; отсеивание точки по КН - соответствующей записью под этой точкой; отсеивание шага вперед по КПИА - соответствующей записью под этим маршрутом; конечные точки отмечены буквой К, а допустимые - буквой Д; решения, перебранные алгоритмом, отмечены точками. Не приводя подробные вычисления по работе алгоритма, опишем агрегированно лишь общий ход его работы и некоторые фрагменты вычислений, поясняющие действие отдельных критериев.

Рис. 1.3.6.
Рис. 1.3.7.

Первой рассматривается точка (0,0,0,0). Она не является допустимой и по КН не отсеивается. КПП упорядочивает возможные шаги вперед следующим образом по номерам переменных: 1, 4, 2, 3. Осуществляется переход в точку (1,0,0,0). Точка (1,0,0,0) является недопустимой, по КН не отсеивается. Возможны шаги вперед по переменным 2, 3 и 4. КПП упорядочивает их следующим образом: 4, 2, 3. Делается шаг вперед в точку (1,0,0,1). Эта точка является допустимой со значением целевой функций Z(1,0,0,1) = 4. Вводится фильтрующее ограничение
Зх[1] + 7x[2]+x'[3] + x[4] + у[0] = 4
Делается шаг назад в точку (1,0,0,0). Следующие по порядку маршруты из точки (1,0,0,0) по 2-й и 3-й переменным отсеиваются по КПИА. Так как все шаги вперед из точки (1,0,0,0) рассмотрены, делается шаг назад. Следующий шаг вперед из точки (0,0,0,0) по 4-й переменной, определяемый КПП, процедурой КПИА не отсеивается. Делается шаг вперед в точку (0,0,0,1). Она является недопустимой и конечной. Осуществляется возврат в точку (0,0,0,0). Следующий по КПП шаг вперед в точку (0,1,0,0) отсеивается по КПИА. Последний возможный шаг вперед из точки (0,0,0,0) по 3-й переменной процедурой КПИА не отсеивается. Осуществляется переход в точку (0,0,1,0), которая оказывается недопустимой и отсеивается по КН. Делается шаг назад в точку (0,0,0,0). Все возможные шаги вперед из точки (0,0,0,0) рассмотрены. Алгоритм закончил свою работу. Найденное к данному моменту допустимое решение (1,0,0,1) является оптимальным решением преобразованной задачи (40). Для исходной задачи (39) с учетом сделанной замены по 3-й переменной оптимальное решение будет определяться точкой (1,0,1,1). Эффективность работы алгоритма может быть определена отношением общего числа возможных решений данной задачи (2⁴) к числу рассмотренных алгоритмом точек (их 5). Выигрыш в числе рассмотренных точек по сравнению с полным перебором равен 3,2.
Работа КПП в точке (0,0,0,0) определяется табл. 1.3.2.
Работа КПИА в точке (1,0,0,0) определяется следующими расчетами. В этой точке значение балансовой переменной фильтрующего ограничения y[0] = 1. Проверка для шагов вперед по 2-й и 3-й переменным приводит к следующим соотношениям C[2]=7>y[0]; C[3]=1=y[0], т.е. оба шага отсеиваются по КПИА.

Работа КН в точке (0,0,1,0) определяется следующими расчетами. В этой точке значения балансовых переменных основных ограничений равны y[1] = -1; y[2]= -8; y[3] = -5, из чего следует, что J_(0,0,1,0)={1,2,3]. Применяя КН к первому ограничению, получаем:
.
Таким образом, точка (0,0,1,0) отсеивается по КН.

Дата добавления: 2014-01-07