Элемент математической культуры как компетенция. III. Выявление основных свойств функций

III. Выявление основных свойств функций.

Лекция № 6-7. Функции в ШКМ (часть II).

Метод-ориентированные ППП

Метод-ориентированные ППП отличаются тем, что в их алгоритмической основе реализован какой-либо экономико-математический метод решения задачи.

К ним относятся ППП:

* математического программирования (линейного, динамического, статистического и т. д.);

* сетевого планирования и управления;

* теории массового обслуживания;

* математической статистики.

Замечание. Графический способ выявления свойств функций см. в пункте I.

1. Нахождение области определения функции.

ЭМК О структурном анализе математических объектов

В математике анализ объектов чаще всего начинают с анализа его структуры.

Поэтому нахождение области определения функции лучше всего начинать с вопроса: «Как устроена функция?».

Задание

По математическому тексту следующей части лекции определите ключевые слова, задающие структуру функции.

а) 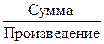функций определены для тех значений аргумента, для которых определены все , т.е. область определения суммы или произведения равна ______________________________ областей определения слагаемых или сомножителей.

Задание

Составьте план нахождения области определения функции в случае а).

1. _______________________________________________________________________

2. _______________________________________________________________________

3. _______________________________________________________________________

Пример. Найти область определения функции f(x) =

1. Арифметический квадратный корень имеет смысл, если подкоренное выражение неотрицательно, т.е. ________________________

Решим неравенство х ² – 4 ³ 0.

Способ 1 (через преобразования)	Способ 2 (методом интервалов)	Способ 3 (графический)
х ^2 ³ ___; ______ ³ 2;     _____________	Нули: х ^2 = 4; х = ______ Интервалы, знаки, ответ:   _____________	Функция: у = х ^2 – 4. Ветви: Пересеч. с ОХ: График: Решение: _____________

2. Арифметический квадратный корень имеет смысл, если подкоренное выражение неотрицательно, т.е. 9 – х ² ³ 0.

Решим неравенство 9 – х ² ³ 0.

_____________________________

3. Найдем пересечение решений:

Ответ: _____________________________

б) Частное двух функций определено для тех значений аргумента, для которых определены числитель и знаменатель и при этом значения знаменателя отличны от нуля.

Пример. Найти область определения функции f(x) = .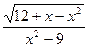

Удобно использовать следующую схему:

1. Выделить выражения, которые не всегда имеют смысл.

2. Определить условия, при которых выделенные выражения имеют смысл и записать их на языке неравенств.

3. Если условие одно, то решить неравенство; если условий несколько, то составить и решить систему неравенств.

Выражение	условие	неравенство
	имеет смысл, если
	имеет смысл, если

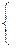
Решим первое неравенство: Решим второе неравенство:

_____________ Ответ: _____________

в) Композиция функция определена для тех значений аргумента, для которых, во-первых, определена внутренняя функция, а, во-вторых, значения внутренней функции принадлежат области определения внешней функции.

Например, функция f(x) = определена тогда и только тогда, когда

4 х – 1 ³ 0 и 2 х – > 0 (при работе с логарифмом удобно проговаривать слова: «логарифм имеет смысл, если выражение, стоящее под знаком логарифма, _________________________»).

2. Нахождение области значений функции.

В вводном курсе математики находить область значений функции будем по графику; в курсе элементарной математики будут рассмотрены аналитические способы нахождения области значений.

3. Нахождение нулей функции.

Чтобы найти нули функции у = f(x), надо составить и решить уравнение __________.

4. Нахождение промежутков возрастания и убывания функции.

Способ 1 (на основе определения).

Используя эскиз графика, определить промежутки возрастания (убывания) функции, а затем доказать возрастание (убывание), пользуясь определением.

Например, для того, чтобы доказать, что функция f(x) возрастает на промежутке I, нужно 1) взять произвольные х ₁и х ₂ из этого промежутка; 2) допустить, что х ₁< х ₂; 3) затем доказать f (х ₁) ___ f (х ₂) (меньшему значению аргумента соответствует ________________ значение функции).

Задание

Оформите идеи способа 1 на языке «дано»- «доказать».

Дано: ______________________________________

Доказать: _________________________________

Дата добавления: 2014-01-07