Хорновские дизъюнкты

Пример.

Пример.

F(x, у) V М(х)

ØM(jon)

Подстановка jon/x делает литералы одинаковыми и к ним можно применить правило резолюции.

{F(jon, у) V M(jon); ØM(jon)}

F(jon, у) - резольвента

Процесс нахождения наиболее общей подстановки, делающей две литеры одинаковыми, называется унификацией.

Рассмотрим унификацию двух литералов

Р(а, х, f(g(y)) и ØP(z, f(z), f(u))

Подстановку S={tl/xl,...} будем строить постепенно слева направо унифицируя несовпадающие литералы.

Пара tl /xl обозначает: tl -подставляемый терм, xl- переменная, вместо которой он будет поставлен. Для того, чтобы унифицировать первые литералы, необходимо сделать подстановку

S={a/z} Р(а, х, f(g(y)); ~Р(а, f(a), f(u))

На втором шаге совмещаем х и f(a), подстановкой

S={a/z, f(a)/x} Р(а, f(a), f(g(y)); ~Р(а, f(a), f(u))

Последняя подстановка

S={a/z, f(a)/x, g(y)/u} P(a, f(a), f(g(y)); ~P(a, f(a), f(g(y)))

Литералы унифицированы. Этот метод дает наиболее общий унификатор. Мы сделали подстановки вместо z и х, и не меняли у. Хотя вместо него можно было поставить любую константу, но это бы сужало доказательство.

Основная проблема в методе резолюций - определить последовательность дизъюнктов, участвующих в резолюции.

Существует класс высказываний, для которых эта задача упрощается. Их подробно исследовал Хорн.

Формула Р1&Р2&...&РÉВ преобразуется в дизъюнкт следующего вида: ~Р1 V ~Р2 V... V ~Рп V В. В нем только один положительный литерал.

Высказывание Р1 & Р2 &... & Pn ÉВ называют продукцией. Многие знания существуют в виде продукций. Например, если птицы летают низко и ветер стих, то скоро пойдет дождь.

Существуют еще два вида формул, который можно преобразовать в хорновские.

l. Pl É B1&B2 разбивается на два дизъюнкта Pl ÉВ1 и Р1É В2

Доказательство.

Р1 É В1 & В2 = ~Р1 V (В1 & В2) = (~Р1 V В1) & (~Р1 V В2) =

(Р1 É В1)&(Р1É В2)

Обобщение Р1 É В1 & В2.. & Вп

2. (Q V S) É В разбивается на два дизъюнкта QÉB и S É B
Доказательство.

(Q V S) É В = ~ (Q V S) V В = (~Q & ~S) V В = (~Q V В) & (~S V В) =

(Q É B)&(S É В)

Обобщение (Q V S... V R) É B

3. Цель доказательства формулируется обычно с помощью квантора существования

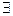x(R(x)&Q(x)...)

Отрицание квантора существования также преобразуется в хорновский

дизъюнкт:

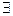~(х (R(x) & Q(x)...)) = 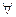x (~R(x) V ~Q(x))

Запрещенный вариант формулы PI É Q V S

Хорновский дизъюнкт содержит не более одного положительного литерала.

Дата добавления: 2014-01-07