Смеси идеальных газов

Закон Дальтона. На практике часто приходится иметь дело с газообразными веществами, близкими по свойствам к идеальным газам и представляющими собой механическую смесь отдельных компонентов различных газов, химически не реагирующих между собой - газовые смеси

Закон Дальтона: полное давление смеси идеальных газов равно сумме парциальных давлений всех входящих в нее ком­понентов:

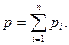(1.7)

где парциальное давление p_i – давление, которое имел бы газ, если бы он один при той же температуре занимал весь объем смеси.

Способы задания смеси. Состав газовой смеси может быть задан массовыми, объемными или мольными долями.

Массовой долей называется отношение массы отдельного компонента m_i к массе смеси m:

g_i = m_i/ m. (1.8)

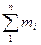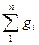Очевидно, что m = и = 1.

Массовые доли часто задаются в процентах. (сухой воздух g_N2 » 77%, g_o2 »23%).

Объемная доля представляет собой отношение приведенного объема газаV_i к полному объему смеси V:

r_i = V_i/ V. (1.9)

Приведенным называется объем, который занимал бы компонент газа, если бы его давление и температура равнялись давлению и температуре смеси.

Для вычисления приведенного объема запишем два уравнения состояния i -ro ком­понента:

p_i V = m_i R_i T; (1.10)

p V_i = m_i R_i T. (1.11)

Первое уравнение относится к состоянию компонента газа в смеси, когда он имеет парциальное давление p_i и занимает полный объем смеси, а второе уравнение - к приведенному состоянию, когда давление и температура компонента равны, как и для смеси, р и Т. Из уравнений следует, что

V_i = Vp_i/ p. (1.12)

Просуммировав соотношения (1.12) для всех компонентов смеси, получим с учетом закона Дальтона:

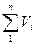= V, откуда 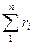= 1.

Объемные доли задают­ся в процентах. Для воздуха r _О2 = 21%, r _N2 = 79 %.

Мольной долей называется отношение количества молей N_i рассматриваемого компонента к общему количеству молей смеси N. Пусть газовая смесь состоит из N ₁ молей первого компонента, N ₂ молей второго компонента и т.д. Число молей смеси

N =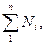

а мольная доля i-гo компонента будет равна N_i/ N.

В соответствии с законом Авогадро объемы моля любого газа при одинаковых р и Т, в частности при температуре и давлении смеси, одинаковы. Поэтому приведенный объем любого компонента может быть вычислен как произведение объема моля mn _i на число молей этого компонента:

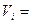μ,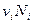

а объем смеси – по формуле 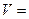μ,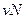

Тогда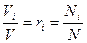

и, следовательно, задание смеси газов мольными долями равнозначно заданию ее объемными долями.

Газовая постоянная смеси газов. Просуммировав уравнения (1.10) для всех компонентов смеси, полу­чим:

.

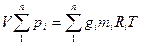pV = mR _см T, (1.13)

где 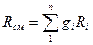. (1.14)

Смесь идеальных газов также подчиняется уравнению Клапейрона.

Т.к R = 8314/ m, то из (1.14) следует, что газовая постоянная смеси, Дж/(кг∙К),

R _см = 8314 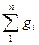/ m_I. (1.15)

Кажущаяся молекулярная масса смеси m_см:

R _см = 8314/ m_см. (1.16)

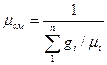(1.17)

m_см = 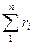m _i. (1.18)

Соотношение между объемными и массовыми долями:

.

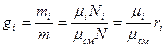Глава 2 Первый закон термодинамики

Дата добавления: 2014-01-07