Примеры и решения

Программирования

	Язык программирования
т и п д а н н ы X		Algol	Pascal	Basic	С
Целое короткое (2 бай­та)	—	Integer Small int	Integer	Short
Целое норм. (4 байта)	Integer	Longint Integer	Long	Long
Действительное норм. (4 байта)	Real	Single	Single	Float
Действ, двойное (8 байт)	—	Real	Double Currency	Long float
Логическое	Boolean	Boolean	Boolean	Boolean
Символьное (1 байт)	—	Char	—	_
Массивы	Array	Array	Dim	П
Записи (структуры)	—	Record	_	Struct

1. Рассмотрим алгоритм обработки двумерного массива. Аналогом двумерного массива в математике является матрица. Общий вид матри­цы А размерности М х N следующий:

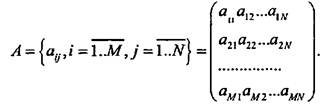
Для матрицы размерностью N * N (квадратной матрицы) определены понятия главной и побочной диагоналей. Элементы главной диагонали —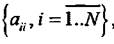, а элементы побочной диагонали —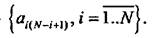

Пусть необходимо построить матрицу, элемент которой а# вычис­ляется как (i + У)², а затем зеркально отобразить ее относительно глав­ной диагонали. Элементам главной диагонали при этом присвоить зна­чение 0. Для решения поставленной задачи воспользуемся структурой дан­ных — двумерный массив целых чисел. На первом этапе построим вло­женный цикл расчета элементов и заполнения массива. На втором этапе проведем «зеркальное отражение» элементов, находящихся под главной диагональю. И, наконец, на третьем этапе обнулим элементы главной диагонали. Блок-схема алгоритма приведена на рис. (N — размерность массива, I и J — индексы).

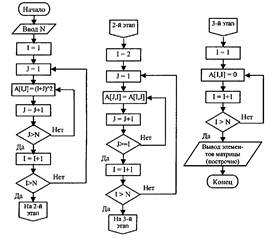
2. Рассмотрим задачу, решение которой основано на преобразовании типов данных.

Пусть необходимо построить алгоритм сложения очень больших целых чисел, для представления которых не подходит тип данных INTEGER, имеющий ограничения на максимально возможные храни­мые значения.

Используем для ввода в алгоритм сложения символьные представ­ления чисел, т.е. рассмотрим каждое число как последовательность символов (например, А = «1234567890» и В = «98765432199»). Для каждого числа посчитаем длину его символьного представления (N — дли­на числа А, М — длина числа В) и присвоим некоторой переменной L значение максимальной длины.

Следующим шагом разместим 3 массива байтов размерностью L + 1 (такова будет максимальная длина в символах полученного результата) и заполним их элементы числовым значением 0. В первый и второй массивы перешлем (начиная с конца) посимвольно числа А и В, преоб­разуя каждый символ в числовое представление (в соответствии с таб­лицей ASCII, это можно сделать, например, вычтя из числового значения кода цифры значение кода символа «0»). При этом в первом и втором массивах получим так называемые двоично-десятичные представления чисел (т.е. когда каждый разряд десятичного числа представляется дво­ичной комбинацией):

A:

B:

C:

Теперь, складывая побайтно (от элемента с номером L+1 до эле­мента с номером 1) числовые значения в массивах А и В и помещая ре­зультат в соответствующий байт массива С, получим двоично-деся­тичный результат сложения двух чисел:

А:

I

В:

1-я

итерация:

С:

о

2-я

итерация:

С:

Результат:

С:

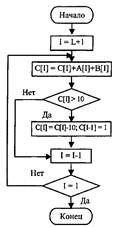
Перенос разряда при сложении может быть осуществлен так, как показано на блок-схеме (рис. 1.В).

Последним шагом решения задачи должно быть преобразование С из двоично-десятичного представления в символьное для вывода ре­зультата.

3. Пусть требуется посчитать количество слов в некоторой после­довательности символов. Определим слово как часть последовательно­сти (ненулевой длины), ограниченную с двух сторон (либо только спра­ва или слева) символом «пробел».

Для решения задачи разместим обрабатываемую последователь­ность в массиве символов размерностью N (где N — длина последова­тельности). При построении алгоритма необходимо учесть, что после­довательность может начинаться или заканчиваться пробелами и может встречаться несколько пробелов подряд.

Блок-схема алгоритма приведена на рис. l.C (L — длина очередно­го слова, NW — количество слов в последовательности, знак пробела обозначен как «__»).

Вопросы и задания

1. Какое максимальное (минимальное) целое значение без знака (со знаком) можно записать в 12 битов?

2. Сколько байтов потребуется для записи Вашей фамилии, имени и отчества?

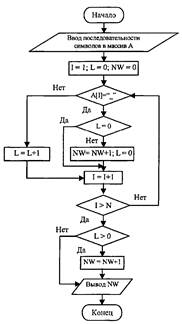
Рис. 1.С

3. Сколько записей «Информация о студенте» можно разместить в 1 мегабайте памяти?

4. Охарактеризуйте различные способы представления числовой информации.

5. Охарактеризуйте разницу между простым и структурированным типом данных.

6. Изобразите в виде блок-схемы алгоритм нахождения максимального (минимального) элемента в двумерном массиве.

7. Постройте алгоритм зеркального отображения элементов двумерного массива размерностью N х N относительно побочной диагонали.

8. Постройте алгоритм формирования одномерного массива, каждый элемент которого представляет собой сумму элементов строки некоторого двумерного массива.

9. Постройте алгоритм вычитания больших целых чисел. Постройте алгоритм ввода данных в структуру «Информация о студенте».

10. Опишите в виде массива записей информацию о студентах группы и по­стройте алгоритм подсчета среднего возраста студентов.

Дата добавления: 2014-01-07