Эллипсометрия и ее применение для контроля толщины слоев диэлектрика и полупроводника

Метод эллипсометрии предназначен для исследования поверхности и тонких слоев, определения оптических постоянных и толщин поверхностных пленок с резкой границей раздела между пленкой и подложкой.

Развитие эллипсометрии долгое время сдерживалось из-за сложной функциональной связи между измеряемыми величинами и параметрами, которые следовало определить. Современные устройства вычислительной техники сделали эллипсометрию удобным методом исследования поверхности и многослойных структур.

Метод эллипсометрии основан на анализе состояния поляризации света, отраженного от исследуемого образца.

Пусть падающий свет является линейно-поляризованным с вектором поляризации 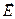(рис.2) и частотой w.

Представим вектор 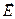в виде векторной суммы двух векторов 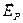и . Вектор 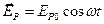принадлежит плоскости падения луча, вектор 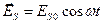пер-пендикулярен этой плоскости. При линейной поляризации разность фаз между 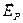и равна нулю. После отражения от образца меняются как фазы, так и амплитуды этих компонент. Сложение двух взаимно перпендикулярных колебаний с разными амплитудами и разностью фаз приводит к образованию эллиптического колебания, при котором конец результирующего вектора 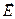описывает эллипс с круговой частотой w.

В самом деле, представим компоненты 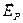и и после отражения в виде

, (1)

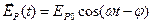. (2)

Исключив временную зависимость в (1) и (2), получим

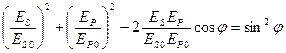, (3)

то есть уравнение эллипса, ориентация которого в координатах р и s зависит от сдвига фаз j компонент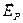и . Если 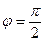, соотношение (3) приобретает вид канонического уравнения эллипса

,

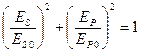а при равенстве амплитуд 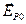=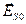соответствует круговой поляризации волны. Пр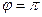и или 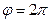(3) описывает колебание с линейной поляризацией.

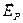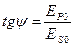Состояние поляризации полностью определяется двумя параметрами - отношением амплитуд и , которое обозначают , и разностью фаз 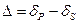компонент 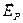и .

Запишем выражения для компонент 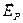и . отраженного луча в комплексном виде

,

.

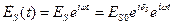Тогда

.

Воспользуемся выражениями для коэффициентов отражения R_p и R_s:

,

,

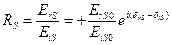где индексы r и i относятся к отраженной и падающей волнам соответственно.

Тогда, обозначив через D разность фаз в падающей i и отраженной r волнах для р и s компонент

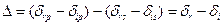
и через tg y - отношение их амплитуд

получим:

(4)

Уравнение (4) есть основное уравнение эллипсометрии.

Величины y и D зависят от характеристик отражающей поверхности (природы, структуры, качества окружающей среды, наличия поверхностных пленок) и измеряются с помощью эллипсометров.

Если на поверхности образца имеется пленка, то его эллипсометрические параметры изменяются, что связано с многократным отражением света на границах разделов пленка - внешняя среда и пленка - подложка и последующей интерференцией отраженных лучей.

Для структуры, изображенной на рис.2, формула (4) приобретет вид:

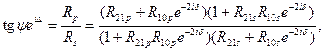(5)

где индексы 0, 1, 2 относятся к подложке, пленке и среде соответственно; δ - оптическая разность хода между отраженными лучами.

Уравнение (5) - это уравнение Друде в однослойной модели.

Для оптической разности хода между отраженными лучами δ легко получить выражение

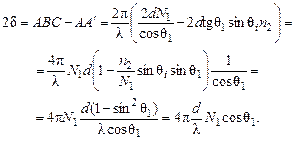(6)

Коэффициенты отражения R в (6) определяются формулами Френеля и являются функциями угла падения луча Q _i и коэффициентов преломления N ₀, N ₁, n ₂.

Таким образом, формулу (5) можно представить в виде

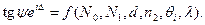(7)

Это соотношение устанавливает связь между измеряемыми эллипсометрическими углами y и D и характеристиками исследуемой системы, подлежащими определению. Величины y и D являются периодическими функциями толщины и повторяются через так называемый эллипсометрический период, равный (250 - 300) нм, поэтому порядок величины d должен быть известен.

Поскольку состояние поляризации света характеризуется только параметрами y и D, из измерений можно определить при одном угле падения также два параметра, задав остальные.

Уравнение (7) наиболее часто используется для определения толщины и показателя преломления прозрачной пленки на подложке с известным показателем преломления (классическая задача эллипсометрии). Решение уравнения Друде можно представить в виде номограмм.

Например, на границе двух непоглощающих сред

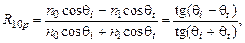
где индексы i и t относятся к падающему и преломленному лучам соответственно. При преобразовании этих формул использовалось соотношение n ₁sinθ _i = n ₀sinθ _t.

Для определения характеристик поверхности материала на границе со средой с показателем преломления n ₁ (не поглощающая среда) уравнение (7) приводится к виду

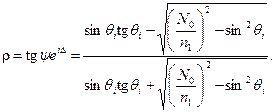(8)

Если известны эллипсометрические параметры поверхности y и D, измеренные при угле падения , то из (9) можно определить показатель преломления

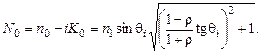(9)

Это единственный случай, когда решение получают в аналитическом виде.

Если измерения проводят на воздухе (n ₁=1) и поглощение в образце отсутствует (K ₀=0), то 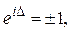и (9) преобразуется к виду

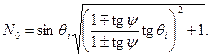(10)

Верхние знаки берутся, если Θ _i< Θ _β, нижние - если Θ _i> Θ _β, где Θ _β - угол Брюстера. При Θ _i= Θ _β в отраженном свете компонента E_{p 0}=0, поэтому y =0 и tg y =0. Отсюда n ₀=tg Θ _β.

Угол Брюстера Θ _β – угол полной поляризации естественного света при отражении от поверхности диэлектрика.

Для структур прозрачная пленка-подложка при известных параметрах подложки и среды находят показатель преломления n ₁ и толщину пленки d. На рис.4а и 4б представлены номограммы Арчера для структур Si - пленка диэлектрика в диапазоне толщин (0 − 100) нм с шагом в 10 нм, а на рис.4 - в диапазоне толщин (0 ÷ 10) нм с шагом в 2 нм. Угол падения луча, длина волны и показатели преломления подложки и среды фиксированы.

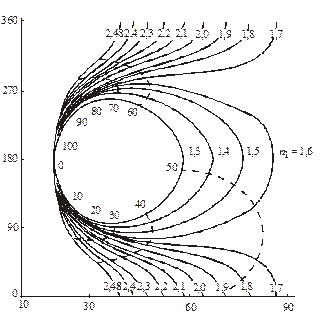Рис.4а. Номограммы Арчера (Y - Δ-номограммы) для структур диэлектрическая пленка - кремний в диапазоне толщин пленки (0 ÷ 100) нм

Рис.4б. Номограммы Арчера (Y - Δ-номограммы) для структур диэлектрическая пленка - кремний в диапазоне толщин пленки (0 ÷ 100) нм

Точность определения величин d и n ₁ во многом зависит от выбора угла падения луча света на образец. На рис.6 представлены зависимости y и D от угла падения для чистого кремния и кремния с пленкой окисла толщиной в 30 нм. Существенное изменение y и D наблюдается для углов θ_i ~(60 − 70)°.

Если слой является поглощающим, число неизвестных (n ₁, k ₁, d) превышает число величин y и D, получаемых при одном измерении. Тогда необходимо провести измерения при двух значениях угла падения либо в двух различных средах.

Для полупроводниковых n-n⁺-структур в области прозрачности эпитаксиального слоя можно определить толщину эпитаксиального слоя и один из параметров подложки, например, концентрацию носителей заряда, связанную с оптическими константами подложки n ₀ и k ₀. Расчеты искомых характеристик проводятся с привлечением численных методов на компьютере.

При выводе формулы (5) предполагалось, что система состоит из однородных слоев с резкой границей между ними. Экспериментальные исследования подтвердили наличие резкой границы в структуре Si-SiO₂, в других же структурах (Ge-GeO₂, Ge-SiO₂, Ge-GeS) существует переходной слой, в котором показатель преломления является переменной величиной. Аналитическое решение таких задач удается получить только для простейших случаев (например, при линейном изменении n).

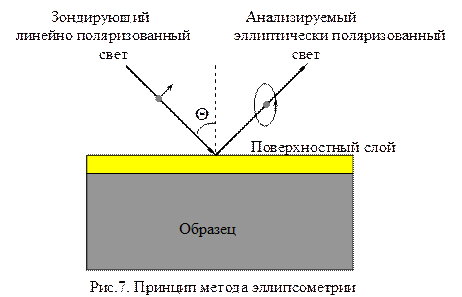
Величины tg y и D определяют с помощью эллипсометров. Принципиальная схема метода эллипсометрии представлена на рис.7.

Дата добавления: 2014-01-07