Начисление простых годовых процентов

Основные схемы начисления процентов

А. В зависимости от базы начисления процентов, известны две основные схемы дискретного начисления процентов: схема простых и схема сложных процентов.

Схема простых процентов (simple interest) предполагает постоянную базу для начисления процентов - одну и ту же первоначальную денежную сумму в течение всего периода начисления.

Инвестированный капитал ежегодно увеличивается на одну и ту же величину.

Схема сложных процентов (compound interest) предполагает переменную базу для начисления процентов. Очередной годовой доход исчисляется не с исходной величины инвестированного капитала (как для простых процентов), а с общей суммы, включающей также и ранее начисленные за предыдущие интервалы и не востребованные инвестором проценты.

В этом случае происходит капитализация процентов, т.е. присоединение начисленных процентов к их базе. Следовательно, база, с которой начисляются проценты, все время возрастает. Сложные проценты иначе называют " проценты на проценты ".

Б. Процентные ставки в зависимости от постоянства значения в течение действия контрактамогут быть фиксированными и плавающими.

В. В зависимости от постоянства интервала времени начисления процентов (год, полугодие, квартал и т.п.) проценты могут быть дискретными и непрерывными ( за бесконечно малые промежутки времени).

Обозначения:

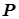- величина первоначальной денежной суммы 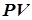- долга, инвестиции,

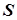- наращенная сумма 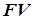в конце срока,

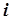% - простая годовая ставка ссудного процента (ставка наращения),

- проценты за весь срок ссуды (ден. ед.),

- продолжительность периода начисления в годах (срок ссуды),

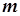- число месяцев ссуды,

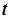- число дней ссуды,

- сумма процентных денег, выплачиваемых за год,

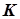- временнáя база для расчета процентов.

Схема простых процентов:

1) начисление процентов в конце интервала начисления (декурсивный способ начисления процентов);

2) простые процентные ставки применяются к одной и той же первоначальной денежной сумме 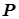в течение всего периода начисления, поэтому база для начисления процентов постоянная;

3) простые ссудные проценты применяются в краткосрочных финансовых операциях (до года).

По схеме простых процентов за каждый год начисляется одинаковая сумма процентных денег .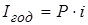

В конце первого года наращенная сумма равна

,

в конце второго года –

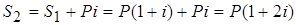, и т.д.,

в конце -ого года сумма составит

.

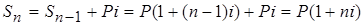Таким образом, приращение капитала (проценты за весь срок ссуды лет) составляют

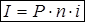(1)

и, как видно, пропорционально сроку ссуды и ставке процента .

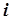Наращенная сумма к концу срока составит

. (2)

Капитализация процентов выражается формулой

. (3)

Процентная ставка 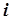(в процентах) есть отношение суммы годовых процентных денег к первоначальной сумме :

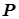. (4)

Заметим, что последовательность наращенных сумм 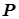, , ,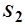..., 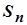образует арифметическую прогрессию с первым членом 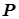и разностью .

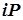· Множитель наращения простых процентов равен отношению наращенной суммы 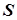к первоначальной сумме :

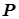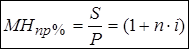(5)

Он показывает, во сколько раз наращенная сумма 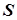больше первоначальной суммы 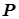. Другими словами, величина характеризует будущую стоимость одной денежной единицы через лет при ставке процента .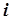

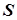
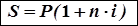
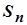
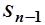
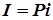
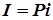
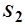
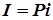
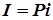
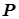
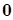1 2....

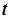
Рис. 1 - График функции наращенной суммы по простым процентам

Пример 4. Ссуда в размере рублей выдана на три года по простой ставке процентов годовых.

1. Найти сумму процентных денег, выплачиваемых за каждый год.

2. Записать последовательность сумм, начисленных к концу первого, второго, третьего года.

3. Найти наращенную сумму за три года.

4. Каковы проценты за весь срок ссуды?

5. Найти множитель наращения за три года.

Решение

По условию задачи, 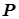=1000, 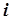=0,2, =3.

1. За каждый год выплачивается сумма процентных денег

руб.

2. В конце первого года наращенная сумма будет равна

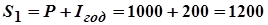руб.,

в конце второго года –

руб.,

в конце третьего года - сумма

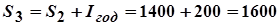руб.

3. Величину наращенной суммы за три года вычислим по формуле (2):

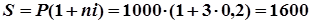руб.

4. Проценты за весь срок ссуды найдем по формуле (1):

руб.

5. Множитель наращения по простым процентам равен

.

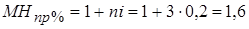Он показывает, во сколько раз увеличилась первоначальная сумма долга 1000 руб. к концу срока ссуды.

Наращение простыми процентами ежегодно по ставке 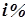годовых дает тот же результат, что и наращение простыми процентами по ставке 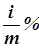за период длительностью (лет).

Дата добавления: 2014-01-07