
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Антагонистические игры (принцип минимакса, седловой элемент, цена игры)
|
|
|
|
В качестве цели при поиске решения антагонистической игры будем рассматривать ситуацию равновесия, то есть устойчивое и выгодное решение.
Ситуация (i*, j*) называется равновесной, если она приемлема для обоих игроков. То есть всякое отклонение от приемлемой ситуации уменьшает выигрыш первого игрока и увеличивает проигрыш второго. Применительно к антагонистическим играм говорят о седловых точках.
Свойства седловых точек:
1. Равноценность. Если в игре несколько седловых точек, то значения функции выигрыша в них одинаковы.
2. Взаимозаменяемость оптимальных стратегий. Игроки могут заменить свои оптимальные стратегии другими оптимальными стратегиями, при этом равновесие не нарушится, а выигрыш (проигрыш) останется неизменным.
Устойчивое решение игры может быть получено путем следующих рассуждений.
Рассмотрим парную конечную игру, то есть два игрока, и они имеют противоположные интересы, причем у каждого из игроков А и В конечное число возможных действий - чистых стратегий.
Пусть игрок 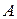 располагает
располагает  стратегиями
стратегиями  , а игрок
, а игрок 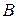 -
- 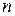 стратегиями
стратегиями 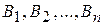 . Целью участников любой матричной игры является выбор наиболее выгодных стратегий, доставляющих игроку
. Целью участников любой матричной игры является выбор наиболее выгодных стратегий, доставляющих игроку 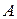 максимальный выигрыш, а игроку
максимальный выигрыш, а игроку 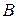 - минимальный проигрыш.
- минимальный проигрыш.
Игрок 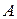 , анализируя платежную матрицу, для каждой стратегии (строки)
, анализируя платежную матрицу, для каждой стратегии (строки)  (
( ) сначала найдет минимальное значение ожидаемого выигрыша
) сначала найдет минимальное значение ожидаемого выигрыша 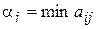 (
( ). А затем из всех
). А затем из всех 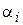 выделит наибольшее число
выделит наибольшее число  и выберет соответствующую ему стратегию
и выберет соответствующую ему стратегию 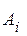 - наиболее предпочтительную в данных условиях. Ее называют максиминной стратегией, поскольку она отвечает величине
- наиболее предпочтительную в данных условиях. Ее называют максиминной стратегией, поскольку она отвечает величине
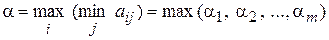 . (1)
. (1)
Число  называется нижней чистой ценой игры (максимином). Оно показывает, какой гарантированный минимальный выигрыш может получить игрок
называется нижней чистой ценой игры (максимином). Оно показывает, какой гарантированный минимальный выигрыш может получить игрок 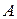 при любых действиях игрока
при любых действиях игрока 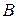 .
.
Игрок 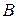 , стремясь минимизировать проигрыш, при выборе наиболее предпочтительной стратегии сначала для каждой стратегии (столбца)
, стремясь минимизировать проигрыш, при выборе наиболее предпочтительной стратегии сначала для каждой стратегии (столбца) 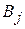 (
(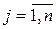 ) найдет максимально возможный проигрыш
) найдет максимально возможный проигрыш  (
(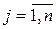 ). А затем среди всех
). А затем среди всех 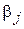 выберет минимальное значение
выберет минимальное значение 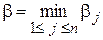 , которому будет соответствовать искомая стратегия
, которому будет соответствовать искомая стратегия 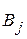 . Ее называют минимаксной, так как она соответствует величине
. Ее называют минимаксной, так как она соответствует величине
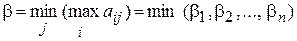 . (2)
. (2)
Число 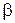 называется верхней чистой ценой игры (минимаксом). Оно показывает, какой гарантированный проигрыш может быть у игрока
называется верхней чистой ценой игры (минимаксом). Оно показывает, какой гарантированный проигрыш может быть у игрока 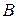 независимо от действий игрока
независимо от действий игрока 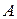 .
.
Таким образом, правильно используя стратегии, игрок 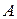 обеспечит себе выигрыш не меньше
обеспечит себе выигрыш не меньше  , а игрок
, а игрок 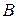 в результате правильного применения своих чистых стратегий не позволит игроку
в результате правильного применения своих чистых стратегий не позволит игроку 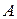 выиграть больше, чем
выиграть больше, чем 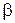 .
.
Принцип, диктующий игрокам выбор наиболее «осторожных» минимаксной и максиминной стратегий, называется принципом минимакса.
Сформулируем утверждение (без доказательства).
В матричной игре нижняя чистая цена игры  не превосходит верхней чистой цены игры
не превосходит верхней чистой цены игры 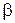 :
: 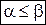 .
.
Общее значение нижней и верхней цены игры  называется чистой ценой игры.
называется чистой ценой игры.
Максиминная  и минимаксные
и минимаксные 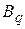 стратегии, соответствующие цене игры
стратегии, соответствующие цене игры 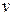 , являются оптимальными стратегиями, а их совокупность – оптимальным решением игры.
, являются оптимальными стратегиями, а их совокупность – оптимальным решением игры.
Элемент  платежной матрицы, стоящий на пересечении строки и столбца, которые соответствуют оптимальным стратегиям
платежной матрицы, стоящий на пересечении строки и столбца, которые соответствуют оптимальным стратегиям  и
и 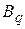 , называется седловым элементом платежной матрицы.
, называется седловым элементом платежной матрицы.
Пример 1. Найти нижнюю и верхнюю цены игры для матрицы
Стратегии игрока 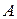
| Стратегии игрока 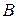
|
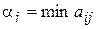
| ||
| B1 | B2 | B3 | ||
| A1 | 0,4 | 0,6 | 0,8 |  = 0,4 = 0,4
|
| A2 | 1,1 | 0,7 | 0,9 |  = 0,7 = 0,7
|
| A3 | 0,7 | 0,3 | 0,5 | 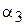 = 0,3 = 0,3
|

| 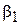 =1,1 =1,1
| 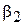 =0,7 =0,7
| 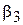 =0,9 =0,9
|
Для этой матрицы видно, что  . Седловая точка
. Седловая точка  , значит, цена игры равна
, значит, цена игры равна .
.
Матричная игра, имеющая седловую точку  , решается в чистых стратегиях.
, решается в чистых стратегиях.
Оптимальными являются чистые стратегии  , образующие седловую точку, цена игры равна
, образующие седловую точку, цена игры равна 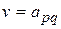 .
.
Решением игры считается тройка 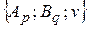 .
.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 967; Нарушение авторских прав?; Мы поможем в написании вашей работы!