
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Математические отношения
|
|
|
|
Для понимания истинного смысла термина отношение рассмотрим несколько математических понятий. Допустим, у нас есть два множества, 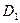 и
и 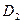 , где
, где 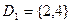 и
и  . Декартовым произведением этих двух множеств (обозначается как
. Декартовым произведением этих двух множеств (обозначается как 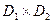 ) называется набор из всех возможных пар, в которых первым идет элемент множества
) называется набор из всех возможных пар, в которых первым идет элемент множества 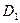 , а вторым — элемент множества
, а вторым — элемент множества 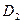 . Альтернативный способ выражения этого произведения заключается в поиске всех комбинаций элементов, в которых первым идет элемент множества
. Альтернативный способ выражения этого произведения заключается в поиске всех комбинаций элементов, в которых первым идет элемент множества 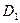 , а вторым — элемент множества
, а вторым — элемент множества 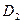 . В данном примере получим следующий результат:
. В данном примере получим следующий результат:
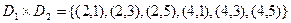 .
.
Любое подмножество этого декартового произведения является отношением. Например, в нем можно выделить отношение 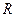 , показанное ниже:
, показанное ниже:
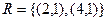 .
.
Для определения тех возможных пар, которые будут входить в отношение, можно задать некоторые условия их выборки. Например, если обратить внимание на то, что отношение 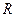 содержит все возможные пары, в которых второй элемент равен 1, то определение отношения
содержит все возможные пары, в которых второй элемент равен 1, то определение отношения 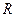 можно сформулировать следующим образом:
можно сформулировать следующим образом:
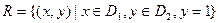
На основе тех же множеств можно сформировать другое отношение, 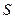 , в котором первый элемент всегда должен быть в два раза больше второго. Тогда определение отношения
, в котором первый элемент всегда должен быть в два раза больше второго. Тогда определение отношения 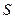 можно сформулировать так:
можно сформулировать так:
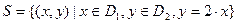
В данном примере только одна возможная пара данного декартового произведения соответствует этому условию:
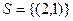 .
.
Понятие отношения можно легко распространить и на три множества. Пусть имеется три множества: — 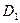 ,
, 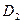 и
и  . Декартово произведение
. Декартово произведение  этих трех множеств является набором, состоящим из всех возможных троек элементов, в которых первым идет элемент множества
этих трех множеств является набором, состоящим из всех возможных троек элементов, в которых первым идет элемент множества 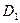 , вторым — элемент множества
, вторым — элемент множества 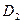 , а третьим — элемент множества
, а третьим — элемент множества  . Любое подмножество этого декартового произведения является отношением. Рассмотрим следующий пример трех множеств и вычислим их декартово произведение:
. Любое подмножество этого декартового произведения является отношением. Рассмотрим следующий пример трех множеств и вычислим их декартово произведение:

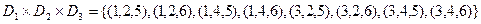 .
.
Любое подмножество из приведенных выше троек элементов является отношением. Увеличивая количество множеств, можно дать обобщенное определение отношения на 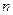 доменах. Пусть имеется
доменах. Пусть имеется 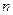 множеств
множеств 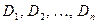 . Декартово произведение для этих
. Декартово произведение для этих 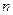 множеств можно определить следующим образом:
множеств можно определить следующим образом:
 .
.
Обычно это выражение записывают в таком символическом виде:

Любое множество 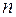 -арных кортежей этого декартового произведения является отношением
-арных кортежей этого декартового произведения является отношением 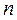 множеств. Обратите внимание на то, что для определения этих отношений необходимо указать множества, или домены, из которых выбираются значения.
множеств. Обратите внимание на то, что для определения этих отношений необходимо указать множества, или домены, из которых выбираются значения.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 532; Нарушение авторских прав?; Мы поможем в написании вашей работы!