Средние величины

Средняя величина (СВ) – единая количественная обобщающая характеристика признака в данной совокупности. Иными словами, СВ – это обобщающий показатель, выражающий типичные размеры количественно варьирующих признаков (возраста, стажа работы, товарооборота, уровня преступности и т.д.) качественно однородных массовых общественных явлений и процессов.

Сущность СВ состоит в том, что в них погашаются случайные отклонения, присущие отдельным единицам совокупности, и выражаются общие закономерности, типичные для всей совокупности. В этом и состоит действие закона больших чисел. Таким образом, одно из главных назначений СВ – сглаживать, элиминировать случайные колебания.

Требования к расчёту СВ:

- массовость данных (т.е. достаточно большое число наблюдений, чтобы можно было делать достоверные выводы);

- однородность совокупности (не следует рассчитывать СВ по качественно разнородным данным, например, среднюю зарплату по директорам и уборщицам).

Необходимость расчёта СВ – наличие такого характерного свойства массовых явлений, как вариация их значений, т.е. колеблемость в один и тот же момент времени. Именно варьирующие признаки (принимающие различные значения) представляют главный интерес для статистики.

Рассмотрим применение в статистическом анализе трёх средних величин:

- средняя арифметическая (среднее значение признака X в данной совокупности);

Mo – мода – наиболее распространенное значение признака X;

Me – медиана – середина ранжированного ряда, т.е. это значение признака X, которое делит ранжированный ряд на 2 равные части.

Напомним: ранжированный ряд – это вариационный ряд, варианты значений признака (X) в котором расположены по возрастанию или убыванию.

Первая ситуация – несгруппированные (индивидуальные) данные

1 задача

Данные о возрасте работников отдела (лет):

34 30 22 48 22

Средний возраст

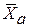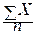= = = 31,2 лет. (n – число слагаемых, то есть единиц совокупности).

Формула расчёта носит название – средняя арифметическая простая.

Модальный возраст Mo = 22 года, т.к. это значение встречается чаще всего.

Для расчёта медианы надо ранжировать исходный ряд (например, по возрастанию):

22 22 30 34 48

Медианный возраст Me = 30 лет, т.к. это значение находится в середине, являясь третьим по ранжиру из пяти.

Вывод:

Половина лиц моложе 30 лет, а другая половина – старше 30.

2 задача

Данные о возрасте работников отдела (лет):

34 30 22 48 22 48

Средний возраст

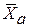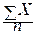= = = 34,0 года.

Модальный возраст Mo = 22 и 48 лет, т.к. эти значения встречаются чаще всего.

Для расчёта медианы надо ранжировать исходный ряд (например, по возрастанию):

22 22 30 34 48 48

Медианный возраст Me = 32 года, т.к. это значение находится в середине, являясь третьим по ранжиру из пяти.

Вывод:

Половина лиц моложе 32 лет, а другая половина – старше 32.

Общее правило для медианы:

Так как носителем медианного значения является та единица, которая находится в середине, то для её определения надо объём ряда (число изучаемых единиц) поделить на 2.

Вторая ситуация – сгруппированные данные (дискретный ряд распределения)

3 задача

Данные о сумме начисленных штрафов за административные правонарушения в районе:

Штраф, руб. (X)						ИТОГО
Число правонарушителей, чел. (m)[1]
Накопленные частоты (S)						---
Расчет S		5+15	20+11	31+2	33+2	---

Средний размер штрафа:

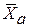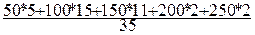= = = 122,9 руб.

Это – средняя арифметическая взвешенная. Расчёт по простой формуле даёт искажённый результат:

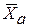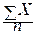= = = 150,0 руб.,

так как учитывает не каждый частный случай, а только варианты значений.

Модальный штраф Мо = 100 руб.

Вывод: наиболее часто правонарушители штрафовались на сумму 100 руб. (больше всего – 15 раз!).

Медианой будет штраф 18-го (35/2=17,5) правонарушителя по ранжиру (в нашей задаче ряд ранжирован). Для чёткого определения медианного значения надо дополнить данные рядом накопленных (кумулятивных) частот (S). Для этого к каждой предыдущей частоте m добавляется последующая.

В первой группе правонарушителей (50 руб.) всего 5 чел, а в следующей (100) их 15, т.е. вместе уже 20 чел. Следовательно, искомый нарушитель оказался в числе этих 15 человек, т.е. его штраф также 100 руб.

Me = 100 руб.

Вывод: у половины правонарушителей штраф 100 руб. и менее, а у другой половины – 100 и более.

Третья ситуация – сгруппированные данные (интервальный ряд распределения)

4 задача

Данные по региону об уровне потребления картофеля в отчётном году:

NN	Уровень потребления, кг/чел/год (x)	Число районов (m)	Центры (середины) интервалов
	Менее 40
	40-60
	60-80
	80-100
	100-120
	Свыше 120
ИТОГО		---

При расчёте среднего значения возникает проблема: что использовать в качестве вариантов значений признака X? Существует правило, согласно которому таковыми считаются центры (середины) интервалов, которые рассчитываются как полусумма их границ. Однако в ряду имеются первый и последний интервалы с одной границей. В этом случае вводится условие, что величина таких открытых интервалов равна величине соседнего. Величина интервала – разница между его границами.

Отсюда:

Первый интервал считаем равным второму, соседнему, имеющему величину 20 (60 - 40). Значит, первый интервал обретает вторую границу, и получаем следующие значения: 20-40. Центр будет равен (20+40)/2=30.

Второй интервал: (40+60)/2=50.

Третий интервал: (60+80)/2=70.

Четвёртый интервал: (80+100)/2=90.

Пятый интервал: (100+120)/2=110.

Шестой интервал приравниваем по величине к пятому, то есть соседнему (величина 20 = 120-100), и имеем: 120-140, отсюда центр: (120+140)/2=130.

Средний уровень потребления по области:

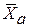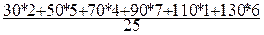= = = 84,4 кг/чел/год.

NN	Уровень потребления, кг/чел (X)	Число районов (m)	Накопленные частоты (S)
	Менее 40
	40-60
	60-80
	80-100
	100-120
	Свыше 120
ИТОГО		---

Расчёт моды и медианы в интервальном ряду распределения имеет особенности, связанные с применением специальных формул. Эти формулы справедливы для рядов с равными интервалами.

Mo = X₀ + h*, где:

- нижняя граница модального интервала;

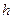- величина модального интервала;

- частоты (соответственно) предмодального, модального и потсмодального интервалов.

Модальный интервал – это интервал с наибольшей частотой. В данном случае это будет интервал 80-100 с частотой m=7.

Mo = 80 + 20*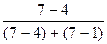= 86,7 кг/чел.

Вывод: наиболее часто встречаются районы с уровнем потребления картофеля 86,7 кг/чел.

Me = X₀ + h*, где:

- нижняя граница медианного интервала;

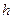- величина медианного интервала;

- накопленная частота предмедианного интервала;

- частота медианного интервала.

Медианный интервал – это интервал, в котором находится середина ранжированного ряда (в данной задаче ряд ранжирован). В данном случае это будет 13-й район (25/2=12,5) по ранжиру. По ряду накопленных частот S найдём интервал, в котором накопленная частота впервые превышает число 13. Это интервал N 4, то есть 80-100.

Me = 80 + 20*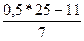= 84,3 кг/чел.

Вывод: половине районов уровень потребления картофеля менее 84,3 кг/чел, в другой половине – более 84,3.

Дата добавления: 2014-01-07