Движение по второму угловому портфелю

Пусть второй угловой портфель не является последним, тогда реализуется событие в), так как второй угловой портфель содержит две ценные бумаги, то есть кроме 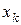в базис войдет . Для простоты: , .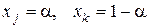

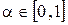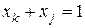Средняя доходность второго углового портфеля , где .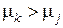

Дисперсия доходности портфеля .

При движении по второму угловому портфелю уменьшается, то есть

.

Для первого портфеля , поэтому в начальной точке

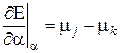
Отсюда .

Критерий выбора: в базис включаем переменную , для которой уменьшение приводит к наиболее быстрому уменьшению 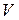, то есть .

2.6.6. Нахождение оптимального портфеля инвестором

Каждому участку критической линии соответствует дуга параболы в пространстве .

Пусть точка, которую выбрал инвестор , тогда определяется автоматически. Пусть располагается между 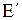и . Тогда в пространстве переменных х оптимальное значени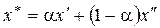е , где находится из условия . Тогда оптимальный портфель инвестора есть: .

2.7. Портфели с безрисковыми ценными бумагами

Определение: Безрисковой ценной бумагой называется ценная бумага с заданной доходностью с нулевой дисперсией.

Пусть имеется 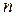рисковых ценных бумаг со средними доходностями и с дисперсиями . Портфель только из рисковых бумаг обозначим .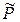

Пусть имеется одна безрисковая ценная бумага с доходностью . Портфель, включающий безрисковую ценную бумагу, обозначим .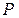

Пусть средняя доходность портфеля 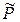есть , дисперсия .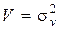

Обозначим через долю средств, вкладываемых в безрисковую ценную бумагу, тогда - доля средств, вкладываемых в рисковые ценные бумаги.

Пусть - доходность портфеля 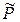, тогда доходность портфеля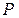 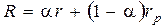. Средняя доходность и дисперсия 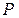будет иметь следующий вид:

;

.

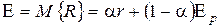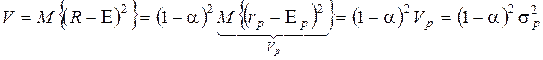Среднеквадратичное отклонение доходности портфеля :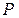

.

Зафиксируем доходность портфеля 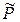, то есть - фиксированная величина. Тогда часть эффективного множества описывается следующими равенствами: , где - параметр.

Когда пробегает значения из , в плоскости получаем отрезок прямой, соединяющий точки и .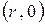

Если точка не лежит на эффективном множестве, то из нее нужно переместиться вправо вниз на дугу кривой .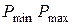

Так как эффективное множество должно быть дугой выпуклой кривой, то точку на дуге 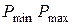нужно выбрать так, чтобы она была точкой касания прямой, проходящей через точку .

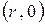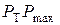Эффективное множество представляет собой линию (см. рис.), где - отрезок прямой, - дуга выпуклой кривой. Портфель 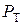называется касательным портфелем.

Полученный портфель называется портфель Тобина.

Вывод: Таким образом, чтобы построить эффективное множество нужно:

1) Отыскать точку 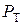и построить первую часть эффективного множества .

2) По алгоритму Марковица отыскать часть эффективного множества . При этом нужно лишь помнить, что в алгоритме Марковица условие остановки будет не 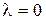, а или .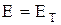

Дата добавления: 2014-01-07