
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Закон Био-Савара-Лапласа
|
|
|
|
Био и Савар (1820г.) исследовали магнитные поля, создаваемые прямолинейным, круговым токами и пытались получить общий закон, который позволял бы вычислить индукцию 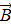 поля, создаваемого проводником с током произвольной формы. Однако этого сделать им не удалось. Лаплас используя принцип су
поля, создаваемого проводником с током произвольной формы. Однако этого сделать им не удалось. Лаплас используя принцип су

|
| Рис.152 |
перпозиции магнитных полей и результаты опытов Био и Савара создал математический закон определения индукции магнитных полей.
Дан проводник с произвольной формы с током, создающий магнитное поле. Найти индукцию 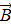 поля в любой точке пространства (на рис.152 точка А).
поля в любой точке пространства (на рис.152 точка А).
Для этого проводник с током разбиваем на элементы тока.
Элементом тока называется векторная величина, равная произведению силы тока I на элемент длины (dl) проводника (рис. 152б), т.е Id . Вычисляем индукцию
. Вычисляем индукцию 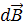 магнитного поля, создаваемого каждым элементом тока Id
магнитного поля, создаваемого каждым элементом тока Id . По закону Био-Савара-Лапласа индукция магнитного поля
. По закону Био-Савара-Лапласа индукция магнитного поля 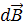 , создаваемого элементом тока Id
, создаваемого элементом тока Id , пропорциональна величине элемента тока, синусу угла α и обратно пропорциональна квадрату расстояния от элемента тока до точки А, т.е.
, пропорциональна величине элемента тока, синусу угла α и обратно пропорциональна квадрату расстояния от элемента тока до точки А, т.е.
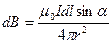 , ,
| (352) |
где 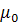 =4p×10-7 Гн/м – магнитная постоянная,
=4p×10-7 Гн/м – магнитная постоянная, 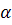 - угол между векторами Id
- угол между векторами Id и
и  .
.
Тогда по принципу суперпозиции результирующая индукция в точке А равна

| (353) |
3.1.3.2. Расчет индукции 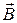 магнитных полей, создаваемых различными токами
магнитных полей, создаваемых различными токами
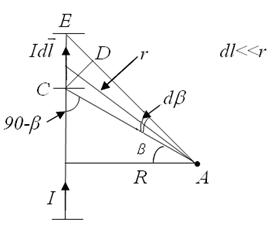
а) Поле, создаваемое прямым проводником с током конечной длины l (рис.153)
Найти В в любой точке А на расстоянии R от проводника.
|
| Рис.153 |
Для этого проводник с током I разбиваем на большое число элементов тока Idl и вычисляем индукцию dB магнитных полей, создаваемых каждым элементом тока.
Индукция 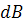 поля, создаваемого элементом тока равна
поля, создаваемого элементом тока равна
 , ,
| (354) |
где α- угол между СЕ и СА. Угол ÐС равен
| ÐС=90-β»ÐЕ, | (355) |
Тогда угол α равен
| α=180-ÐС=180-90+β=90+β. Тогда sinα=sin(90+β)=cosβ | (356) |
Из треугольника СЕД следует, что
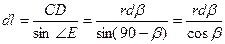 , ,
| (357) |
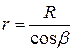 , ,
| (358) |
С учетом (356), (357) и (358) формула (354) запишется:
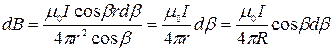 . .
| (359) |
Интегрируя (9) получим:
 . .
| (360) |
где β1и β2 – углы показаны на рис.154.
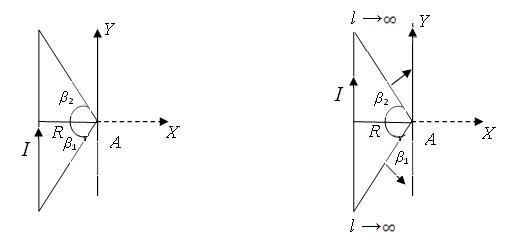
| |
| Рис.154 | Рис.155 |
б) Поле бесконечно длинного проводника с током (рис.155)
Используем формулу (360). При l →¥ углы  ;
; 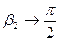 . Тогда индукция В поля, создаваемого бесконечно длинным проводником с током, равна:
. Тогда индукция В поля, создаваемого бесконечно длинным проводником с током, равна:
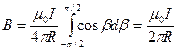 . .
| (361) |
в) Поле кругового тока (рис.156)
Дан круговой ток радиусом R. Найти В поля, создаваемого круговым током, в точках на оси, проходящей через центр кольца, перпендикулярно плоскости кольца (рис.156).
Рис.156
|
Разбиваем круговой ток на элементы тока Idl и по закону Био-Савара-Лапласа найдем индукцию в точке А.
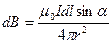 , ,
| (362) |
где α- угол между направлением тока и радиусом  и равен
и равен  .
.
С другой стороны
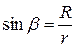 , ,
| (363) |
Тогда
 , ,
| (364) |
Разложим d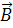 на составляющие
на составляющие
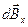 и
и  , т.е.
, т.е.  . (365)
. (365)
Интегрируя (365) получим
 , ,
| (366) |
В выражении (16) интеграл  . Поэтому
. Поэтому
 , (367)
, (367)
|
Подставив (363), (364) в (368), получим
 . .
| (369) |
Из рис.156 следует, что
r =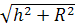 . (370)
. (370)
И с учетом (370) получим
 . .
| (371) | |
в) Магнитное поле в центре кругового тока
В точке О h =0 (рис. 156). Из (371) получим
 . .
| (372) |
г) Поле катушки и соленоида
Катушка или соленоид представляет собой цилиндрический изолированный каркас, на который намотана тонкая проволока плотно виток к витку (рис. 157). На рис. 10 показан разрез сечения диаметра основания катушки или соленоида. Если длина катушки l много больше, чем диаметр d (l>>d), то называется соленоидом, и если  – катушкой.
– катушкой.
На рис.157 крестом сечений проволоки обозначено направление тока от нас, а точкой – на нас. Пусть число витков N, а ток одного витка I.
   
|
| Рис.157 |
Тогда в центре катушки индукция равна:
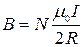 , ,
| (373) |
где R – радиус катушки. Индукция В поля внутри длинного соленоида равна
 , ,
| (374) |
где  - число витков единицы длины соленоида.[12]
- число витков единицы длины соленоида.[12]
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 816; Нарушение авторских прав?; Мы поможем в написании вашей работы!
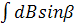 ,
,