
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Движение заряженных частиц в магнитном и электрическом полях
|
|
|
|
а) Движение заряженных частиц в однородном магнитном поле
Пусть положительно заряженная частица q движется со скоростью 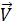 перпендикулярно (
перпендикулярно ( ) силовым линиям магнитного поля. Найти частоту, период обращения частицы и радиус R кривизны траектории (рис.160). Сила Лоренца, действующая на частицу, равна
) силовым линиям магнитного поля. Найти частоту, период обращения частицы и радиус R кривизны траектории (рис.160). Сила Лоренца, действующая на частицу, равна
| Fл= qVB | (378) |
т.к.  ,
, 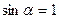 .
.
По закону Ньютона ma=qVB, где 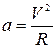 - центростремительное ускорение. Тогда
- центростремительное ускорение. Тогда
 , ,
|
откуда получим формулу радиуса кривизны:
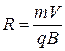 . .
| (379) |
Период обращения частицы равен
 , ,
| (380) |
где 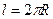 – длина окружности траектории частицы.
– длина окружности траектории частицы.
Циклическая частота равна
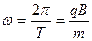 и называется циклоторонной. и называется циклоторонной.
| (381) |
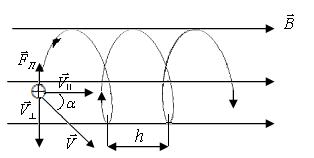
Пусть положительно заряженная частица влетает в однородное магнитное поле под углом α к силовым линиям (рис. 161). Скорость частицы можно разложить на параллельно 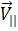 и перпендикулярно
и перпендикулярно 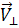 силовым линиям. На частицу будет действовать сила Лоренца
силовым линиям. На частицу будет действовать сила Лоренца
|
| Рис.161 |
и она будет совершать вращательное и поступательное движения (за счет 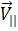 ). Следовательно она будет двигаться по винтовой траектории. Определим шаг винта и радиус R кривизны траектории. Так как период обращения не зависит от скорости, то используя формулу (381) найдем радиус.
). Следовательно она будет двигаться по винтовой траектории. Определим шаг винта и радиус R кривизны траектории. Так как период обращения не зависит от скорости, то используя формулу (381) найдем радиус.
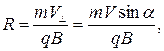
| (382) |
где 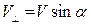 .
.
Шаг винта, т.е. расстояние, пройденное частицей q за один период, с учетом (382) и (380) определяется формулой
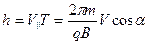
| (383) |
где 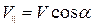 .
.
Движение заряженной частицы в ограниченном пространстве магнитного поля
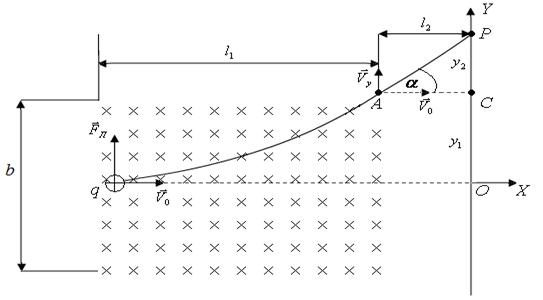
Дано ограниченное пространство магнитного поля размерами 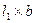 (рис.162), силовые линии которого направлены перпендикулярно плоскости чертежа от нас.
(рис.162), силовые линии которого направлены перпендикулярно плоскости чертежа от нас.
На расстоянии l2 от границы магнитного поля находится экран. Нужно найти отклонение (Y) частицы от прямолинейной траектории, если частица влетает в магнитное поле со скоростью V0 перпендикулярно к силовым линиям.
Из рис. 162 видно, что
| Y=Y 1 +Y 2 | (384) |
Движение частицы в магнитном поле вдоль оси Х является равномерным и поэтому
| l1=V0t | (385) |
Вдоль оси Y на частицу действует сила Лоренца, поэтому она будет двигаться с ускорением
|
| Рис.162 |
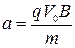
| (386) |
Поэтому 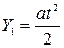 и с учетом (385) и (386) получим
и с учетом (385) и (386) получим
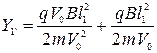 . .
| (387) |
Из треугольника АCР следует, что
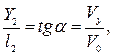  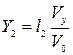 . .
| (388) |
Т.к 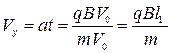 , ,
| (389) |
то (388) получим
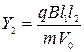 . .
| (390) |
Подставляя (387) и (390) в (384) получим
 . .
| (391) |
б) Движение заряженных частиц в электрическом поле
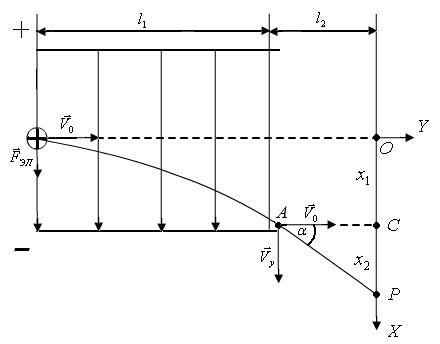
Пусть однородное электрическое поле создано плоским воздушным конденсатором размерами: l1 - длина обкладок конденсатора, d – расстояние межу обкладками (рис.163). На расстоянии l2 от концов пластин конденсатора находится экран. К пластинам приложена разность потенциалов, которая создает однородное электрическое поле, направленное от верхней к нижней пластинам (рис.163). Перпендикулярно к силовым линиям влетает положительно заряженная части q.
Нужно найти отклонение частиц от прямолинейной траектории, т.е
| ОР=Х=Х1+Х2 | (392) |
Движение частицы вдоль оси Y является равномерным прямолинейным, т.к. на нее не действуют силы в этом направлении. Поэтому
| l1=V0t | (393) | |
| ||
| Рис.163 |
Вдоль оси X на частицу действует электрическая сила Fe=qE и движение ускоренное. Поэтому
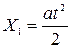 .(394)
.(394)
По второму закону Ньютона ma=qE и
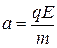 . (395)
. (395)
С учетом (393) и (395) получим
 . .
| (396) |
Из треугольника ACP следует
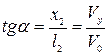 или или 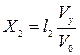 . .
| (397) |
Скорость частицы вдоль оси У равна
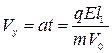 . (398)
. (398)
С учетом (398) формула (397) запишется в виде
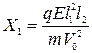 . .
| (399) |
Тогда с учетом (396) и (399) окончательно отклонение равно (392)
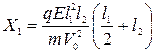 . .
| (400) |
в) Движение заряженных частиц в магнитном и электрическом полях
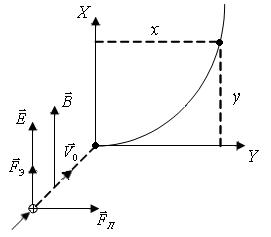
Пусть заряженная частица движется в ограниченном пространстве однородных, сонаправленных электрического и магнитного полей (рис.164). Параметры пространства указаны в предыдущих пунктах. Найти уравнение траектории частицы.
|
| Рис.164 |
Так как на частицу действуют электрическая сила 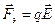 и сила Лоренца
и сила Лоренца 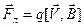 , которые направлены взаимно перпендикулярно (рис.164), то траекторией движения частицы будет парабола, которая показана на рисунке. Координатами параболы являются (391) и (400).
, которые направлены взаимно перпендикулярно (рис.164), то траекторией движения частицы будет парабола, которая показана на рисунке. Координатами параболы являются (391) и (400).
Решая совместно (391) и (400) получим:
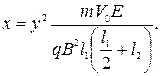
| (401) |
Из (401) можно найти удельный заряд  любой заряженной частицы:
любой заряженной частицы:
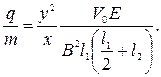
| (402) |
Используя метод, описанный выше, формулу (402) впервые получил Томсон в 1907г и назывался “методом параболы”. Используя этот метод он обнаружил два изотопа неона. В дальнейшем этот метод усовершенствовал Астон и создал прибор масс-спектрограф, используемый для исследования химического состава любого вещества. Методы использования подробно описаны в книгах И.В.Савельева “Электричество и магнетизм”, 2008г стр.247-268.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1757; Нарушение авторских прав?; Мы поможем в написании вашей работы!