Пример расчета коэффициентов уравнения регрессии

Рассмотрим применение регрессионного и корреляционного методов при анализе экономических процессов. Имеются статистические данные о зависимости рентабельности производства продукции (%) по ряду предприятий, производящих одноименную продукцию, от выработки (в стоимостных показателях) на одного среднесписочного работника производственно-промышленного персонала. Полученные данные представлены в таблице (табл. 3):

Таблица 3 – Статистические данные по предприятиям

Номер	Х	Y
		11,20
		11,05
		6,84
		9,21
		9,42
		10,08
		9,45
		6,73
		7.24
		6,12
		7,63
		9,43
		9,46
		7,64
		6,92
		8,95
		9,33
		10,23
		11,77
		7,41
Итого		176,11

Для прогноза результирующего признака Y применим простую модель парной регрессии, в которой используется только одна факторная переменная — Х.

Анализ табличных данных показывает наличие прямой линейной зависимости между факторным Х (выработки продукции) и результативным признаком Y (рентабельностью производства). Тесноту и направление связи между факторным и результативным признаками определим с помощью коэффициентом корреляции r.

где X_i и Y_i - значения факторного и результативного признаков соответственно; n – объем выборки (число пар исходных данных).

Для рассматриваемого примера значение коэффициента корреляции составляет:

r =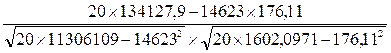= 0,955

Для описания рассматриваемого экономического процесса с помощью метода экономико-математического моделирования рассчитаем параметры уравнения регрессии: Y_теор = b₀ + b₁·X.

Данные для расчета параметров представим в табл.4

Таблица 4 – Таблица расчетных данных для определения

коэффициентов уравнения регрессии

X-n	Y-Q	X*X	Y*Y	X*Y	X*X*X	X*X*X*X	Y*X*X	У теор.линия	Утеор.параб.	(Уфакт-Утл)2	(Уфакт-Утпар)2
	11,2		125,44	10158,4		6,76751E+11	9213668,8	10,3	10,39	0,739	0,66
	11,05		122,1025	10232,3		7,35265E+11	9475109,8	10,5	10,60	0,295	0,21
	6,84		46,7856	3461,04			1751286,24	6,8	6,88	0,000	0,00
	9,21		84,8241	6824,61		3,0149E+11	5057036,01	8,9	8,74	0,101	0,22
	9,42		88,7364	7432,38		3,87532E+11	5864147,82	9,3	9,19	0,012	0,05
	10,08		101,6064	8961,12		6,24607E+11	7966435,68	10,2	10,20	0,011	0,01
	9,45		89,3025	8259,3		5,83507E+11	7218628,2	10,1	10,04	0,363	0,35
	6,73		45,2929	3432,3				6,9	6,91	0,021	0,03
	7,24		52,4176	3829,96			2026048,84	7,0	7,04	0,040	0,04
	6,12		37,4544	2570,4				6,1	6,34	0,001	0,05
	7,63		58,2169	5180,77		2,12559E+11	3517742,83	8,4	8,19	0,519	0,32
	9,43		88,9249	8222,96		5,78184E+11	7170421,12	10,0	10,02	0,366	0,35
	9,46		89,4916	8741,04		7,28933E+11	8076720,96	10,5	10,57	1,059	1,24
	7,64		58,3696	4637,48		1,35755E+11	2814950,36	7,7	7,61	0,007	0,00
	6,92		47,8864	3127,84			1413783,68	6,4	6,53	0,304	0,15
	8,95		80,1025	6524,55		2,8243E+11	4756396,95	8,8	8,63	0,027	0,10
	9,33		87,0489	7408,02		3,9745E+11	5881967,88	9,4	9,23	0,001	0,01
	10,23		104,6529	8634,12		5,07423E+11	7287197,28	9,8	9,73	0,193	0,25
	11,77		138,5329	11887,7		1,0406E+12		11,2	11,55	0,281	0,05
	7,41		54,9081	4601,61		1,48719E+11	2857599,81	7,8	7,72	0,188	0,10
Сумма
	176,11		1602,097	134127,9		7,62558E+12				6,528	6,19

Коэффициенты b₁ и b₀ линейного уравнения регрессии определяются по формулам (13), (13а):

, .

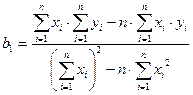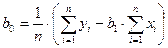Подставив данные из таблицы получим следующие значения коэффициентов: b₀ =2,423; b₁ = 0,00873.

Для примера линейное уравнение регрессии имеет вид:

Y_теор = 2,423 + 0,00873·X.

Коэффициент b₁ характеризует наклон линии регрессии. b₁ = 0,00873 и это означает, что при увеличении Х на единицу ожидаемое значение Y возрастет на 0,00873. Отсюда b₁ может быть интерпретирован как прирост нормы рентабельности, который варьирует в зависимости от средней выручки. Свободный член уравнения b₀ =2,423 у. е.; это значение Y при X, равном нулю. Поскольку маловероятно значение выработки, равное нулю, то можно интерпретировать b₀ как меру влияния на величину рентабельности других факторов, не включенных в уравнение регрессии.

Регрессионная модель может быть использована для прогноза уровня рентабельности, (который будет на предприятии, например, где средняя выработка на одного работника составит 600 руб.)

Для того чтобы определить прогнозируемое значение, следует Х = 600 подставить в регрессионное уравнение:

Y = 2,423 + 0,00873 • 600 = 7,661.

Отсюда прогнозируемый уровень рентабельности для предприятия со средней выработкой 600 рублей на одного рабочего ППП составляет 7,661 %.

Коэффициент эластичности для модели Э = 0,00873 = 0,7249, т. е. при увеличении средней выработки на одного работника по отдельному предприятию 1% уровень рентабельности в среднем вырастет на 0,7%.

Изменение уровня рентабельности производственного предприятия, определяемое средней выработкой на одного работника можно определить также с помощью параболической зависимости. Для определения коэффициентов параболы используются формулы, полученные на основе решения системы уравнений (15).

Данные для расчета коэффициентов приведены в табл. 4

В результате расчетов получено уравнение параболы со следующими коэффициентами:

y = 4,7893+0,00156 x+5,1·10 ^–6 x² .

Для проверки адекватности моделей, построенных на основе линейного и параболического уравнения регрессии, проверим значимость каждого коэффициента, используя формулы (20-23).

Для коэффициента b₀ линейной модели

Для коэффициент b₁ линейной модели

.

Для коэффициента b₀ параболической модели

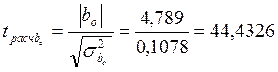
Для коэффициента b₁ параболической модели

Для коэффициента b₂ параболической модели

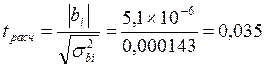
t_кр = 2,1 при α = 0,05; n=n-k-1=20-1-1=18

Из приведенных расчетов видно, что при α = 0,05 значимыми является коэффициенты линейного уравнения регрессии и параболического, за исключением коэффициента, стоящего перед квадратом факторного признака, что свидетельствует об отсутствии квадратичной зависимости между рассматриваемыми признаками моделируемого экономического процесса.

Проверка адекватности всей модели осуществляется с помощью расчета
величины средней ошибки аппроксимации .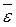

Значение средней ошибки аппроксимации для линейной модели составляет

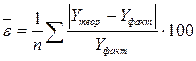= 4,07 %

для параболической модели составляет

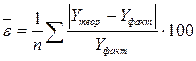= 4,14 %

Полученные расчетные данные ε показывает очень малое расхождение между полученными линейной и параболической моделями. Таким образом можно утверждать, что связь между факторным и результативным признаками носит линейный характер и рассматриваемый экономический процесс можно аппроксимировать с помощью линейного уравнения регрессии.

Дата добавления: 2014-01-07