Локальные бифуркации коразмерности один

В системах второго порядка возможны две локальные бифуркации коразмерности один: в первом случае в нуль обращается одно из действительных собственных чисел равновесия, во втором — вещественная часть пары комплексно сопряженных собственных чисел. Будем называть равновесие кратным, если 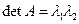, и нейтральным, если 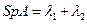. Отметим, что нейтральное равновесие может быть как седлом ( 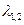действительны), так и сложным фокусом или центром ().

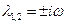2.1. Бифуркация коразмерности один — двукратное равновесие

Пусть при некоторых значениях па­раметров у данного положения равновесия 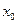одно из собственных чисел обращается в нуль:

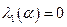; (4.5)

следовательно, 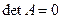. Эта бифуркация аналогична бифуркации коразмерности один «двукратное равновесие» для систем на прямой.

Модельная система для такой бифуркации зависит от одного параметра и имеет вид:

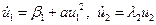. (4.6)

Для данной бифуркации имеются два условия невырожденности. Одно из них: 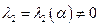, т. e. 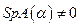. Второе: . Это условие аналогично условию невырожденности для соответствующей бифуркации в одномерных системах и, как и там, обеспечивает двукратность положения равновесия.

Система (4.6) имеет две различные бифуркационные диаграммы, определяемые знаком 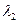. Рассмотрим случай 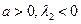(случаи других сочетаний знаков 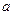и 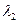приводятся к данному с помощью замены 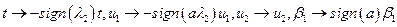. При в системе (4.6) имеются два грубых положения равновесия — устойчивый узел и седло. При они сливаются, образуя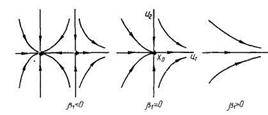

Рис 4 2 Бифуркационная диаграмма и фазовые

портреты для бифуркации «двукратное равновесие»

на плоскости (случай а>0, \з<0)

«седлоузел» — возникает негрубая система. При равновесия исчезают (рис. 4.2). Как и в одномерном случае, говорят, что происходит «срыв равновесия».

Примечание. Поясним чуть подробнее отмеченную выше аналогию между бифуркациями «двукратное равновесие» в одномерном и двухмерном случаях. При наличии одного критического (нулевого) собственного числа перестройка положений равновесия в системе (4.1) происходит на (гладко зависящей от параметров) одномерной инвариантной кривой в фазовой плоскости и описывается одним уравнением для некоторой координаты 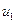на этой кривой. Каноническое описание бифуркаций на данной кривой дается соответствующим одномерным модельным уравнением (3.6). Близкие к инвариантной кривой траектории экспоненциально приближаются к ней или удаляются от нее при 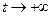в зависимости от знака ненулевого собственного числа 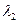, что и описывается уравнением для и₂ в системе (4.6). Аналогичным образом строятся модельные системы для рассматри­ваемых далее бифуркаций «трехкратное равновесие» и «четырехкратное равно­весие» в системах на плоскости.

Сформулированные утверждения следуют из принципа сведения.

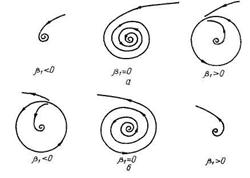
2.2. Бифуркация коразмерности один — нейтральное равновесие (бифуркация рождения цикла)

Пусть при некоторых значениях пааметров у данного положения равновесия 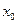пара комплексно-сопряженных

Рис 4 3 Бифуркационные диаграммы и фазовые портреты для бифуркации «нейтральное равновесие (рождение цикла)» а — 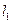<0, b — 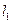>0

собственных чисел выходит на мнимую ось:

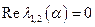, (4.7)

т. е. 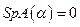, в то время как 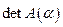>0.

Модельная система для данной бифуркации коразмерности один зависит от одного параметра и может быть записана в комплексном виде:

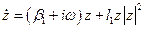, (4.8)

где 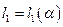— действительное число, .

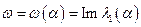Для данной бифуркации имеются также два условия невырожденности: 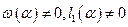. Величина 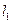называется первой ляпуновской величиной равновесия 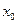. Бифуркационный смысл второго условия невырожденности станет ясен из дальнейшего.

Для данной бифуркации возможны две различные бифуркационные диаграммы, определяемые знаком U; они изображены на рис. 4.3. (Здесь и далее предполагается 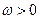, что всегда может быть получено заменой z на 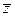) Независимо от знака 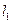положение равновесия z = 0 при переходе 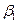через нуль теряет устойчивость, превращаясь из устойчивого фокуса при в неустойчивый при . Характер перестройки полных фазовых портретов в окрестности положения равновесия существенно зависит от знака 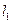. При 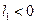потеря устойчивости фокуса сопровождается рождением малого устойчивого предельного цикла (рис. 4.3, а). В случае 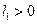потеря устойчивости фокуса связана с гибелью на нем неустойчивого предельного цикла (рис. 4.3, б). Этот цикл при ограничивает область притяжения устойчивого фокуса. Условие 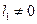обеспечивает рождение или гибель единственного предельного цикла.

С точки зрения приложений при 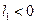устойчивый равновесный режим в изучаемой системе сменяется устойчивыми автоколебаниями малой амплитуды. Такая потеря устойчивости называется мягкой. В случае 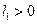после бифуркации устойчивый равновесный режим сменяется каким-то другим, сильно отличающимся от него, режимом: происходит жесткая потеря устойчивости.

Замечание. При бифуркационных значениях параметров положение равновесия устойчиво, если 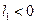, и неустойчиво, если 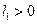. Устойчивость положения равновесия в критический момент определяет устойчивость рождающегося предельного цикла.

1 ТОПОЛОГИЧЕСКАЯ КЛАССИФИКАЦИЯ ГРУБЫХ ПОЛОЖЕНИЙ РАВНОВЕСИЯ

Различие между линеаризованной системой

y ˙ = Ay (1)

и исходной нелинейной системой

y ˙ = Ay + g (y) (2)

состоит в том, что интегрирование последней — задача, по сути, невыполнимая.

В связи с этим возникает естественный вопрос, который был впервые сформулирован Пуанкаре и Ляпуновым: «При каких условиях траектории системы (2) вблизи положения равновесия ведут себя аналогично траекториям линеаризованной системы (1)?»

В современной терминологии поведение двух систем называется аналогичным, если системы топологически эквивалентны.

Определение 2.2. Две n -мерные системы

y ˙ = Y ₁(y) и y ˙ = Y ₂(y),

определенные в областях D ₁ и D ₂, соответственно, топологически эквивалентны в подобластях U ₁ ⊆ D ₁ и U ₂ ⊆ D ₂, если существует гомеоморфизм

η: U ₁ → U ₂,

под действием которого при сохранении ориентации (направления движения) траектория (полутраектория, отрезок траектории) первой системы отображается в траекторию (полутраекторию, отрезок траектории) второй системы.

Подчеркнем также то, что вопрос об эквивалентности исходной нелинейной системы ее линеаризации в положении равновесия не имеет смысла, если на мнимой оси существует, по крайней мере, один характеристический показатель. То есть, системы не будут топологически эквивалентными, если положение равновесия негрубое. Этот факт иллюстрируется для систем на плоскости на двух приведенных ниже примерах.

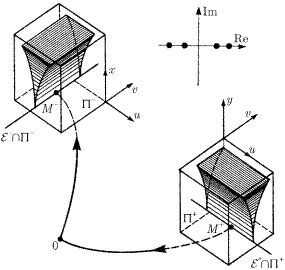
Рис. 1. Отображение вблизи седла в пространстве R⁴. Точка O имеет два собственных значения с положительными действительными частями и два — с отрицательными, то есть седло имеет двумерное устойчивое и двумерное неустойчивое подпространства

В первом случае положение равновесия имеет пару чисто мнимых показателей λ _{1 , 2} = ±iω ω > 0. Рассмотрим нелинейную систему

x ˙ = −ωy + g ₁(x, y),

y ˙ = ωx + g ₂(x, y), (3)

где предполагается, что функции g ₁ и g ₂, а также их первые производные обращаются в нуль в начале координат. Решение соответствующей линеаризованной системы в общем виде можно представить как

x = x ₀ cos(ωt) − y ₀ sin(ωt),

y = y ₀ cos(ωt) + x ₀ sin(ωt).

Здесь фазовые траектории являются замкнутыми кривыми (концентрическими окружностями), в центре которых лежит начало координат (рис. 1). Такое положение равновесия называется центром.

Фазовый портрет нелинейной системы в общем случае значительно отличается от рассмотренного выше. Например, если положить, что g ₁ = −x (x ² + y ²), а

g ₂= −y (x ²+ y ²), то решение уравнения (3) легко находится в полярных координатах:

r ² = 1/(2 t + r ₀^-2), ϕ = ωt + ϕ ₀.

В данном случае все траектории имеют форму спиралей, закрученных вокруг начала координат, как показано на рис. 2. Очевидно то, что в любых малых окрестностях обоих положений равновесия не существует гомеоморфизма, при помощи которого траектории такой системы отображаются в траектории линеаризованной системы (в связи с тем, что под действием гомеоморфизма замкнутые кривые отображаются в замкнутые кривые). Таким образом, данная система не является топологически эквивалентной ее линеаризации.

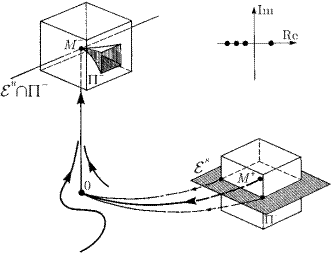
Рис. 2. Отображение вблизи седла в пространстве R⁴. Точка O — седло, имеющее трехмерное устойчивое подпространство Ɛ ^s и одномерное неустойчивое подпространство Ɛ ^u

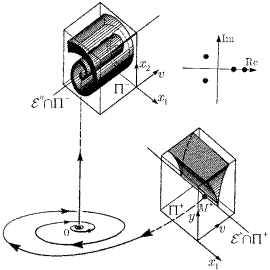
Рис. 3. Отображение вдоль траекторий, минующих седло-фокус (2,1). Отличие между отображениями состоит в размерности устойчивого и неустойчивого подпространств. Обратите внимание на расположение собственных значений

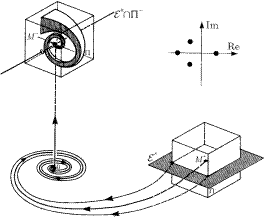
Рис. 4. Отображение вдоль траекторий, минующих седло-фокус (2,1). Отличие между отображениями состоит в размерности устойчивого и неустойчивого подпространств. Обратите внимание на расположение собственных значений

Во втором случае в положении равновесия один показатель λ ₁ равен нулю, а второй λ ₂ = −λ< 0. Данную систему можно записать в виде

x ˙ = g ₁(x, y),

y ˙ = −λy + g ₂(x, y), (4)

где функции g 1 и g 2, а также их первые производные обращаются в нуль в начале координат. Решение линеаризованной системы имеет вид

x = x ₀, y = e^−λty ₀ .

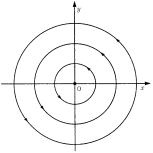
Рис. 5. Центр. В данном случае каждая траектория является концентрической окружностью, направленной против часовой стрелки

Фазовый портрет приводится на рис. 3. Ось x целиком состоит из положений равновесия линеаризованной системы, каждое из которых притягивает только пару траекторий. Очевидно, что нелинейная система может содержать континуум положений равновесия только при выборе строго определенных значений функций g ₁ и g ₂, следовательно, наличие топологической эквивалентности между исходной и линеаризованной системами в данном случае маловероятно.

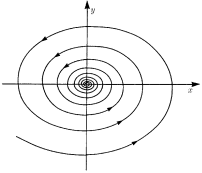
Рис. 6. Нелинейности вызывают изменение поведения траекторий вблизи центра. В данном случае траектории являются спиралями, закрученными вокруг точки O

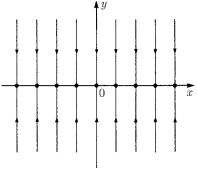
Рис. 7. Каждая точка на оси x является положением равновесия, притягивающим пару траекторий

На рис. 4 показан фазовый портрет в случае функций g ₁ = x ², g ₂ = 0. Из рисунков видно, что два локальных фазовых портрета не имеют ничего общего. Состояние равновесия, представленное на рис. 4, называется седло-узлом.

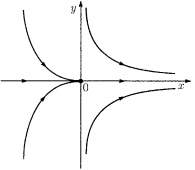
Рис. 8. Негрубая точка типа седло-узел. Точка O является устойчивой в области «узел» (x < 0), но неустойчивой в области «седло» (x > 0)

Задача топологической классификации грубых положений равновесия находит решение в следующей теореме:

Теорема 1.1 (Гробман – Хартман). Пусть точка O есть грубое положение равновесия. Тогда, существуют ее окрестности U ₁ и U ₂, в которых исходная и линеаризованная системы топологически эквивалентны.

Заметим, что положение равновесия нелинейной системы (2) в таком случае называют локально топологически эквивалентным положению равновесия ее линейной части (1).

В продолжение рассмотрения данной проблемы рассмотрим вопрос о топологической эквивалентности линейных систем. Определим топологический тип грубого положения равновесия как (k, n−k), где k — количество характеристических показателей, лежащих слева от мнимой оси, а (n − k) — справа от нее.

Теорема 1.2. Линейные системы с положениями равновесия одного типа топологически эквивалентны.

Доказательство этой теоремы конструктивно в том смысле, что гомеоморфизм η: R ⁿ → R ⁿ можно определить в явном виде. Например, рассмотрим две линейные системы, первая из которых в начале координат имеет фокус

x ˙ = −x + y,

y ˙ = −x – y (5)

а вторая — узел

x ˙ = −x,

y ˙ = − y /3. (6)

Эти системы топологически эквивалентны, так как при помощи гомеоморфизма

(x, y) → (x cos(τ) + y ³ sin(τ), y ³ cos(τ) − x sin(τ)),

где τ (x, y) = − ln(x ² + y ⁶) / 2, траектории системы (6) отображаются на траектории системы (5).

Непосредственно из теорем 1.1 и 1.2 следует очень важное заключение о том, что n-мерная система может иметь только (n + 1) различных топологических типов грубых положений равновесия. В частности, любая система с грубым положением равновесия типа (k, n−k) локально топологически эквивалентна системе

x ˙ = A_kx, (7)

где

,

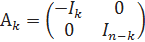Через I_i обозначена i -мерная единичная матрица. Если положить, что 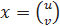, где u ∈ R ^k, v ∈ R ^n−k, то систему (7) можно представить в виде

u ˙ = −u,

v ˙ = v. (8)

Решение системы (8) задается при помощи выражений

u (t) = e^−Iktu ₀, v (t) = e^I(n−k)tv ₀. (9)

Если k = n, то при t → + ∞ все траектории системы (9) стремятся к положению равновесия в начале координат. Следовательно, согласно теоремам 1.1 и 1.2, любая траектория из достаточно малой окрестности положения равновесия типа (n, 0) нелинейной системы также стремится к положению равновесия при t → + ∞. Такое положение равновесия называется устойчивым топологическим узлом или стоком. Заметим, что на основании теоремы 1.2 все n -мерные устойчивые фокусы и узлы, рассмотренные в предыдущем разделе, топологически эквивалентны, а следовательно, являются стоками.

Любая траектория из малой окрестности положения равновесия O типа (0, n) стремится к точке O при t→−∞. При t → + ∞ любая траектория, за исключением точки O, покидает окрестность. Такое положение равновесия называется неустойчивым топологическим узлом или источником.

Остальные грубые положения равновесия называют топологическими седлами. Из теоремы Гробмана –Хартмана следует, что топологическое седло исходной нелинейной системы имеет локально устойчивое и локально неустойчивое многообразия W^s_loc и W^u_loc размерности k и (n − k), соответственно. То есть, если h — локальный гомеоморфизм, под действием которого траектории линеаризованной системы отображаются на траектории нелинейной системы (в данном случае такой гомеоморфизм существует согласно теореме 1.1), то образы h Ɛ ^s и h Ɛ ^u устойчивого и неустойчивого инвариантных подпространств линеаризованной системы как раз являются устойчивым и неустойчивым многообразиями. Аналогично линейному случаю, положительная полутраектория, выходящая из любой точки многообразия W^s_loc, лежит в нем полностью и стремится к положению равновесия O при t → + ∞. Подобным образом, отрицательная полутраектория, начинающаяся в любой точке многообразия W^u_loc, лежит в нем полностью и стремится к положению равновесия O при t→−∞. Траектории точек вне W^s_loc∪W^u_loc покидают любую окрестность седла при t→±∞. Многообразия W^s_loc и W^u_loc являются инвариантными, то есть они включают в себя все траектории (до тех пор, пока траектории остаются в некоторой окрестности топологического седла).

Очевидно, что если две системы X ₁ и X ₂ топологически эквивалентны, то при помощи гомеоморфизма, определяющего топологическую эквивалентность, положения равновесия системы X ₁ отображаются на положения равновесия системы X ₂. Если O ₁ — положение равновесия системы X ₁, а O ₂— образ O ₁ относительно гомеоморфизма, то траектория, асимптотическая к O ₁ при t → + ∞ (соответственно, t→−∞), отображается в траекторию, асимптотическую к O ₂ при

t → + ∞ (t → −∞). Следовательно, устойчивые (неустойчивые) многообразия локально топологически эквивалентных седел имеют равные размерности. Таким образом, приходим к теореме.

Теорема 1.3. Два грубых положения равновесия являются локально топологически эквивалентными тогда и только тогда, когда они принадлежат одному и тому же топологическому типу.

Топологический подход позволяет успешно решить задачу классификации грубых положений равновесия. Однако он не дает ответов на ряд важных вопросов, например, на вопрос об экспоненциальной скорости сходимости к положению равновесия, о характере такой сходимости (монотонная или осциллирующая сходимость), о гладкости инвариантных многообразий и т. д. Эти мельчайшие (то есть неразличимые посредством локальных гомеоморфизмов) подробности, касающиеся поведения траекторий вблизи положений равновесия крайне важны при изучении различных гомоклинических бифуркаций, играющих главную роль в динамических системах со сложной динамикой.

2 КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ ОДНОМЕРНЫХ И ДВУМЕРНЫХ СИСТЕМ

Исследование любого явления, проявляющего динамическое поведение, как правило, начинается с построения соответствующей математической модели динамической системы в виде (1.2.1).

1. ϕ (0, x) = x.

2. ϕ (t 1, ϕ (t 2, x)) = ϕ (t 1 + t 2, x). (1.2.1)

3. ϕ (t, x)непрерывно по(x, t).

Наличие модели в явном виде позволяет проследить эволюцию ее состояния при изменении t, поскольку исходные данные определяют единственное решение системы (1.2.1). Для полного изучения системы необходимо найти это решение, то есть «проинтегрировать. исходную систему». Интегрирование системы. подразумевает получение в качестве ее решения аналитического выражения. Однако данная цель достижима только для очень малого класса динамических систем: для систем линейных уравнений с постоянными коэффициентами и для некоторых особых уравнений, которые можно проинтегрировать в квадратурах. Вместе с тем, даже в случае, когда решение представлено в аналитическом виде, координатные функции, определяющие решение, могут быть настолько сложны, что непосредственный анализ становится практически невозможным. Кроме того, задача нахождения решения в аналитическом виде не является главной целью нелинейной динамики, которая, в основном, затрагивает «качественные» свойства такие, как количество положений равновесия, устойчивость, существование периодических траекторий и т. д. В частности, мы попытаемся описать важные качественные особенности этих функций путем геометрического представления фазовых траекторий. Вот почему данный метод называется «качественным интегрированием».

Качественное исследование включает два этапа:

- определение всех возможных типов траекторий, имеющих определенное поведение и «формы»;

- описание для каждой группы топологически схожих систем.

Первый этап довольно прост. По сути, его можно переформулировать следующим образом: необходимо определить, к чему стремится траектория при

t→ + ∞ (t→−∞). В этом случае мы должны положить, что траектория L, задаваемая уравнением x = ϕ (t), при t ≥ t ₀ (t ≤ t ₀) остается в некоторой ограниченной области фазового пространства. При изучении данного вопроса существенными являются следующие понятия.

Определение 1.3. Точку x^∗ называют ω -предельной точкой траектории L, если для некоторой последовательности {t_k}, где t_k → + ∞,

lim ϕ (t_k) = x^∗

k→∞

Аналогичное определение α -предельной точки применимо для t_k →−∞ при k → ∞. Обозначаем множество всех ω -предельных точек, принадлежащих траектории L, через Ω _L, а множество α -предельных точек —через А _L. Заметим, что положение равновесия представлено единственной предельной точкой. В случае, если траектория L — периодическая, все точки, принадлежащие ей, являются α и ω -предельными точками, то есть L = Ω _L = А _L. Если L — незамкнутая устойчивая по Пуассону траектория, то множества Ω _L и А _L совпадают с ее замыканием Ĺ. Множество Ĺ является либо минимальным (если L — рекуррентная траектория), либо квазиминимальным множество, если время возвращения Пуанкаре траектории L неограничено. Все положения равновесия, а также периодические и устойчивые по Пуассону траектории самопредельны.

Структура множеств Ω _L и А _L более подробно изучена для двумерных динамических систем, все траектории которых при t → ±∞ остаются в некоторой ограниченной области на плоскости. Для данного случая Пуанкаре и Бендиксон установили, что множество Ω _L можно представить лишь одним из трех приведенных ниже топологических типов:

I. Положения равновесия.

II. Периодические траектории.

III. Циклы, образованные положениями равновесия и траекториями, стремящимся к данным положениям равновесия при t→±∞.

На рисунке 1.3.1 приведены примеры предельных множеств типа III; положения равновесия обозначены через O. Используя указанную общую классификацию, можно перечислить все типы положительных полутраекторий систем на плоскости:

1) положения равновесия;

2) периодические траектории;

3) полутраектории, стремящиеся к положению равновесия;

4) полутраектории, стремящиеся к периодической траектории;

5) полутраектории, стремящиеся к предельному множеству типа III.

Аналогичная ситуация имеет место в случае отрицательных полутраекторий. Среди периодических траекторий двумерных систем особую роль играют траектории, представляющие собой ω - либо α -предельные множества незамкнутых траекторий, расположенных во внутренней или внешней области периодической траектории, как показано на рис. 1.3.2. В теории двумерных систем такая траектория называется предельным циклом.

Аналогичная ситуация для многомерных систем намного сложнее. В данном случае, помимо положений равновесия и периодических траекторий, предельные множества могут быть минимальными или квазиминимальными множествами различных топологических типов таких, как странные аттракторы, которые могут быть гладкими или негладкими многообразиями или фрактальными множествами с локальной структурой прямого произведения диска на канторово множество, и на другие еще более экзотические множества.

Вернемся к задаче, касающейся изучения совокупности траекторий. В сущности, описать динамическую систему означает дать топологическое (качественное) разбиение фазового пространства на области существования траекторий разных топологических типов. Эту задачу, как правило, называют «построение фазового портрета». При ее решении возникает вопрос: «В каком случае два фазовых портрета являются одинаковыми?» С точки зрения качественной теории динамических систем ответ на поставленный вопрос можно получить, вводя понятие топологической эквивалентности.

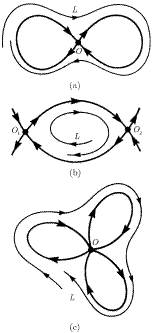
Рис. 1.3.1. Под буквами (a) и (c) приведены примеры двух ω -предельных гомоклинических циклов; под буквой (b) — пример гетероклинического цикла, образованного двумя траекториями, направленными от одного положения равновесия к другому

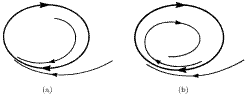
Рис. 1.3.2. (a) ω -предельный цикл. (b) Цикл, являющийся для незамкнутых траекторий в его окрестности как ω -, так и α -предельным

Определение 1.4. Две системы являются топологически эквивалентными, если существует гомеоморфизм соответствующих фазовых пространств, отображающий траектории одной системы в траектории второй.

В этом определении подразумевается, что положения равновесия, а также периодические и незамкнутые траектории одной системы соответственно отображаются в положения равновесия, периодические и незамкнутые траектории другой системы. Топологическая эквивалентность двух систем в некоторой области фазового пространства определяется аналогично. Последняя, как правило, используется для изучения локальных задач, например, в окрестности положения равновесия либо вблизи периодической или гомоклинической траектории. Определение топологической эквивалентности двух динамических систем дает косвенное определение качественной структуры разбиения фазового пространства на области существования траекторий различных топологических типов. Такие структуры должны быть инвариантны относительно всех возможных гомеоморфизмов фазового пространства.

Пусть G — ограниченная область фазового пространства, а H = {h_i} — множество гомеоморфизмов в G. Метрика задается следующим образом:

dist(h ₁, h ₂) = sup h ₁ x − h ₂ x.

x∈G

Определение 1.5. Траектория L (L ∈ G) называется особой, если при достаточно малом значении ε > 0 для всех гомеоморфизмов h_i, удовлетворяющих условию dist(h_i, I) < ε, где I — тождественное отображение, выполняется условие

h_iL = L.

Очевидно, все положения равновесия и периодические траектории являются особыми траекториями. Незамкнутые траектории также могут быть особыми. Например, все траектории двумерной системы, стремящиеся к положениям равновесия седлового типа как при t → + ∞, так и при t→−∞, являются особыми. Поскольку такие траектории разделяют определенные области на плоскости, их называют сепаратрисами (см. примеры сепаратрис, приведенные на рис. 1.3.1). Определение особых полутраекторий можно сформулировать аналогично.

Определение 1.6. Две траектории L ₁ и L ₂ эквивалентны, если при ε > 0 существуют такие гомеоморфизмы h ₁, h ₂ ,..., h_{m ( ε )}, что

L ₂ = h_{m ( ε )} · · · h ₁ L ₁.

где dist(h_k, I) < ε (k = 1, 2 ,...,m (ε)).

Каждое множество эквивалентных траекторий будем называть ячейкой. Заметим, что все траектории в ячейке имеют один и тот же топологический тип. В частности, если ячейка состоит из незамкнутых траекторий, то все они имеют одни и те же ω - и α -предельные множества. Особые траектории и ячейки особенно важны для двумерных систем. В этом случае можно определить некоторое множество S, если взять из каждой ячейки по одной траектории (все особые траектории по определению принадлежат S). Данное множество S будем называть схемой. Допустим, что множество S состоит из конечного числа траекторий.

Теорема 1.3. Схема является полным топологическим инвариантом.

Данная теория не только является математической основой теории колебаний двумерных систем, но также предоставляет методы исследования конкретных систем. В частности, исследование проводится в следующем порядке: сначала классифицируются положения равновесия, а затем все особые траектории, такие как сепаратрисы, стремящиеся к седловым положениям равновесия, и траектории, предельные для множеств типа III при t → + ∞ либо при t → −∞. Полный набор особых траекторий определяет схематический портрет, называемый скелетом. Он позволяет разделить фазовое пространство на ячейки и изучить поведение траекторий внутри каждой из них.

К сожалению, данный метод неприемлем для исследования многомерных систем. Множество особых траекторий в трехмерной системе может быть бесконечным или даже континуальным. То же самое относится к ячейкам. Таким образом, в этом случае задача нахождения полного топологического инварианта кажется не вполне реалистичной. Поэтому мы должны смириться с относительно неполной классификацией, основанной на некоторых топологических инвариантах, которые можно применить лишь в определенных случаях. Тем не менее, основной подход для изучения конкретных многомерных систем остается таким же, как и для двумерных: анализ системы начинается с исследования положений равновесия и периодических траекторий.

Рассмотрим двумерную систему (n=2).

При n = 2 общий вид системы следующий:

x ˙ = a ₁₁ x + a ₁₂ y,

y ˙ = a ₂₁ x + a ₂₂ y. (2.2.1)

Соответствующее характеристическое уравнение записывается как

λ ² − (a ₁₁ + a ₂₂) λ + (a ₁₁ a ₂₂ − a ₁₂ a ₂₁) = 0, (2.2.2)

а корни определяются выражением

λ _{1 , 2} = (a ₁₁ + a ₂₂) / 2 ± .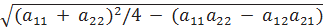

Пуанкаре первым дал названия основным положениям равновесия двумерных систем. В зависимости от характеристических показателей λ _{1 , 2} выделяются следующие типы положений равновесия:

1. λ ₁ и λ ₂ — действительные отрицательные: λ ₁ < 0 и λ ₂ < 0. Такое положение равновесия O называют устойчивым узлом. При λ ₁ ≠ λ ₂ систему (2.2.1) путем невырожденного линейного преобразования пространственных переменных можно привести к виду

ξ ˙ = λ ₁ ξ,

η ˙ = λ ₂ η (2.2.3)

где ξ (t) и η (t) — проекции фазовой точки (x (t), y (t)) на собственные векторы матрицы 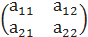, соответствующие собственным значениям λ ₁ и λ ₂. Решение системы (2.2.3) в общем виде определяется выражением

ξ = e^{λ 1 t}ξ ₀, η = e^{λ 2 t}η ₀. (2.2.4)

Поскольку значения λ _{1 , 2} отрицательны, все траектории притягиваются к началу координат при t → + ∞. Кроме того, каждая траектория достигает начала координат по касательной либо к оси ξ, либо к оси η. Чтобы проверить это, исследуем следующее уравнение интегральных кривых системы (2.2.3):

ηξ^ν ₀ = ξ^νη ₀ (2.2.5)

где ν = |λ ₂ |/|λ ₁ |. Для определенности допустим, что |λ ₂ | больше |λ ₁ |. Тогда ν > 1, и, согласно уравнению (2.2.5), все траектории достигают точки O по касательной к оси ξ, кроме двух траекторий, лежащих на оси η (рис. 2.2.1). Оси ξ и η называются ведущим и неведущим направлениями, соответственно.

При λ ₁ = λ ₂ = −λ < 0 систему (2.2.1) можно записать в следующем виде:

ξ ˙ = −λξ + η,

η ˙ = −λη (2.2.6)

(нетривиальный блок Жордана), или в виде

ξ ˙ = −λξ,

η ˙ = −λη. (2.2.7)

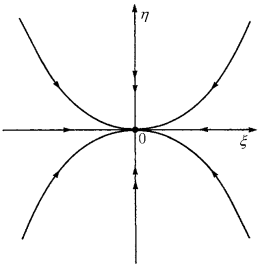
Рис. 2.2.1. Устойчивый узел. Двойными стрелками показано сильно устойчивое (неведущее) направление, совпадающее с осью η

Решение в общем виде системы (2.2.6) описывается следующими выражениями:

ξ = e^−λtξ ₀ + te^−λtη ₀, η = e^−λtη ₀ (2.2.8)

а системы (2.2.7) — выражениями

ξ = e^−λtξ ₀, η = e^−λtη ₀. (2.2.9)

На рис. 2.2.2 показан фазовый портрет, соответствующий первому случаю. Все траектории стремятся к точке O по касательной к единственному собственному вектору — оси ξ. Во втором случае любая траектория приближается к точке O в собственном направлении, как показано на рис. 2.2.3. Такой узел называется дикритическим.

2. Пара комплексно-сопряженных корней: λ _{1 , 2} = −ρ ±iω, где ρ > 0, ω > 0. В данном случае положение равновесия O называется устойчивым фокусом. При помощи невырожденной нелинейной замены координат систему (2.2.1) можно преобразовать следующим образом:

ξ ˙ = −ρξ − ωη,

η ˙ = ωξ − ρη. (2.2.10)

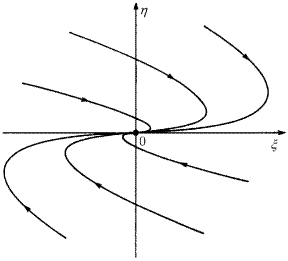
Рис. 2.2.2. Другой пример устойчивого узла. Каждая траектория приближается к началу координат в единственном ведущем направлении, совпадающем с осью ξ

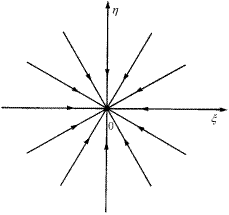
Рис. 2.2.3. Дикритический узел. Каждая траектория стремится к точке O в собственном направлении

При записи в полярных координатах ξ = r cos ϕ, η = r sin ϕ система (2.2.10) принимает вид

r ˙ = −ρr,

ϕ ˙ = ω. (2.2.11)

Решение системы (2.2.11) в общем виде можно представить при помощи уравнений

r (t) = e^−ρtr ₀,

ϕ (t) = ωt + ϕ ₀, (2.2.12)

или, возвращаясь к декартовым координатам, как

ξ (t) = e^−ρt (ξ ₀ cos(ωt) − η ₀ sin(ωt)),

η (t) = e^−ρt (ξ ₀ sin(ωt) + η ₀ cos(ωt)). (2.2.13)

Фазовый портрет показан на рис. 2.2.4. Любая траектория (за исключением O) имеет вид спирали, закрученной против часовой стрелки и стремящейся к началу координат при t → + ∞.

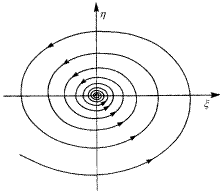
Рис. 2.2.4. Устойчивый фокус на плоскости

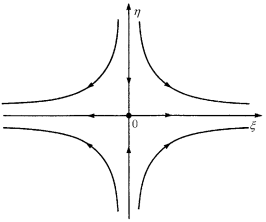
Рис. 2.2.5. Плоское седло

3. И λ ₁ и λ ₂ являются действительными числами, но имеют противоположный знак:

λ ₁ = γ > 0, λ ₂ = −λ < 0. Такая точка равновесия называется седлом. Линейная замена переменных приводит систему (2.2.1) к виду

ξ ˙ = γξ,

η ˙ = −λη. (2.2.14)

Решение системы (2.2.14) в общем виде можно представить при помощи уравнений

ξ = e^γtξ ₀, η = e^−λtη ₀. (2.2.15)

Соответствующее уравнение интегральных кривых имеет вид

ηξ^ν = ξ^ν ₀ η ₀, (2.2.16)

где ν = λ/γ. Портрет фазового пространства (или просто «фазовое пространство») вблизи седла показан на рис. 2.2.5. Существует четыре исключительные траектории, называемые сепаратрисами: две устойчивые и две неустойчивые, которые стремятся к седлу O при t → + ∞ и t → −∞, соответственно. Остальные траектории минуют седло. Пара устойчивых сепаратрис и седло O образуют устойчивое инвариантное подпространство (ось η). Неустойчивое инвариантное подпространство (ось ξ) состоит из неустойчивых сепаратрис и точки седлового типа.

4. Случай, когда действительные части обоих характеристических показателей положительны, легко сводится к рассмотренным выше случаям (1) и (2) путем обращения времени t→−t, в результате чего направление стрелок на соответствующем фазовом портрете меняется на противоположное. Если характеристические показатели — действительные числа, то соответствующее положение равновесия называется неустойчивым узлом. В случае комплексных характеристических показателей его называют неустойчивым фокусом (см. рис. 2.2.6 и 2.2.7).

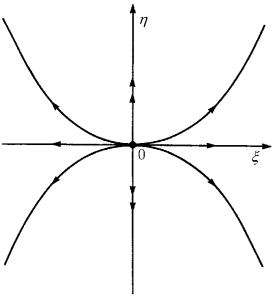
Рис. 2.2.6. Неустойчивый узел. Фазовый портрет получен в соответствии с рис. 2.2.1 путем обращения времени

3 ПОНЯТИЕ ПОРЯДКА И ХАОСА В ДИНАМИЧЕСКИХ СИСТЕМАХ

В реальной природе протекает множество хаотических процессов, но мы не воспринимаем их как хаос, и наблюдаемый мир кажется нам вполне стабильным. Наше сознание, как правило, интегрирует, обобщает информацию, воспринимаемую органами чувств, и поэтому мы не видим мелких «дрожаний» – флуктуаций – в окружающей нас природе. Самолет надежно держится в воздушных турбулентных вихрях, и хотя они неупорядочено пульсируют, подъемную силу самолета можно рассчитать с точностью до нескольких килограммов как некоторую среднюю величину. Из далекого космоса на Землю приходят сигналы от спутников и космических объектов, и из гигантского моря хаотических помех удается «выловить» нужную информацию. Собственно, вся радиофизика строится на «разбраковке» по определенным статистическим закономерностям полезных данных и вредных «шумов».

Как показывает пример турбулентности, поведение нелинейной системы трудно предсказать – она «отзывается» на возмущение своего состояния весьма сложным образом и, как правило, неоднозначно. Поэтому, чтобы исследовать нелинейные процессы, обычно приходится использовать так называемый «принцип линеаризации», то есть сводить нелинейную систему с присущим ей неоднозначным откликом к линейной, которая характеризуется вполне «надежным» предсказуемым поведением. По существу, это – кардинальное упрощение и тем самым загрубление сути явления.

Но на наших глазах технический прогресс сопровождается появлением все более сложных систем, например, в энергетике, и то, как гарантировать устойчивость их работы, полное отсутствие непредсказуемых сбоев, становится все более важной задачей. Сегодня потребовались новые подходы, принципиально новый взгляд на проблему анализа нелинейных процессов, приводящих к непрогнозируемому поведению, к «хаосу». И хотя сущность порядка и хаоса до сих пор не сформулирована, в последние годы появилась надежда разобраться в действии механизмов непредсказуемости, включая переходы «порядок – хаос» либо «хаос – порядок» (такие переходы и их двунаправленность обозначают П↔Х).

Сначала о порядке

Порядок в физической, экологической, экономической и любой другой системе может быть двух видов: равновесный и неравновесный. При равновесном порядке, когда система находится в равновесии со своим окружением, параметры, которые ее характеризуют, одинаковы с теми, которые характеризуют окружающую среду; при неравновесном порядке они различны.

В физике самый главный из них – температура: никакое равновесие невозможно, если внутри рассматриваемой нами системы температура не такая, как у окружения. При этом сразу возникают тепловые потоки, начинается перетекание тепла от горячих тел к холодным, которое будет продолжаться до тех пор, пока температура не установится на едином для всех тел – как в системе, так и ее окружении – уровне. Другой важный параметр, характеризующий физическую систему, – давление. При равновесном порядке давление внутри системы должно быть равно давлению на нее со стороны окружения. Экономические и социальные системы тоже описываются обобщающими параметрами, которые при равновесии принимают фиксированные значения.

На первый взгляд равновесный порядок более «стабилен», чем неравновесный. В самой природе равновесного порядка заложено противодействие любым возмущениям состояния системы (такое «упрямство» в термодинамике называется принципом Ле-Шателье).

Способность возвращаться к исходному состоянию – непременное свойство так называемых саморегулирующихся систем. И хотя «саморегулирование» – термин сравнительно недавний, возник он, по существу, вместе с кибернетикой, саморегулирующиеся процессы встречаются в природе сплошь и рядом.

Природа неравновесного порядка другая. Этот вид порядка – искусственного происхождения и, как мы уже говорили, существует только при условии подачи энергии (или питательной массы) извне. Действительно, ведь неравновесность – неодинаковость параметров системы и среды – вызывает потоки тепла и массы. Поэтому для поддержания порядка требуется компенсировать потери, к которым приводят необратимые «выравнивающие» потоки. Другими словами, нужны энергетические затраты. Если подпитку энергией прекратить, то система «свалится» в состояние равновесного порядка. Потери, связанные с перетеканием тепла или массы, называются диссипативными, поскольку их физическая сущность – рассеяние энергии, как говорят, ее диссипация. Создается парадоксальная ситуация: в условиях диссипации, традиционно воспринимаемой как проявление распада структур, их неустойчивости, возникает порядок.

Мы редко задумываемся над тем, что человеческий организм существует в состоянии неравновесного порядка, когда энергетические потери компенсируются за счет энергии топлива (пищи) и окислителя (воздуха). Когда же жизненный путь организма заканчивается, он переходит в состояние полного равновесия с окружающей средой (равновесный порядок).

Физика – наука количественная, и, чтобы получить конкретный результат, нужно перейти от общих рассуждений к уравнениям и математическим образам. Самым полезным из таких образов, с помощью которого можно изобразить ход процесса, состояние системы и степень ее организованности, оказалось так называемое фазовое пространство. Координатами в этом пространстве служат различные параметры, характеризующие рассматриваемую систему. В механике, например, это положения и скорости всех точек, движение которых мы рассматриваем, и поэтому в современной аналитической механике фазовое пространство, пожалуй, основное понятие.

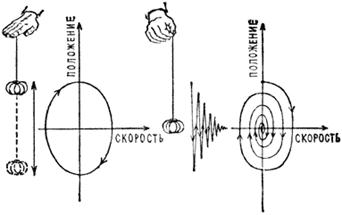
Рис. 2.

Фазовое пространство – это, с одной стороны, абстрактное математическое пространство, координатами в котором служат положения и скорости всех точек физической системы, а с другой стороны, оно очень удобно для наглядного описания ее эволюции. Например, движение шарика на абсолютно упругой резинке, в которой нет трения, полностью определяется начальной скоростью и положением шарика (начальными условиями). Каждому мгновенному состоянию такого осциллятора – колебательной системы – отвечает точка на фазовой плоскости. Когда шарик колеблется вверх и вниз без трения, эта точка описывает замкнутую кривую, а если колебания постепенно затухают, то фазовая траектория сходится по спирали к предельной точке, соответствующей остановке шарика. Эта точка неподвижна: если шарик подтолкнуть, его фазовая кривая вернется в ту же точку, которая как бы притягивает все близлежащие траектории. Поэтому ее называют неподвижной притягивающей точкой, или фокусом. Такая притягивающая точка – простейший тип аттрактора.

Что же дает изображение процессов в фазовом пространстве? А вот что: только взглянув на «фазовый портрет» физической системы, мы можем заявить, находится она в состоянии равновесного или неравновесного порядка. Более того, несмотря на их разную физическую сущность, эти два вида порядка можно изобразить на одной и той же диаграмме в виде четких точек, линий и фигур. Можно также нарисовать диаграмму перехода из одного упорядоченного состояния в другое.

А всегда ли геометрические образы на фазовой диаграмме будут четкими? Оказывается, что существует класс явлений, противоположных порядку как по физической сущности, так и по характеру изображения на фазовой диаграмме. Их образы размыты, нечетки, носят случайный, или, как говорят, стохастический характер. Явления, порождающие такие образы, называются хаотическими.

Что такое «хаос»?

Обычно под хаосом всегда понималось неупорядоченное, случайное, непрогнозируемое поведение элементов системы. Многие годы господствовала теория, утверждавшая, что статистические закономерности определяются только числом степеней свободы: полагали, что хаос – это отражение сложного поведения большого количества частиц, которые, сталкиваясь, создают картину неупорядоченного поведения. Наиболее характерный пример такой картины – броуновское движение мелких частиц в воде. Оно отражает хаотические тепловые перемещения громадного числа молекул воды, случайным образом ударяющих по плавающим в воде частицам, вынуждая их к случайным блужданиям. Такой процесс оказывается полностью непредсказуемым, недетерминированным, поскольку точно установить последовательность изменений в направлении движения частицы невозможно – мы ведь не знаем, как движутся все без исключения молекулы воды. Но что отсюда следует? А вот что: становится невозможным вынести такие закономерности, которые позволяли бы точно прогнозировать каждое последующее изменение траектории частицы по предыдущему ее состоянию. Иными словами, не удается надежно, достоверно связать между собой причину и следствие или, как выражаются специалисты по математической физике, формализовать причинно-следственные связи. Такой вид хаоса можно назвать недетерминированным (НХ). И все же некоторые усредненные характеристики поведения в состоянии недетерминированного хаоса были найдены. Используя аппарат статистической физики, ученые сумели вывести формулы, описывающие кое-какие обобщенные параметры броуновского движения, например, расстояние, пройденное частицей за некоторое время (первым эту задачу решил А. Эйнштейн).

Однако в самые последние годы внимание исследователей все больше сосредоточилось на так называемом детерминированном хаосе (ДХ). Этот вид хаоса порождается не случайным поведением большого количества элементов системы, а внутренней сущностью нелинейных процессов. (Именно такой хаос и привел к энергетической катастрофе в Нью-Йорке.) Оказывается, что детерминированный хаос – отнюдь не редкость: всего два упруго сталкивающихся бильярдных шара образуют систему, сложная поведенческая функция которой имеет статистические закономерности, то есть содержит элементы «хаоса». Отталкиваясь друг от друга и от стенок бильярдного стола, шары рассеиваются под разными углами, и через некоторую последовательность соударений их можно рассматривать как неустойчивую динамическую систему с непрогнозируемым поведением. Аналитические решения нелинейных уравнений, описывающих поведение таких систем, как правило, не могут быть получены. Поэтому исследования проводятся с помощью вычислительного эксперимента: на ЭВМ шаг за шагом получают численные значения координат отдельных точек траектории.

В фазовом пространстве детерминированный хаос отображается непрерывной траекторией, развивающейся во времени без самопересечения (иначе процесс замкнулся бы в цикл) и постепенно заполняющей некоторую область фазового пространства. Таким образом, любую сколь угодно малую зону фазового пространства пересекает бесконечно большое количество отрезков траектории. Это и создает в каждой зоне случайную ситуацию – хаос: И вот что удивительно: несмотря на детерминизм процесса – ведь бильярдные шары полностью подчиняются классической, «школьной» механике, – ход его траектории непредсказуем. Другими словами, мы не в состоянии предвидеть или хотя бы грубо охарактеризовать поведение системы на достаточно большом отрезке времени и в первую очередь потому, что принципиально отсутствуют аналитические решения.

Порядок на сковородке

Если налить на сковороду тонкий слой какой-нибудь вязкой жидкости (например, растительного масла) и нагревать сковороду на огне, поддерживая температуру масляной поверхности постоянной, то при слабом нагреве – малых тепловых потоках – жидкость остается спокойной и неподвижной. Это типичная картина состояния, близкого к равновесному порядку. Если сделать огонь побольше, увеличивая тепловой поток, то через некоторое время – совершенно неожиданно – вся поверхность масла преображается: она разбивается на правильные шестигранные или цилиндрические ячейки. Структура на сковороде становится очень похожей на пчелиные соты. Это замечательное превращение называется явлением Бенара, по имени французского исследователя, одним из первых изучившего конвективную неустойчивость жидкости.

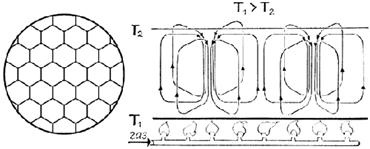
Рис. 3. Конвективные ячейки Бенара.

Конвективные ячейки Бенара

В 1900 году была опубликована статья французского исследователя Бенара с фотографией структуры, по виду напоминавшей пчелиные соты. При нагревании снизу слоя ртути, налитой в плоский широкий сосуд, весь слой неожиданно распадался на одинаковые вертикальные шестигранные призмы, которые впоследствии были названы ячейками Бенара. В центральной части каждой ячейки жидкость поднимается, а вблизи вертикальных граней опускается. Иными словами, в сосуде возникают направленные потоки, которые поднимают нагретую жидкость (с температурой T ₁) вверх, а холодную (с температурой T ₂) опускают вниз.

Если и дальше увеличивать тепловой поток, то ячейки разрушаются – происходит переход от порядка к хаосу (П→Х). Но самое удивительное заключается в том, что при еще больших тепловых потоках наблюдается чередование переходов:

Х→П→Х→П→...!

При анализе этого процесса в качестве параметра, который показывает, когда на сковороде будет «порядок» и когда «хаос», то есть определяющего «зону» порядка или хаоса, выбирается так называемый критерий Рэлея, пропорциональный разности температур вверх по слою масла. Этот параметр называют управляющим, поскольку он «управляет» переводом системы из одного состояния в другое. При критических значениях Рэлея (математики называют их точками бифуркации) и наблюдаются переходы «порядок – хаос».

Нелинейные уравнения, которыми описывается образование и разрушение структур Бенара, называются уравнениями Лоренца. Они связывают между собой координаты фазового пространства: скорости потоков в слое, температуру и управляющий параметр.

Процессы, происходящие в сосуде, могут быть зафиксированы, например, киносъемкой и сопоставлены с результатами вычислительного эксперимента. На рис. 4 показано именно такое сопоставление. Совпадение результатов физического и вычислительного экспериментов поразительно! Но прежде, чем перейти к анализу этих результатов, нам придется еще раз обратиться к фазовому пространству.

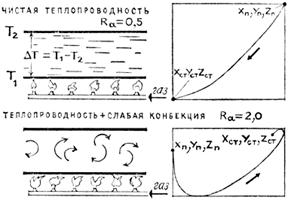
Рис. 4а. Переходы от порядка к хаосу на примере явления Бенара.

Переходы от порядка к хаосу на примере явления Бенара.

Управляющим параметром, который играет роль «ручки регулировки», здесь служит так называемый критерий Рэлея (Re), пропорциональный разности температур вверх по слою жидкости. «Вращение» этой регулирующей ручки соответствует большему или меньшему нагреву жидкости. При слабом нагреве (Re < 1) в слое нет конвективных потоков, и динамическая система, образом которой служит изображающая точка в фазовом пространстве, стремится к состоянию равновесного порядка. С увеличением разности температур между сковородкой и внешней поверхностью жидкости (Re ≈ 1) возникают малые конвективные токи. Это состояние соответствует неравновесному порядку.

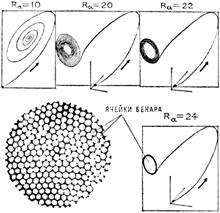
Рис. 4б.

«Вращая» дальше ручку регулировки (Re ≈ 10...20), мы приходим к неравновесному порядку с аттрактором типа устойчивого фокуса – это в вычислительном эксперименте, на экране дисплея или на графопостроителе. А в физическом эксперименте отчетливо наблюдаются ячейки Бенара.

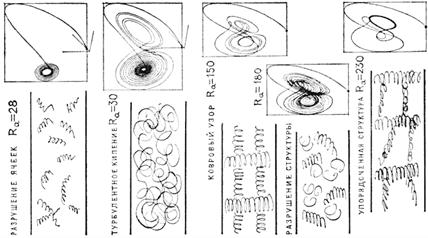
Рис. 4в.

Интересна динамика процесса с ростом числа Рэлея. Расстояния между «оборотами» фазовой траектории (их обычно называют ветвями) постепенно сокращаются, и в конце концов изменяется характер аттрактора – фокус переходит в предельный цикл, который потому и называется предельным, что служит пограничной кривой между зонами устойчивости и неустойчивости; теперь даже при очень малом увеличении управляющего параметра начинают образовываться турбулентные вихри. Порядок переходит в хаос. В вычислительном эксперименте возникает неустойчивый фокус, а затем появляется странный аттрактор. В физическом эксперименте ячейки Бенара разрушаются, этот процесс напоминает кипение.

Почему фазовое пространство оказалось таким мощным средством для изучения хаоса? Прежде всего потому, что оно позволяет представить поведение нелинейной, «хаотической» системы в наглядной геометрической форме. Так, поведение большинства нелинейных систем в фазовом пространстве определяется некоторой зоной в нем, называемой аттрактором (от английского to attract – притягивать). В эту зону в конечном итоге «притягиваются» траектории, изображающие ход процесса.

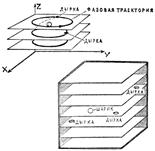
Рис. 5.

Странный аттрактор – абстрактное понятие, введенное для описания хаотического состояния. Универсального и наглядного образа странного аттрактора, к сожалению, не существует. Можно, однако, сконструировать детскую игрушку, представляющую собой многослойный лабиринт (трехмерное фазовое пространство), по которому бегает шарик (изображающая точка). В плоскостях между слоями имеются дырки, натыкаясь на которые шарик проваливается вниз. Однако

Дата добавления: 2014-01-07