Сертификационная оценка устойчивости самоходного скрепера

Жесткая, единая конструкция какого-либо тягача, находящегося на опорной поверхности, теряет устойчивость в том случае, когда равно­действующая внешних сил выходит за пределы опорного контура [24]. Опорный контур определяется многоугольником, замыкающим внеш­ние опоры конструкции, а каждая прямая, соединяющая смежные опо­ры, может стать ребром опрокидывания. Для шарнирно-сочлененных конструкций самоходных скреперов с одноосным тягачом это условие. устойчивости недостаточно, так как в этом случае между двумя жест­кими телами (тягач и полуприцепная секция скрепера) имеется шар­нир с двумя степенями свободы. Наличие такого шарнира допускает отрыв от опорной поверхности какого-либо одного колеса одной из секций при последующем касании с опорной поверхностью высту­пающих частей другой секции. При этом тягач, находящийся в поло­жении поворота относительно скреперного ковша, может опрокиды­ваться вперед (рис. 34, а), с отрывом от опоры внешнего по повороту колеса, или назад (рис. 34, б), с отрывом от опоры внутреннего по по­вороту колеса полуприцепной секции. Направление опрокидывания

зависит от направления действия опрокидывающих нагрузок, от вели­чины и направления склона опорной поверхности.

Статическая устойчивость

Самоходные машины с одноосными тягачами обладают более вы­сокой статической устойчивостью в положении прямолинейного дви­жения, чем в положении поворота. При этом величины предельных значений критического угла складывания в_кр и угла склона (З_пр взаи­мосвязаны. При этих углах продолжение "контактной линии" колес тя­гача (прямой, соединяющей центры "пятен контакта" колес тягача) проходит через центр "пятна контакта" одного из колес полуприцепной секции машины. В этом положении машина рассматривается с точки зрения устойчивости как единая конструкция с ребром опрокидывания, проходящим через точки контакта с опорой колес тягача и одного из колес полуприцепной секции машины (линия ОК на рис. 35). Рассмот­рим сначала условие опрокидывания тягача вперед по его ходу со­гласно расчетной схеме (рис. 35, а), где стрелкой показано направле­ние склона. Предельный угол склона и критический угол складывания при повороте тягача взаимосвязаны

tgj3_np=[(Bsine_Kp-r_ncos0_Kp)(1-k)-r_Tk]/H, (1)

где

^{1 D}

k=G_T/(G_T+G_n);

H - высота общего центра тяжести, м;

/ - смещение шарнира сцепного устройства от колесной оси тягача, м;

D - расстояние от шарнира сцепного устройства до колесной оси полуприцепа, м;

В - половина колеи полуприцепа, м;

Гт- расстояние от колесной оси тягача до его центра тяжести, м;

г_п - расстояние от колесной оси полуприцепа до его центра

тяжести, м;

Gt-вес тягача, кН;

Ь_п - вес полуприцепа, кН.

В случаях, когда центр тяжести тягача или полуприцепа находится за соответствующими колесными осями (назад по ходу машины), ко­ординаты Гт и г_п в формулу (1) подставляются с обратным знаком.

Для расчета предельного угла склона при опрокидывании назад (рис.35, б) критический угол складывания принимают равным 90°, так как положение с углом складывания более 90° не обеспечивается кон­струкцией механизма поворота скрепера, что обеспечивает запас ус­тойчивости. Ребром опрокидывания в расчете принимают линию ОК, проходящую через центральную точку "пятна контакта" внешнего по повороту колеса полуприцепа и точку пресечения проекции горизон­тальной оси шарнира сцепного устройства с контактной линией колес тягача.

tgj3'_np=[(B sin(p'_Kp-r_ncos(p'_Kp)(1-k)+ r_Tk sin<p'_Kp]/H, (2)

где J3'_np - предельный угол склона в статике при опрокидывании тя­гача назад;

<р'кр- угол между колесной осью полуприцепа и линией ОК (рис.35, б),

<р'_кр = arctg D/(B+I).

Рис. 34. Опрокидывание самоходной машины с одноосным тягачом: а - вперед; б - назад

Расчет статической устойчивости ведется для четырех расчетных случаев: для опрокидывания тягача вперед и назад с грузом и без гру­за в ковше скрепера.

Рис. 35. Схемы машины в расчетных положениях:

а - при опрокидывании вперед;

б - при опрокидывании назад

Динамическая устойчивость

В процессе маневрирования на машину действуют центробежные силы и силы инерции при разгоне и торможении. Наиболее опасным является динамический опрокидывающий момент, возникающий при торможении машины, движущейся в повороте с критическим углом складывания. При торможении под действием инерционных сил ма­шина может начать опрокидывание, вращаясь относительно ребра опрокидывания ОХ (рис. 36, а). Одновременно она некоторое время продолжает вращаться вокруг центра поворота в плане. В зависимо­сти от величины замедления и времени его действия процесс опроки­дывания может закончиться до выхода проекции общего центра тяже­сти за пределы ребра опрокидывания, и тогда система возвращается в исходное положение (в противном случае машина теряет устойчи-

вость). Тягач при этом, наклоняясь вперед, передним брусом подмо-торной рамы опускается на дорогу, а внешнее (по повороту) колесо полуприцепа отрывается от опоры и поднимется вверх (см. рис. 34, а).

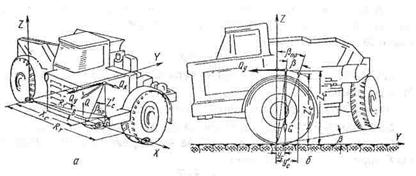
Рис.36.Схема сил, действующих на машину при торможении в повороте: а - до начала опрокидывания; б - в процессе опрокидывания

Дифференциальное уравнение движения анализируемой системы относительно оси X (рис. 36, а)

Т 'Л Л Г ИГ Г\

I_x-J3+M_G-M_D=0

где /_х - момент инерции системы тягач-полуприцеп относительно оси X;

Р - угловое ускорение;

Мв - восстанавливающий момент от сил тяжести; Мо - опрокидывающий динамический момент. Восстанавливающий момент от сил тяжести

M_G=Gy_c.

Координата центра тяжести системы у_с в процессе опрокидывания машины относительно оси X будет изменяться в зависимости от угла поворота /3

y_c=y\fiosfi-ZcSinfi, где у_с и z_c - координаты центра тяжести системы относительно осей у и z при р=0 (т.е. до начала опрокидывания). Тогда получим M_G=G(y'_ccosj3 - z'csinp) Опрокидывающий момент Мо создается при торможении машины за счет силы инерции Q, действующей в горизонтальной плоскости, проходящей через центр тяжести системы. Направление действия этой силы перпендикулярно к радиусу R_c поворота относительно оси z центра тяжести машины.

M_D-=Q_yz_c, где Q_y=Q cos<5 - составляющая силы Q, перпендикулярная к реб­ру опрокидывания (оси X);

S- угол между радиусом поворота центра тяжести и осью X; z_c ⁼ ycSinfi + z_ccos(3 - координата центра тяжести по оси Z Сила инерции Q при постоянной за время действия тормозной си­лы F определится выражением

Q=mFR_TRc/l_z, где т - масса системы;

Rt- условный радиус точки приложения силы F относительно цен­тра поворота;

/_z - момент инерции системы относительно оси Z, который при по­вороте системы относительно оси X изменяется в зависимости от угла Р по закону

\₂ - l_ysin²p+l'_zcos²p-ispSmBcosji, где /_у и \_г -моменты инерции системы относительно осей Y и Z до начала опрокидывания;

lyz - центробежный момент инерции системы относительно плоско­сти VOX до начала опрокидывания.

Приняв обозначение x_c=R_cCOsS, получим M_D=mFR_TXc(ycSinp + z'_ccosfi)/(I _ysin²p+l _zcos²p -lyzSinficosfi). Подставив полученные значения Mq и Mq в исходное уравнение движения системы в процессе опрокидывания, получим

1_хр + G(y'cCOsj3 -z _csinp)-mFR_TXc(y cSinp + +z'_ccosp)/(l'ySin²p+l'₇cos²p -l'yzSinpcosp)=0

Учитывая, что угол /? находится практически в пределах 0°...20°, принимают COSfi^1,sinfi~j3, тогда

I ySin²р+12.cos²p -lyzSinficosp ж / _z. Ошибка от такой замены не превышает 6% и, кроме того, пойдет в запас устойчивости. После упрощения и замены

F/W/_Z=a_c получим

/;/+ G(y_c -2ф)-та_с(Ус13 + г_с)=0. Решение этого уже линейного уравнения имеет вид

/?=С)е^ю+с₂е"^к'-рЖ², где

p=(ma_cz'c-Gy'_c)/l_x, K²=(ma_cy_c+Gzc)/I_x. Процесс опрокидывания рассматривают как двухэтапный: от мо­мента начала торможения до его окончания и после окончания дейст­вия торможения. Общее решение дифференциального уравнения для обоих этапов будет одинаковым. Изменятся только постоянные коэф­фициенты Ci и Сг, определяемые при рассмотрении начальных усло­вий: для первого этапа ti=0, /?/=0, Д=0, для второго этапа tu=0,

Рн-fh, Р~Рт, где (Зт и Вт- угол и угловая скорость опрокидывания в конце первого этапа.

В результате имеем для первого этапа

0FP(chKt, - 1)/К², /3i=(pshKti)/K, j3_T=p(chKt_T - 1)/К², /3_T=(pshKt_T)/K _:

для второго этапа

(iirpTishKi tu)/^ +y'o/'z_c - (y'c/z'c -/Зт) chKi t„,

(31г13т(с1г)К4н) - My Л с -fflshKitu,

где

\Gz

¥ — £_

Дата добавления: 2014-01-07