Уравновешивание одной массы

Расчетное уравновешивание неуравновешенных вращающихся масс расположенных в одной плоскости

Имеем звено, в котором на расстоянии от оси вращения l ₁ располагается неуравновешенная масса m ₁ (рис. 10.2). В общем случае звено может вращаться с переменной скоростью, т. е. кроме угловой скорости ω будет иметь место угло­вое ускорение ε. В результате действуют две силы инерции: центробежная Р _и1 и касательная Р ^τ₁.. Каждая из этих сил будет восприниматься опорой О. Модули этих сил соответственно равны: 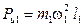, 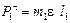. Уравновесим вначале силу Р _и1 введя дополнительную массу т на расстоянии l по линии действия силы Р _и1.

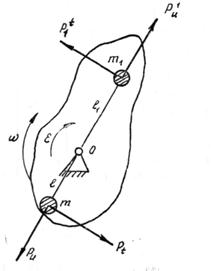
Рис. 10.2. Уравновешивание одной массы

Условие уравновешивания

Р _и1+ Р _и = 0. (10.1)

Подставив в уравнение (10.1) значение сил и сократив полученное после подста­новки уравнение на общий множитель ω², получим

m ₁ l ₁ + ml = 0. (10.2)

Это и будет условие уравновешивания силы Р _и1.

Следовательно, для того чтобы уравновесить центробежную силу, необходимо при­ложить дополнительную массу таким образом, чтобы сумма статиче­ских моментов дополнительной массы и неуравновешенной массы относительно оси вращения равнялась нулю.

С приложением до­полнительной массы т возникает не только центробежная сила P _и, но и касательная сила, равная по модулю P^t = m ε l.

Условие (8.2) умножим на ε, тогда векторная сумма m₁εl₁ + mεl = 0 или

Р ^τ₁ + Р ^τ = 0. Это есть условие равновесия касательных сил.

Следовательно, условие уравновешивания центробежных сил (10.2) вместе с тем является и условием уравновешивания касательных сил, т. е. полным условием уравновешивания массы т₁. Значит, при уравновешивании масс необходимо уравновешивать центробежные силы инерции, касательные же силы инерции будут уравновешиваться автоматически. Поэтому в дальнейшем будем рассматривать только центробежные силы инерции.

Дата добавления: 2014-01-07