Логическая модель представления знаний

В основе моделей такого типа лежит формальная система, задаваемая четверкой вида: М = < Т, Р, А. В >. Множество Т – это множество базовых элементов. Например, это могут быть слова из какого то ограниченного словаря или детали конструктора. Для множества Т существует некоторый способ определения принадлежности или непринадлежности произвольного элемента к этому множеству. Процедура такой проверки может быть любой, но за конечное число шагов она должна давать ответ на вопрос, является ли х элементом множества Т или нет.

Множество Р – это множество синтаксических правил. С их помощью из элементов множества Т образуют синтаксически правильные совокупности (СПС). Например, из слов словаря строятся синтаксически правильные фразы, из деталей конструктора собираются новые механизмы. Существует процедура, с помощью которой за конечное число шагов можно определить, является ли совокупность Х синтаксически правильной.

В множестве синтаксически правильных совокупностей выделяется некоторое подмножество А. Элементы множества А называются аксиомами. Аксиомы составляют ядро предметной области. Существует процедура, с помощью которой для любой СПС можно получить ответ на вопрос является ли она аксиомой.

Множество В – это множество правил вывода. Применяя их к элементам множества А, можно получать новые СПС, к которым снова можно применять правила из множества В. Так формируется множество выводимых в данной формальной системе совокупностей. Если имеется процедура, с помощью которой можно определить для любой СПС, является ли она выводимой, то такая формальная система называется разрешимой. Правила вывода являются самой сложной частью логической модели.

В логической модели знаний можно считать, что множества А образует все единицы знаний, которые введены в базу знаний извне, а с помощью правил вывода из них выводятся новые производные знания. Формальная система представляет собой генератор порождения новых знаний, образующий множество выводимых в данной системе знаний. Это свойство логических моделей позволяет хранить в базе лишь те знания, которые образуют множество А, а все остальные знания из них получать по правилам вывода.

На практике логическая модель чаще всего используется в системе логики предикатов и выведения заключений с помощью силлогизмов. Предикатом или логической функцией называется функция от любого числа аргументов, принимающих истинное значение И(1) и Л(0). Аргументы принимают значения из произвольного конечного или бесконечного множества М, называемого предметной областью. Предикат от n аргументов является n-мерным предикатом.

Силлогизм – это заключение. С помощью силлогизмов из двух суждений выводится третье. Например:

- все металлы электропроводны;

- медь – металл. Заключение – медь электропроводна.

Отличительными чертами логических моделей является единственность толкования и возможность реализации системы точных определений и выводов.

Формальные логические модели, основанные на исчислении предикатов, используются как один из методов представления знаний в ИИ, не используемых, как правило, в промышленных ИС.

В любом языке для создания языковых форм должно быть определено следующее; множество знаков, которые можно в нем использовать; полное определение слов через знаковые последовательности; грамматические правила образования предложений из слов (семантические правила).

Каждое слово из предложения соответствует объектам и действиям того реального мира, который описывается этим языком. Таким образом, в языке присутствуют слова, которые описывают сущности, и слова, которые описывают атрибуты сущностей и действия над ними.

Для формулировки знаний о некоторой предметной области средствами логики предикатов в проблемной области выделяют два основных типа констант:

- дискретные объекты, которые называют сущностями;

- отношения между сущностями.

Именам отношений соответствуют термы определений, а сущностям – аргументы. Символы, используемые для обозначения высказываний, называются атомами. Интерпретацией формулы называется приписывание каждому атому, входящему в формулу, истинностного значения. Таблицей истинности формулы называется таблица, содержащая истинностные значения формулы при всех возможных комбинациях истинностных значений входящих в нее атомов.

Логический вывод (силлогизм) в классической логике строится двумя путями: дедукцией и индукцией. В современной логике вывод строится также абдукцией. Индукция и абдукция называются вероятностными силлогизмами.

Дедукция – вывод, позволяющий получать заключение из большой или малой посылки. Большая посылка называется дедуктивным правилом, малая – фактическим заявлением (декларацией). Пример: Большая посылка: рыба – живое существо, умеющее плавать. Малая посылка: карась – рыба. Вывод: карась – живое существо, умеющее плавать.

Большая и малая посылки называются данными о знаниях или просто знаниями и их объем должен быть достаточно большим. Упорядоченное множество таких знаний и есть база знаний.

Дедуктивное правило позволяет детализировать и формализовать причинно-следственные связи явлений (процессов) и предметов, т. е. Это знания, необходимые для выполнения алгоритма принятия решений. Основная часть знаний кодируется не только арифметическими, но и логическими символами, т. е. требуется специальный язык для ЭВМ.

Индукция – получение большой посылки из заключения ее малой посылки. Можно ли считать правомерным определение «рыба – это живое существо, умеющее плавать» в качестве большой посылки, исходя из того, что известны многие виды рыб? Вывод неправомерен, т. к. Могут быть неизвестные виды рыб, перемещающиеся по суше. По мере накопления наблюдений повышается достоверность большой посылки.

Абдукция – получение малой посылки из заключения и большой посылки. На основании факта, что некоторые из живых суще6ств умеют плавать, делается заключение, что это живое существо – рыба. Однако этот вывод нельзя считать безусловно достоверным. Человек в обыденной жизни имеет постоянное дело с нечеткими, вероятностными оценками.

Все операции исчисления высказывания переносятся в исчисления предикатов и используются для связывания предикатов и формул, т. е. позволяют получить из простых выcказываний сложные.

Основные операции алгебры логики:

1. 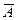– отрицание. Высказывание истинно, если высказывание А – ложно. если А – истинно.

2. (А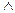В) – конъюнкция или логическое умножение (А и В). Высказывание истинно только том случае, если истины А и В.

3. (АВ) – дизъюнкция или логическое сложение (А+В). Высказывание истинно только в том случае, если истинно хотя бы одно из слагаемых.

4. (А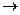В) импликация или следование В из А. Читается также «если А, то В». Высказывание ложно только в том случае, если А истинно и В ложно.

5. (А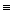В) – эквивалентность «А тогда и только тогда, когда В». Истинно тогда и только тогда, когда А и В имеют одно и то же истинное значение.

Таким образом основными операторами, образующими функции, соответствуют символы: - не (отрицание), - или (дизъюнкция), - и (конъюнкция), - следует (если, то), - импликация эквивалентно, логические связки.

В логике предикатов для компактной записи высказываний типа «для любого х истинно F(х)» и «существует такое х, для которого истинно F(х)» дополнительно вводятся две операции – квантор общности и квантор существования Вышеприведенные высказывания можно записать в следующем виде:

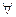xF(x) - высказывание истинно когда F(х) истинно для всех x € M и ложно в противоположном случае.

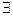xF(x) - высказывание истинно, когда существует элемент x € M, для которого F(х) истинно и ложно – в противоположном случае.

В логике предикатов обычно используются 6 типов символов:

- предметные переменные x, y, z, u, v, w или те же буквы с индексами;

- константы a, b, c, d, e или те же буквы с индексами;

- функциональные символы f, q, r,s,t или те же буквы с индексами;

- предикатные символы p, q, r, s, t или те же буквы с индексами;

- символы алгебры логики - ¬, , ,;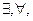

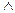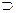- вспомогательные символы – круглые скобки и т. п.

Вывод, дающий заключение из двух посылок, можно представить следующим образом:

Предпосылка 1. - все металлы электропроводны;

Предпосылка 2.- медь – металл.

Заключение – медь электропроводна.

Если вместо имен субъектов подставить переменные x, y, то можно получить логическую формулу:

Предпосылка 1. 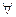x металл (x) электропроводен (x)

Предпосылка 2. металл (медь)

Заключение электропроводна (медь).

Логика предикатов рассматривает вопросы, можно ли, представляя предложения в логических формулах с помощью выводов получить из нескольких логических формул некоторую конечную логическую формулу.

Таким образом, в логике предикатов основным объектом исследования является формула. При ее определении используется понятие «терм» (некоторая сущность), объединяющая названия элементарных функций, к которым применима предикатная буква. Терм определяется следующим образом:

- всякая предметная переменная или константа являются термами;

- если f – n-местная функция из n предметов и t₁….t_n – термы, то f(t₁….t_n) есть терм.

Выражение р( t₁….t_m), где р предикатный символ m аргументов и t₁….t_m – термы называется атомарной функцией или атомом.

Атом и всякие выражения из них есть правильно построенные формулы (ППФ).

Пример: Предпосылка 1 (логическая формула) 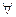x (р(х) q(x)

Предпосылка 2 (атом) р(а)

Заключение (атом) q(a)

Здесь р – металл, q – электропроводность, а – медь.

Интерпретация. Формула имеет определенный смысл, т. е. обозначает определенное высказывание, если существует какая-либо интерпретация. Интерпретировать формулу – значит связать с ней определенное множество М, т. е. конкретизировать предметную область, называемую также областью интерпретации и указать соответствие относящееся:

- каждой предметной константе в формуле конкретный элемент из М;

- каждой n-местной функциональной букве в формуле конкретную n-местную функцию на М;

- каждой n-местной предикатной букве в формуле конкретное отношение между n элементами из М.

Иными словами – интерпретирование формул исчисления предикатов – это конкретизация предметной области М и соответствия между символами, входящими в формулы с одной стороны, и элементами, функциями и отношениями на М с другой.

Пример: элементарная формула G(f(a,b), g(a,b))

Интерпретация: М – множество действительных чисел. а и в – числа 2, 3 соответственно;

f – функция сложения f(a,b) = (a+b); g – функция умножения g(a,b) = (a*b); G – отношение «не меньше».

Формула обозначает высказывание «сумма 2+3 не меньше произведения 2*3». Результат – ложь или 0. Если изменить интерпретацию, в=1 или в=2, то результат – истина.

Другая формула при той же интерпретации:

G(fg(x,x), g(y,y), g(a,g(x,y)))

Формула обозначает высказывание x² + y² > 2xy

Высказывание верно при любых х и у из М и всегда истинно.

Для описания высказываний на языке предикатов в заданной предметной области часто для обозначения предикатных букв и констант используются слова или сокращения, которые являются названиями определяемых ими свойств, отношений, объектов.

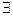(х) [Дельфин(х) умный (х)]

Дельфин наделен умственными способностями.

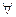(x) [Слон(х)→цвет (х, серый)]

Все слоны имеют серую окраску.

Область применения – для решения сравнительно простых задач.

Достоинства логических моделей – ясная семантика, возможность использования развитых механизмов логического вывода.

Одним из наиболее удобных средств поиска логического вывода является метод резолюций. Он заключается в том, что вместо заданной формулы рассматривается ее отрицание и доказывается противоречивость этой формулы.

Дата добавления: 2014-01-07