ЧАСТЬ 4. Формула полной вероятности. Формула Байеса

Систему событий называют полной группой событий, если выполняются условия: 1) ; 2) при . Это значит, что события полной группы попарно несовместны и в результате каждого испытания должно обязательно появляться одно из событий . Обозначим P(A_i)=p_i, тогда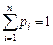

Другой пример. Проводится опыт, состоящий в бросании игральной кости. Пусть ─ событие, заключающееся в выпадении 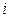очков на верхней грани этой кости, тогда события 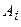− попарно несовместны ( при ) и в результате опыта обязательно должно появиться одно из событий 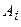(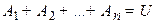). 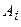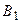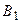Значит, события составляют полную группу событий, чего нельзя сказать о событиях − появление герба на первой монете и − появление цифры на второй монете в опыте, состоящем в одновременном подбрасывании двух монет (этому мешает хотя бы совместность событий и ).

Формула полной вероятности является следствием теорем сложения и умножения вероятностей.

Пусть некоторое событие А происходит только с каким-нибудь одним из событий Н₁, Н₂, Н₃, …, Н_n, которые образуют полную группу событий и называются гипотезами. В этом случае событие А можно представить в виде: А=А×Н₁ + А×Н₂ + А×Н₃ + … +А×Н_n. Отсюда, применяя теоремы сложения и умножения вероятностей и учитывая, что гипотезы попарно несовместны, получим:

(**)

которая называется формулой полной вероятности. Используя формулы (*) и (**), можно получить формулу Байеса (формулу вероятности гипотез):

События полной группы H₁, H₂, …H_n обычно называют гипотезами. Их вероятности были известны до проведения опыта.

Пример. В районе имеется три кинотеатра. Вероятность того, что Света пойдет в первый кинотеатр, равна 0,5; во второй – 0,3; в третий – 0,2. Вероятность встретить Ирину в одном из этих кинотеатров равна соответственно 0,7; 0,5 и 0,3. Света пошла в кино. Найти вероятность того, что она встретит Ирину.

Решение: Обозначим А – событие, состоящее в том, что Света встретит Ирину в кинотеатре; Н₁ – встреча состоялась в первом кинотеатре, Н₂ -во втором, Н₃ – в третьем. Из условия задачи известны: Р(Н₁)=0,5; Р(Н₂)=0,3; Р(Н₃)=0,2, а также 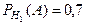, , 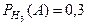. По формуле полной вероятности имеем:

Р(А) = 0,5×0,7 + 0,3×0,5 + 0,2×0,3 = 0,56.

Пример. Данные из предыдущего примера. Известно, что Света встретила Ирину в одном из кинотеатров. Найти вероятность того, что встреча состоялась в первом кинотеатре.

Решение: Используя полученные выше результаты, по формуле Байеса находим: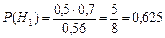

Пример. Три экзаменатора принимают экзамен по некоторому предмету у группы в 30 человек, причем первый опрашивает 6 студентов, второй — 3 студентов, а третий — 21 студента (выбор студентов производится случайным образом из списка). Отношение трех экзаменаторов к слабо подготовившимся различное: шансы таких студентов сдать экзамен у первого преподавателя равны 40%, у второго — только 10%, у третьего — 70%. Найти вероятность того, что слабо подготовившийся студент сдаст экзамен.

Решение. Обозначим через гипотезы, состоящие в том, что слабо подготовившийся студент отвечал первому, второму и третьему экзаменатору соответственно. По условию задачи

, , .

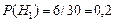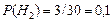Пусть событие A={слабо подготовившийся студент сдал экзамен}. Тогда снова в силу условия задачи

, , .

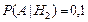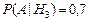По формуле полной вероятности получаем:

.

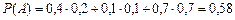Пример. Данные из предыдущего примера. Пусть известно, что студент не сдал экзамен, т.е. получил оценку «неудовлетворительно». Кому из трех преподавателей вероятнее всего он отвечал?

Решение. Вероятность получить «неуд» равна 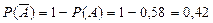. Требуется вычислить условные вероятности. По формулам Байеса получаем:

, и аналогично,

,

.

Отсюда следует, что, вероятнее всего, слабо подготовившийся студент сдавал экзамен третьему экзаменатору.

Пример. Была проведена одна и та же контрольная работа в трех группах. В первой группе из 30 студентов 8 выполнили работу на «отлично», во второй, где 28 студентов, – 6 «отличных» работ, в третьей, где 27 студентов, – 9 работ выполнены на «отлично». Найти вероятность того, что первая выбранная наудачу работа из работ, принадлежащих группе, которая также выбрана наудачу, окажется «отличной».

Решение: Имеем три гипотезы: H₁ – выбрана работа из 1-й группы, H₂ – выбрана работа из 1-й группы, H₃ – выбрана работа из 1-й группы. Очевидно, что

Обозначим искомое событие A – выбрана работа, выполненная на «отлично». Определим по классической формуле условные вероятности:

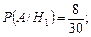
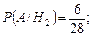
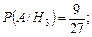
Отсюда по формуле полной вероятности

Пример. В группе из 10 студентов, пришедших на экзамен, 3 студента подготовлены отлично, 4 - хорошо, 2 - удовлетворительно и 1 - плохо. В экзаменационных билетах имеется 20 вопросов. Отлично подготовленный студент может ответить на все 20 вопросов, хорошо подготовленный - на 16, удовлетворительно подготовленный - на 10, плохо подготовленный - на 5. Вызванный наугад студент ответил на все три заданных преподавателем вопроса. Найти вероятность того, что этот студент: а) подготовлен отлично; б) подготовлен плохо.

Решение. Пусть событие А={студент ответил все три вопроса}. Введем систему гипотез:

H₁={студент подготовлен отлично};

H₂ ={студент подготовлен хорошо};

H₃={студент подготовлен удовлетворительно};

H₄ ={студент подготовлен плохо}.

Находим вероятности гипотез:

P(H₁) = 0,3; P(H₂) = 0,4; P(H₃) = 0,2; P(H₄) = 0,1.

Находим условные вероятности события А.

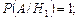
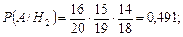
По формуле Байеса находим:

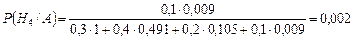
Ответ: 0,58; 0,002.

ЧАСТЬ 5. Схема решения задач по теории вероятности.

1. Прежде чем перейти к определению вероятности с помощью теорем о сложении и умножении вероятностей проверьте нельзя ли использовать классическое или геометрическое определение вероятности.

2. Определите не идет ли в задаче речь о ситуациях с полной группой событий (применяем формулу полной вероятности) или и о вероятности гипотез (применяем формулу Байеса).

3. Определить главное событие вероятность, которого требуется найти по условию задачи.

4. Определить составные события, как составные части главного события.

5. Определить связь между составными событиями: «И», «ИЛИ».

6. Если связь – «И», можно применять теоремы для произведения событий.

7. Если связь – «ИЛИ», можно применять теоремы для суммы событий.

8. При применении теоремы для произведения событий необходимо проверить события на зависимость и применять соответствующую теорему.

9. При применении теоремы для суммы событий необходимо проверить события на совместимость и применять соответствующую теорему.

Дата добавления: 2014-01-07