
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Механико-математические модели термоупруго/вязкопластических и упруго/вязкопластических тел
|
|
|
|
Вообще говоря, реальные материалы в той или иной степени обладают всеми тремя характерными механическими свойствами — упругими, вязкими и пластическими. Их проявление зависит от тех условий, при которых тело находится, и типа нагружения. Так, например, наличие температурного поля влияет на механические свойства тела. С ростом температуры тепловые колебания атомов усиливаются и облегчается активация механизма вязкопластического течения материала, т.е. тело проявляет в более сильной форме свои вязкие и пластические свойства. При динамическом нагружении также облегчается активация микромеханизма вязкопластических деформаций, и в этом случае тела имеют резко выраженный вязкопластический характер.
Для описания названных свойств особо подходящими являются модели, основанные на термодинамике тела с внутренними параметрами состояния. Эти параметры подбираются так, чтобы при их помощи можно было описывать на макроуровне пластическое и вязкое поведение тела. Определяющие уравнения для тел такого типа, вообще говоря, будут иметь вид  Вместе с тем нужно задать вид функции удельной свободной энтальпии
Вместе с тем нужно задать вид функции удельной свободной энтальпии 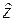 и уравнение для
и уравнение для 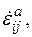 , зависящее от уравнений эволюции внутренних параметров состояния.
, зависящее от уравнений эволюции внутренних параметров состояния.
Наличие вязких свойств приводит к существенной зависимости механического поведения тела от времени (тело проявляет ползучесть, релаксирует и т.д.). Наличие пластических свойств вызывает появление остаточных деформаций и структурных изменений в теле. У одних материалов вязкие свойства проявляются в значительной степени еще при малых напряжениях и деформациях задолго до достижения предела текучести материала. У других материалов вязкие свойства проявляются вместе с пластическими за пределом текучести при статическом нагружении. Имеются материалы, у которых нет четко выраженного предела текучести, и все три типа свойств проявляются еще в области малых напряжений и деформаций. Это разнообразие проявления свойств является причиной построения различных механико-математических моделей тел; некоторые из них будут рассмотрены ниже.
Широкая группа материалов до достижения условия текучести материала при статическом нагружении (так называемого статического условия текучести) проявляет главным образом упругие и термоупругие свойства. При превышении этого предела развиваются вязкопластические деформации, при которых свойства тела становятся функциями времени и возникают необратимые структурные изменения материала. Для кристаллических тел микромеханизм вязкопластического деформирования связан с движением дислокаций в определенных на- правлениях. Их движению способствуют усиленные тепловые колебания атомов. У высокомолекулярных полимерных тел этот тип деформаций связан с химической реакцией распада, приводящей к разрыву связей полимерных цепей, образованию более низкомолекулярного полимера и образованию множества субмикротрещин. Эти вязкопластические свойства материала на макроуровне можно описать посредством тензора второго ранга 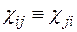 (внутреннего параметра состояния), связанного с плотностью соответствующего типа микродефектов в структуре материала. Если, кроме того, материал обладает свойством пластического упрочнения, то его можно описать посредством параметра пластического упрочнения
(внутреннего параметра состояния), связанного с плотностью соответствующего типа микродефектов в структуре материала. Если, кроме того, материал обладает свойством пластического упрочнения, то его можно описать посредством параметра пластического упрочнения 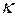 , также связанного с плотностью микродефектов в единице объема тела. При такой системе внутренних параметров состояния скорость неупругого деформирования
, также связанного с плотностью микродефектов в единице объема тела. При такой системе внутренних параметров состояния скорость неупругого деформирования  выражается следующим образом:
выражается следующим образом:
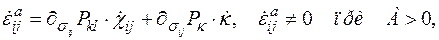 (1.1)
(1.1)
где

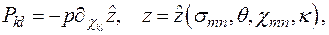 (1.2)
(1.2)
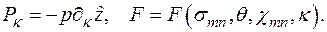
Здесь 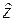 и
и  — функции состояния системы. Условие
— функции состояния системы. Условие  представляет собой статическое условие неупругого деформирования материала. Для вязкопластического деформирования бесконечно малой окрестности данной точки тела необходимо, чтобы состояние элементарной области к этой точке удовлетворяло условию
представляет собой статическое условие неупругого деформирования материала. Для вязкопластического деформирования бесконечно малой окрестности данной точки тела необходимо, чтобы состояние элементарной области к этой точке удовлетворяло условию 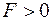 . Путем задания частого вида уравнений эволюции параметров
. Путем задания частого вида уравнений эволюции параметров  и
и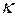 и выбора функций
и выбора функций 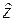 и F можно получить различные механико-математические модели. Эти уравнения можно представить в виде
и F можно получить различные механико-математические модели. Эти уравнения можно представить в виде
 при F> 0, (1.3)
при F> 0, (1.3)
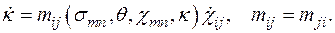
При помощи (1.3) равенство (1.1) преобразуется к виду
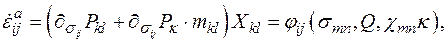 (1.4)
(1.4)
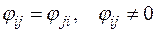 при F>0.
при F>0.
Вид зависимостей  определяется выбором функций
определяется выбором функций  и
и  Имеется ряд вязкопластических теорий, в которых используются функции
Имеется ряд вязкопластических теорий, в которых используются функции  различного типа. Выбор этих функций основан на экспериментальных результатах, полученных для реальных материалов с вязкопластическими свойствами рассматриваемого типа. Предложена и получила дальнейшее развитие модель вязкопластического тела на основе следующих предположений.
различного типа. Выбор этих функций основан на экспериментальных результатах, полученных для реальных материалов с вязкопластическими свойствами рассматриваемого типа. Предложена и получила дальнейшее развитие модель вязкопластического тела на основе следующих предположений.
а) Существует функция состояния F, зависящая от параметров состояния 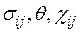 и
и 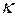 такая, что F= 0 является условием неупругого деформирования материала при статическом нагружении.
такая, что F= 0 является условием неупругого деформирования материала при статическом нагружении.
б) Скорость неупругого деформирования материала  для тех точек тела, для которых
для тех точек тела, для которых  не равна нулю. Эта скорость тем больше, чем больше значение функции
не равна нулю. Эта скорость тем больше, чем больше значение функции  в рассматриваемой точке.
в рассматриваемой точке.
в) Считается, что при изотермической деформации выполняется постулат устойчивости Друккера для неупругих материалов. В силу этого постулата, если к телу, находящемуся под действием определенной системы поверхностных и объемных сил, приложить некоторое дополнительное нагружение, то работа, совершаемая этой дополнительной системой сил, является положительной. Если при помощи дополнительных сил осуществить полный цикл нагружения и разгрузки, то они в течение этого цикла совершают неотрицательную работу. Постулат устойчивости материала выделяет класс материалов, для которых малым внешним изменениям нагружения соответствуют малые изменения внутри тела. Этот постулат можно записать в виде
 (1.5)
(1.5)
где  и
и 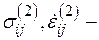 напряжения и скорости деформации, соответствующие двум состояниям тела в процессе дополнительного изменения нагрузки, протекающего в интервале времени
напряжения и скорости деформации, соответствующие двум состояниям тела в процессе дополнительного изменения нагрузки, протекающего в интервале времени  Если рассмотреть замкнутый цикл напряжений (приложение и снятие дополнительного нагружения) и начать с такого напряженного состояния
Если рассмотреть замкнутый цикл напряжений (приложение и снятие дополнительного нагружения) и начать с такого напряженного состояния  для которого
для которого 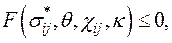 то ему будет соответствовать скорость неупругой деформации
то ему будет соответствовать скорость неупругой деформации  Ввиду обратимости упругой части деформации, при замкнутом цикле упругая часть мощности обратится в нуль и (1.5) примет вид
Ввиду обратимости упругой части деформации, при замкнутом цикле упругая часть мощности обратится в нуль и (1.5) примет вид
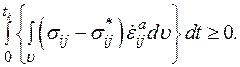 (1.6)
(1.6)
Работа неупругой деформации совершается не в течение всего прo-цесса  а только в интервале времени
а только в интервале времени  которому в пространстве напряжений соответствует область, расположенная выше поверхности
которому в пространстве напряжений соответствует область, расположенная выше поверхности  . Если применимость постулата распространить от всего тела на любую бесконечно малую окрестность точек тела, то из (1.6) получается условие Друккера о локальной устойчивости материала
. Если применимость постулата распространить от всего тела на любую бесконечно малую окрестность точек тела, то из (1.6) получается условие Друккера о локальной устойчивости материала
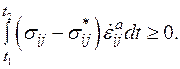 (1.7)
(1.7)
Рассматривая малый интервал времени  и разлагая (1.7) в ряд Тейлора в окрестности момента времени
и разлагая (1.7) в ряд Тейлора в окрестности момента времени 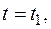 получим неравенства постулата Друккера о локальной устойчивости неупругого материала во времени
получим неравенства постулата Друккера о локальной устойчивости неупругого материала во времени
 (1.8)
(1.8)
и
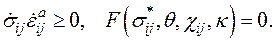 (1.9)
(1.9)
Из этих неравенств, как и в случае пластически деформируемых материалов, следует, что статическое условие неупругого течения  в пространстве напряжений изображает выпуклую поверхность и вектор скорости неупругой деформации ортогонален к ней при фиксированных
в пространстве напряжений изображает выпуклую поверхность и вектор скорости неупругой деформации ортогонален к ней при фиксированных  и
и 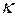 .
.
г) Материал является неупруго несжимаемым, т.е. 
д) Пластические и вязкие характеристики материала зависят от температуры.
После этих предположений функция  принимает вид
принимает вид
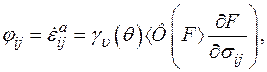 (1.10)
(1.10)
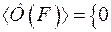 при
при 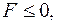
 при
при 
В (1.10)  —коэффициент вязкости, зависящий от температуры
—коэффициент вязкости, зависящий от температуры  . Функция
. Функция 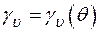 для некоторых материалов экспериментально определена. Функция Ф описывает вязкопластические свойства материала и также определяется экспериментально. Для этой функции, исходя из аналитической аппроксимации экспериментальных результатов, чаще всего применяют степенную или экспоненциальную зависимость, т.е. полагают
для некоторых материалов экспериментально определена. Функция Ф описывает вязкопластические свойства материала и также определяется экспериментально. Для этой функции, исходя из аналитической аппроксимации экспериментальных результатов, чаще всего применяют степенную или экспоненциальную зависимость, т.е. полагают 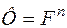 или
или 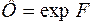 и т.д.
и т.д.
Как видно из (1.6), тензор  пропорционален градиенту
пропорционален градиенту  что является следствием предположения (в). Предположение (г) требует независимости
что является следствием предположения (в). Предположение (г) требует независимости  от первого инварианта тензора напряжений. Из предположения (б) следует, что
от первого инварианта тензора напряжений. Из предположения (б) следует, что  должна быть возрастающей функцией
должна быть возрастающей функцией 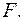 В качестве условий неупругого деформирования при статическом нагружении
В качестве условий неупругого деформирования при статическом нагружении  можно принять различные условия текучести. Чаще всего применяют условие типа
можно принять различные условия текучести. Чаще всего применяют условие типа
 (1.11)
(1.11)
Если ввести понятие об активных напряжениях, т.е. положить 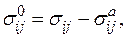 то условие (1.11) приводится к виду
то условие (1.11) приводится к виду
 (1.12)
(1.12)
где  тензор микронапряжений, который в случае упругопластических тел совпадает с
тензор микронапряжений, который в случае упругопластических тел совпадает с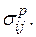 Можно использовать также
Можно использовать также  .
.
При помощи условия типа Мизеса соотношения (1.12) принимают вид
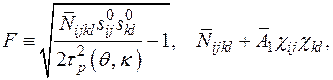 (1.13)
(1.13)
где 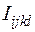 — единичный изотропный тензор четвертого ранга с постоянными компонентами,
— единичный изотропный тензор четвертого ранга с постоянными компонентами, 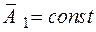 , а
, а  — предел текучести при чистом сдвиге и статическом нагружении, являющийся, вообще говоря, функцией параметра упрочения
— предел текучести при чистом сдвиге и статическом нагружении, являющийся, вообще говоря, функцией параметра упрочения 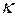 и абсолютной температуры
и абсолютной температуры  . Если неупругая деформация вызывает изменение условия неупругого деформирования кинематического типа, условие (1.13) принимает вид
. Если неупругая деформация вызывает изменение условия неупругого деформирования кинематического типа, условие (1.13) принимает вид
 (1.14)
(1.14)
Для неупруго сжимаемых материалов, например грунтов и др., предположение (г) неприменимо. Для них предполагают, что  вообще говоря, является функцией всех трех инвариантов тензора напряжений.
вообще говоря, является функцией всех трех инвариантов тензора напряжений.
Если условие неупругого деформирования относится к изотропному типу, тогда  не будет зависеть от
не будет зависеть от  и (1.14) преобразуется следующим образом:
и (1.14) преобразуется следующим образом:
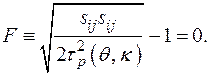 (1.15).
(1.15).
Если отсутствует пластическое упрочнение, то  не будет зависеть от
не будет зависеть от 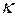 и
и  Часто вместо параметра внутреннего состояния
Часто вместо параметра внутреннего состояния  в качестве внутреннего параметра состояния используется сама неупругая деформация
в качестве внутреннего параметра состояния используется сама неупругая деформация 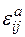 . В этом случае можно использовать приведенные выше формулы, заменяя в них
. В этом случае можно использовать приведенные выше формулы, заменяя в них  на
на 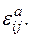 Зависимость (1.10) дает основание считать, что скорость неупругой деформации имеет потенциал и функция
Зависимость (1.10) дает основание считать, что скорость неупругой деформации имеет потенциал и функция 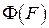 удовлетворяет условию Липшица, т.е.
удовлетворяет условию Липшица, т.е.
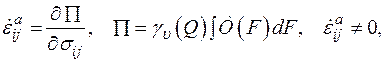 при F>0. (1.16)
при F>0. (1.16)
Некоторые авторы для скорости неупругой деформации вводят непосредственно выражение вида (1116). При этом существование потенциальной функции П определяют ее характер и обосновывает при помощи микроструктурного анализа механизм вязкопластической деформации. Эти теории строятся на основе следующих предположений.
а) Материалы кристаллической структуры состоят из монокристаллов, в которых имеются определенные кристаллографические направления скольжения. При скольжении обе части кристалла перемещаются одна относительно другой. В монокристалле имеется определенное число систем скольжения. Любая система скольжения состоит из параллельных плоскостей, для которых имеется фиксированное направление скольжения.
б) В зависимости от ориентации кристалла по отношению к внешнему воздействию и его величины скольжение будет иметь место в одной или нескольких системах, если приведенное напряжение в соответствующем направлении превысит определенное значение (т.е. считается, что к монокристаллам применим закон Шмидта).
в) Скольжение имеет место вследствие перемещений дислокаций. Дислокации как линейные дефекты кристаллической структуры вызывают внутренние напряжения. Чтобы возникло перемещение дислокаций и вместе с ним скольжение в определенной системе, необходимо преодолеть, с одной стороны, межатомные силы, а с другой, силы противодействия со стороны других дефектов. В макромасштабе преодоление этих сил проявляется как превышение статического условия текучести в некоторой бесконечно малой окрестности рассматриваемой точки. Тепловая активация атомов облегчает передвижение дислокаций.
При этих допущениях скорость неупругой деформации монокристалла выражается формулой
 (1.17)
(1.17)
где 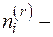 единичный нормальный вектор r-ой системы скольжения, а
единичный нормальный вектор r-ой системы скольжения, а  единичный вектор направления скольжения этой системы,
единичный вектор направления скольжения этой системы, скорость относительного перемещения двух параллельных плоскостей r-ой системы, находящихся на расстоянии, равном единице. В случае вязкопластической деформации скорость
скорость относительного перемещения двух параллельных плоскостей r-ой системы, находящихся на расстоянии, равном единице. В случае вязкопластической деформации скорость  определяется выражением вида
определяется выражением вида
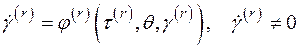 при
при 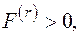 (1.18)
(1.18)
где 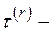 приведенное касательное напряжение (
приведенное касательное напряжение (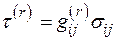 ). Функция
). Функция  при
при 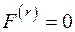 служит условием осуществления скольжения в r-ой системе, т. е.
служит условием осуществления скольжения в r-ой системе, т. е.

где m — число всех механизмов. Суммирование в (1.17) ведется по всем активным механизмам (r). Данный механизм является активным, если для него 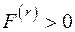 или
или  при
при  (т.е. когда приведенное касательное напряжение в направлении скольжения r-й системы превышает соответствующее предельное значение). При определенных условиях — малых скоростях деформации и умеренных температурах — в этих выражениях можно перейти к случаю пластического тела. Согласно теориям скольжения, пластическая деформация является частным случаем более общего типа вязкопластической деформации тел. В рассматриваемом случае параметры
(т.е. когда приведенное касательное напряжение в направлении скольжения r-й системы превышает соответствующее предельное значение). При определенных условиях — малых скоростях деформации и умеренных температурах — в этих выражениях можно перейти к случаю пластического тела. Согласно теориям скольжения, пластическая деформация является частным случаем более общего типа вязкопластической деформации тел. В рассматриваемом случае параметры  играют роль внутренних параметров состояния с уравнениями эволюции (1.18). Уравнение (1.17) можно записать через потенциальную функцию, если ввести функции
играют роль внутренних параметров состояния с уравнениями эволюции (1.18). Уравнение (1.17) можно записать через потенциальную функцию, если ввести функции
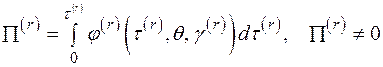 при
при 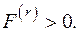 (1.19)
(1.19)
С их помощью для монокристалла вводится потенциальная функция П:
 (1.20)
(1.20)
причем суммирование производится по всем активным механизмам 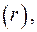 для которых
для которых 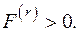 Тогда при помощи (1.20) уравнение (1.17) приводится к виду
Тогда при помощи (1.20) уравнение (1.17) приводится к виду
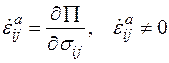 при
при  (1.21)
(1.21)
с суммированием по всем активным механизмам скольжения  . Полученные для монокристалла результаты могут служить основой при построении потенциальной функции для поликристаллического элементарного объема. В этом случае при помощи статистического усреднения определяется потенциальная функция
. Полученные для монокристалла результаты могут служить основой при построении потенциальной функции для поликристаллического элементарного объема. В этом случае при помощи статистического усреднения определяется потенциальная функция 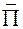 элементарного объема
элементарного объема  представляющего собой поликристаллический агрегат, и условие неупругого деформирования
представляющего собой поликристаллический агрегат, и условие неупругого деформирования 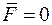 вводится следующим образом:
вводится следующим образом:
 (1.21)
(1.21)
где П и F — соответственно потенциальная функция и условие неупругого деформирования для монокристаллов, входящих в состав поликристаллического элементарного объема  , При помощи (1.22) получаем уравнение для
, При помощи (1.22) получаем уравнение для  вида (1.16). Функцию П можно выбрать в форме
вида (1.16). Функцию П можно выбрать в форме
 (1.23)
(1.23)
где

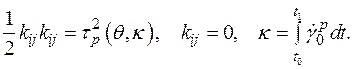 (1.24)
(1.24)
Можно также исходить из представления о микромеханизме вязкопластического течения как о комбинации двух эффектов: эффекта скольжения, при котором скольжение осуществляется после превышения приведенным касательным напряжением соответствующего предельного значения, и эффекта, связанного с тепловой активацией процесса вязкопластической деформации. Тепловая активация атомов способствует движению дислокаций, Существует определенный энергетический барьер, при превышении которого процесс активируется термически. Чем энергетическое состояние в рассматриваемой точке тела выше энергетического барьера, тем с большей скоростью будет протекать процесс вязкопластической деформации.
Мы предлагаем следующее обобщение одномерных результатов на трехмерный случай. За меру энергетического состояния в данной точке принимается удельная свободная энтальпия z, которая имеет определенное предельное значение 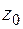 , описывающее в макромасштабе соответствующий энергетический барьер. Влияние разности
, описывающее в макромасштабе соответствующий энергетический барьер. Влияние разности 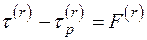 в макромасштабе описывается функцией F. При этих допущениях скорость неупругого деформирования имеет вид
в макромасштабе описывается функцией F. При этих допущениях скорость неупругого деформирования имеет вид
 при F>0 (11.25)
при F>0 (11.25)
где 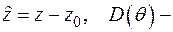 структурный коэффициент, зависящий от температуры
структурный коэффициент, зависящий от температуры 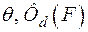 — характерная функция, которая в одномерных случаях определяется как степенная экспонента или гиперболический синус. Поскольку используется условие устойчивости Друккера для неупругих материалов, тензор
— характерная функция, которая в одномерных случаях определяется как степенная экспонента или гиперболический синус. Поскольку используется условие устойчивости Друккера для неупругих материалов, тензор  пропорционален градиенту
пропорционален градиенту 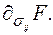 Второй множитель в (1.25) имеет экспоненциальный вид, так как считаем, что вероятность процесса активации определяется путем статистического усреднения из закона распределения Больцмана. Когда влияние величин
Второй множитель в (1.25) имеет экспоненциальный вид, так как считаем, что вероятность процесса активации определяется путем статистического усреднения из закона распределения Больцмана. Когда влияние величин  и
и 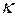 . на первые два множителя мало, можно. принять
. на первые два множителя мало, можно. принять
 при
при 
и получить определяющее уравнение (1.10). В других случаях, например для полимерных материалов с высокомолекулярной структурой, неупругая деформация связана не с механизмом скольжения, а главным образом с процессом термической активации и образования микротрещин. В этом случае можно положить 
Если статическое условие неупругого деформирования принято в виде (1.11) или (1.12). то

и скорость неупругой деформации  пропорциональна градиенту
пропорциональна градиенту  Для материалов, не обладающих пластическим упрочнением, когда
Для материалов, не обладающих пластическим упрочнением, когда  уравнение (1.10) можно записать в виде
уравнение (1.10) можно записать в виде
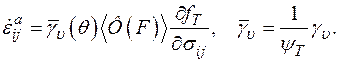 (1.26)
(1.26)
Применяя закон скорости неупругого течения вида (1.26) вместе с условиями (1.13), (1.14) или (1.15) при 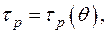 нужно учесть, что в первом случае
нужно учесть, что в первом случае
 во втором
во втором 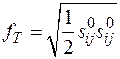 и в третьем
и в третьем  Тогда соответственно получим
Тогда соответственно получим
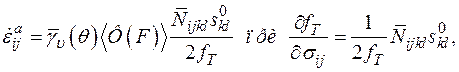 (1.27)
(1.27)
или
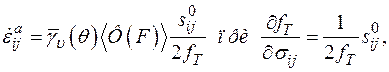 (1.28)
(1.28)
или
 (1.29)
(1.29)
Влияние температуры в формулах (1.27) — (1.28) отражено через изменение коэффициента вязкости  (растущего вместе с ростом температуры) и предела текучести
(растущего вместе с ростом температуры) и предела текучести  (вообще говоря, убывающего с ростом температуры). Конкретные выражения для функций
(вообще говоря, убывающего с ростом температуры). Конкретные выражения для функций  и
и 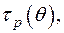 найденные экспериментально для некоторых материалов.
найденные экспериментально для некоторых материалов.
Если равенство (1.29) умножить тензорно само на себя, то для  получим
получим
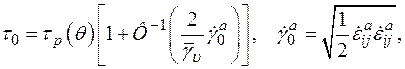 (1.30)
(1.30)
где  — функция, обратная функции Ф. Это уравнение можно интерпретировать как динамическое условие неупругого деформирования типа Мизеса
— функция, обратная функции Ф. Это уравнение можно интерпретировать как динамическое условие неупругого деформирования типа Мизеса 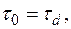 о Динамический предел неупругого деформирования
о Динамический предел неупругого деформирования
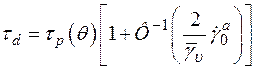
зависит от статического предела 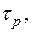 температуры
температуры  и скорости неупругой деформации
и скорости неупругой деформации 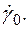 В данном случае влияние скорости деформации проявляется в виде своеобразного изотропного упрочнения материала.
В данном случае влияние скорости деформации проявляется в виде своеобразного изотропного упрочнения материала.
Некоторые авторы строят вязкопластические модели, исходя непосредственно из динамического условия неупругого деформирования с соответствующим ассоциированным законом течения. При этом делаются следующие предположения.
а) Обобщенные термодинамические силы и обобщенные термодина-мические потоки связаны, вообще говоря, нелинейными зависимостями, аналогичными зависимостям Онзагера в линейной необратимой термодина-мике. В данном случае это приводит к зависимости между  и
и 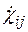 или, что одно и то же, между
или, что одно и то же, между 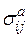 и
и 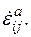 В частном случае можно использовать линейную зависимость
В частном случае можно использовать линейную зависимость
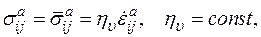 (1.31)
(1.31)
которая имеет вид уравнения Максвелла для линейно-вязко-упругих тел с коэффициентом вязкости 
б) Существует динамическое условие неупругого деформирования
 (1.32)
(1.32)
Часто считают, что влияние скорости неупругой деформации проявляется как внутренняя вязкость, описываемая, например. (1.31). В этом случае можно ввести активные напряжения по формуле
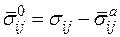 (1.33)
(1.33)
и принять, что 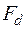 зависит от.
зависит от.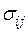 и
и  через
через 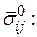
 (1.34)
(1.34)
Одним из часто применяемых динамических условий (1.34) служит условие типа условия Мизеса
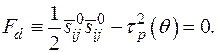 (1.35)
(1.35)
в) Материал неупруго несжимаемый, т.е.  и, следовательно,
и, следовательно,
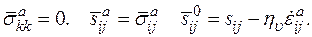 (1.36)
(1.36)
г) Скорость неупругой деформации  пропорциональна градиенту функции динамического неупругого деформирования
пропорциональна градиенту функции динамического неупругого деформирования 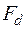 по отношению к напряжениям
по отношению к напряжениям 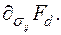
При этих предположениях и при допущениях, что неупругое деформирование зависит от активных напряжений (1.33), а динамическое условие неупругого деформирования имеет вид (1.34), для закона течения (такого же, как в теории упругопластических материалов) получаем следующие выражения:
 (1.37)
(1.37)
при
 если
если  и
и  (нагружение), (1.38)
(нагружение), (1.38)
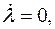 если
если  и
и  (разгрузка),
(разгрузка),
или  (область упругости).
(область упругости).
При этих допущениях вектор скорости неупругой деформации ортогонален актуальной поверхности динамического неупругого деформирования как в пространстве напряжений, так и в пространстве активных напряжений. К этому результату можно также прийти, если заменить предположение (г) постулатом Друккера об устойчивости неупругих материалов и вытекающими из него локальными неравенствами (1.8) и (1.9), но при условии, что допустимое напряжение 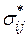 определяется как напряжение, для которого
определяется как напряжение, для которого 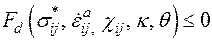 .
.
Если условие (1.35) ассоциировать с (1.37), то закон неупругого течения запишется в виде
 при
при 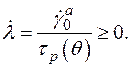 (1.39)
(1.39)
В случае изотермического процесса  в качестве динамического условия неупругого деформирования принято условие типа (1.30), имеющее вид
в качестве динамического условия неупругого деформирования принято условие типа (1.30), имеющее вид
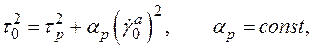 (1.40)
(1.40)
где  предел текучести при чистом сдвиге и статическом нагружении. Вообще говоря, он является функцией температуры
предел текучести при чистом сдвиге и статическом нагружении. Вообще говоря, он является функцией температуры  и параметра упрочнения
и параметра упрочнения 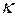 .
.
Рассматривая условие неупругого деформирования (1.40) совместно с законом неупругого течения вида (1.37), получаем
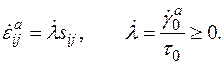 (1.41)
(1.41)
Предложенные выше определяющие уравнения для скорости неупругого деформирования без особых дополнительных видоизменений могут быть применены и к изотермическому случаю  Например, закон неупругого течения (1.29) принимает вид
Например, закон неупругого течения (1.29) принимает вид
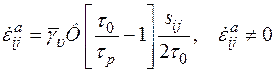 при
при  (1.42)
(1.42)
где 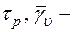 константы материала. Соответствующее этому закону динамическое условие будет иметь вид
константы материала. Соответствующее этому закону динамическое условие будет иметь вид
 (1.43)
(1.43)
Как видно из последнего выражения, если нагружение статическое и скорость неупругого деформирования мала, то корректирующим членом, содержащим 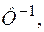 можно пренебречь; тогда получается условие текучести Мизеса
можно пренебречь; тогда получается условие текучести Мизеса 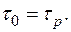 Переход к пластическому телу в написанном выше соотношении можно выполнить, устремляя
Переход к пластическому телу в написанном выше соотношении можно выполнить, устремляя  к бесконечности, т.е. полагая
к бесконечности, т.е. полагая 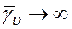 . Таким образом, вязкопластическое деформирование является более общим случаем, чем пластическое. Это обстоятельство можно объяснить также при помощи микромеханизма пластического и вязкопластического деформирования, который, например, у кристаллических материалов связан в обоих случаях с движением дислокаций и является прежде всего динамическим процессом.
. Таким образом, вязкопластическое деформирование является более общим случаем, чем пластическое. Это обстоятельство можно объяснить также при помощи микромеханизма пластического и вязкопластического деформирования, который, например, у кристаллических материалов связан в обоих случаях с движением дислокаций и является прежде всего динамическим процессом.
Чтобы получить полную систему определяющих уравнений для рассматриваемого типа тел, необходимо к выражению для  добавить выражения для
добавить выражения для 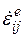 и
и  зависящие от выбора
зависящие от выбора 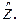 При подходящем выборе функции удельной свободной энтальпии можно получить различные частные случаи упругого и термического поведения тел, а также соответствующие уравнения теплопроводности и неравенства второго закона термодинамики. В качестве иллюстрации приведем эти уравнения для случая, когда они описывают линейно-упругие и термические свойства тела и вязкопластические свойства без пластического упрочнения, заданные законом неупругого деформирования (1.29). В этом случае функцию
При подходящем выборе функции удельной свободной энтальпии можно получить различные частные случаи упругого и термического поведения тел, а также соответствующие уравнения теплопроводности и неравенства второго закона термодинамики. В качестве иллюстрации приведем эти уравнения для случая, когда они описывают линейно-упругие и термические свойства тела и вязкопластические свойства без пластического упрочнения, заданные законом неупругого деформирования (1.29). В этом случае функцию 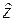 выбираем в виде
выбираем в виде
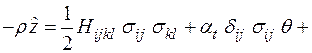 (1.44)
(1.44)
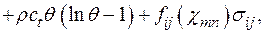
где  — тензор четвертого ранга с постоянными коэффициентами, обладающий симметрией
— тензор четвертого ранга с постоянными коэффициентами, обладающий симметрией 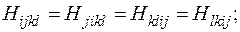
 и
и 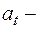 термические постоянные материала. Уравнение для скорости деформации принимает вид
термические постоянные материала. Уравнение для скорости деформации принимает вид
 (1.45)
(1.45)
а уравнение эволюции для 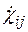 — вид
— вид
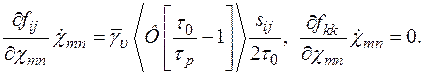 (1.46)
(1.46)
Уравнение для температуры принимает форму
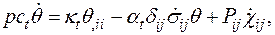 (1.47)
(1.47)
где
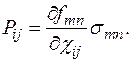 (1.48)
(1.48)
Учитывая (1.46) и (1.48), уравнение (1.47) можно представить в виде
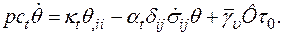 (1.49)
(1.49)
Неравенство второго принципа термодинамики дает
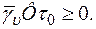 (1.50)
(1.50)
Таким образом, функция Ф должна быть неотрицательной, так как по определению  а по предположению
а по предположению 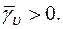 В изотермическом случае
В изотермическом случае  уравнение (1.45) запишется в виде
уравнение (1.45) запишется в виде
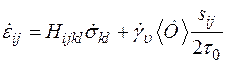 при
при 
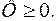 (1.51)
(1.51)
При простом нагружении можно дополнительно линеаризовать уравнение для 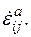 При
При 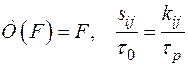 , и '
, и '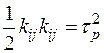 уравнение для скорости неупругой деформации принимает вид
уравнение для скорости неупругой деформации принимает вид
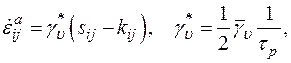 (1.52)
(1.52)
 при
при 
В частных задачах, когда распределение 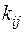 известно, уравнение (1.52) дает линейную связь между
известно, уравнение (1.52) дает линейную связь между  и
и 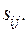 Эта линеаризация облегчает решение конкретных вязкопластических задач и применяется даже при малых отклонениях от простого нагружения. В приложениях часто используется линеаризованная вязкопластическая модель Прагера, представляющая собой своеобразное применение понятия вязкопластического деформирования к кусочно-линейному условию неупругого деформирования типа Треска. Согласно этой модели, закон неупругого течения имеет вид
Эта линеаризация облегчает решение конкретных вязкопластических задач и применяется даже при малых отклонениях от простого нагружения. В приложениях часто используется линеаризованная вязкопластическая модель Прагера, представляющая собой своеобразное применение понятия вязкопластического деформирования к кусочно-линейному условию неупругого деформирования типа Треска. Согласно этой модели, закон неупругого течения имеет вид
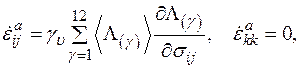 (1.53)
(1.53)
где
 при
при 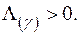 (1.54)
(1.54)
 при
при 
В пространстве главных напряжений  описывает плоскости, заданные уравнениями
описывает плоскости, заданные уравнениями

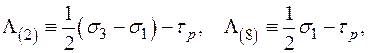
 (1.55)
(1.55)

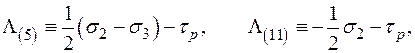
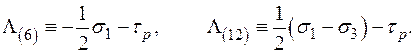
Если считать, что  и
и  являются функциями
являются функциями  , то получим линеаризованные определяющие уравнения рассматриваемого типа для термовязкопластических тел.
, то получим линеаризованные определяющие уравнения рассматриваемого типа для термовязкопластических тел.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 575; Нарушение авторских прав?; Мы поможем в написании вашей работы!