Предельные точки последовательности

Определение 1. Точка x бесконечной прямой называется предельной точкой последовательности {x_n}, если в любой e - окрестности этой точки имеется бесконечно много элементов последовательности {x_n}.

Лемма 1. Если x- предельная точка последовательности {x_k}, то из этой последовательности можно выделить подпоследовательность {x_nk}, сходящуюся к числу x.

Замечание. Справедливо и обратное утверждение. Если из последовательности {x_k} можно выделить подпоследовательность, сходящуюся к числу x, то число x является предельной точкой последовательности {x_k}. Действительно, в любой e - окрестности точки x имеется бесконечно много элементов подпоследовательности, а стало быть и самой последовательности {x_k}.

Из леммы 1 следует, что можно дать другое определение предельной точки последовательности, эквивалентное определению 1.

Определение 2. Точка x бесконечно прямой называется предельной точкой последовательности {x_k}, если из этой последовательности можно выделить подпоследовательность, сходящуюся к x.

Лемма 2. Каждая сходящаяся последовательность имеет только одну предельную точку, совпадающую с пределом этой последовательности.

Замечание. Если последовательность сходится, то она в силу леммы 2 имеет только одну предельную точку. Однако, если {x_n} не является сходящейся, то она может иметь несколько предельных точек (и, вообще бесконечно много предельных точек). Покажем, например, что {1+(-1)ⁿ} имеет две предельные точки.

Действительно, {1+(-1)ⁿ}=0,2,0,2,0,2,... имеет две предельные точки 0 и 2, т.к. подпоследовательности {0}=0,0,0,... и {2}=2,2,2,... этой последовательности имеют пределами соответственно числа 0 и 2. Других предельных точек у этой последовательности нет. Действительно, пусть x -любая точка числовой оси, отличная от точек 0 и 2. Возьмем e >0 настолько

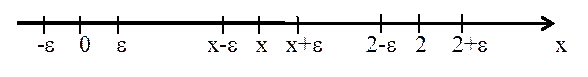
малым, чтобы e - окрестности точек 0, x и 2 не пересекались. В e- окрестностях точек 0 и 2 содержатся все элементы последовательности и поэтому e - окрестность точки x не может содержать бесконечно много элементов {1+(-1)ⁿ} и поэтому не является предельной точкой этой последовательности.

Теорема. У всякой ограниченной последовательности существует хотя бы одна предельная точка.

Замечание. Ни одно число x, превосходящее 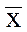, не является предельной точкой последовательности {x_n}, т.е. 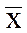- наибольшая предельная точка последовательности {x_n}.

Пусть x- любое число, превосходящее 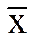. Выберем e>0 настолько малым,

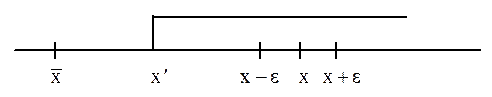
что x-e>.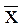

Так как

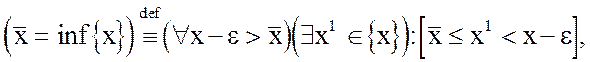
и x¹ Î{x}, правее x¹ лежит конечное число элементов последовательности {x_n} или их вовсе нет, т.е. x не является предельной точкой последовательности {x_n}.

Определение. Наибольшая предельная точка 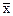последовательности {x_n} называется верхним пределом последовательности и обозначается символом 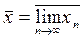. Из замечания следует, что у всякой ограниченной последовательности есть верхний предел.

Аналогично вводится понятие нижнего предела 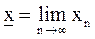(как наименьшей предельной точки последовательности {x_n}).

Итак, мы доказали следующее утверждение. У всякой ограниченной последовательности существует верхний и нижний пределы.

Сформулируем без доказательства следующую теорему.

Теорема. Для того, чтобы последовательность {x_n} была сходящейся, необходимо и достаточно, чтобы она была ограниченной и чтобы ее верхний и нижний пределы 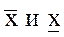совпадали.

Результаты этого пункта приводят к следующей основной теореме Больцано-Вейерштрасса.

Теорема Больцано-Вейерштрасса. Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.

Доказательство. Так как последовательность {x_n} ограничена, то она имеет хотя бы одну предельную точку x. Тогда из этой последовательности можно выделить подпоследовательность, сходящуюся к точке x (следует из определения 2 предельной точки).

Замечание. Из любой ограниченной последовательности можно выделить монотонную сходящуюся последовательность.

Дата добавления: 2014-01-07