Пример построения интервального вариационного ряда

Пусть измерен некоторый экономический показатель в 30 регионах:

23 29 35 7 11 18 23 30 36 18 11 8 13 20 25 27 14 30 20 20 24 19 21 26 22 16 26 25 33 27

Расставим экспериментальные данные в возрастающем порядке:

6 8 11 11 13 14 16 18 18 19 20 20 20 21 22 23 23 24 25 25 26 26 27 27 29 30 30 33 35 36

По таблице 1 определяем число классов

Таблица 1

Объем выборки n	Число классов K
6-11
12-22
23-46
47-93
94-187
188-377
378-755
756-1515

Для n=30 число классов K=6. Найдем минимальное и максимальное значения вариант: х_min=7, х_max=36. Определим вариационный размах R= х_min-х_max=36-6=30.

Определим величину классового интервала: D=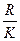==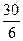5.

Х_н1= х_min=6; Х_в1= х_min+D=6+5=11

Обобщим полученные данные в таблице:

Таблица 2

Номера классов	Классовые интервалы	Серединные значения классов	Частоты	Накопленные частоты
	6-11	8,5
	11-16	13,5
	16-21	18,5
	21-26	23,5
	26-31	28,5
	31-36	33,5

График, называемый гистограммой получается, если в прямоугольной системе координат отложить по оси абсцисс границы классов, а по оси ординат их частоты.

Если серединные точки вершин прямоугольников гистограммы соединить между собой, получится график дискретного варьирования, называемый полигоном распределения.

1.2. Мода распределения – это наиболее часто встречающееся значение ряда.

1.3. Среднее арифметическое распределения находится по формуле
х_ср= (х₁+х₂+х₃+ …+х_n)/n

1.4. Дисперсия распределения находится по формуле:

D=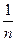

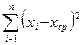
1.5. Стандартное отклонение S=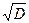

Дата добавления: 2014-01-07