
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Площадь поверхности вращения
Пусть кривая 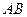 задана уравнением
задана уравнением 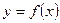 ,
, 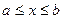 , и пусть функция
, и пусть функция 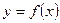
 неотрицательна и непрерывна вместе со своей первой производной на
неотрицательна и непрерывна вместе со своей первой производной на 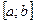 . Тогда поверхность, образованная вращением кривой
. Тогда поверхность, образованная вращением кривой 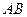 вокруг оси
вокруг оси 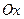 (Рис.19.7.), имеет площадь
(Рис.19.7.), имеет площадь 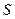 , которая может быть вычислена по формуле
, которая может быть вычислена по формуле
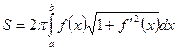 .
.
Если же поверхность получается вращением кривой 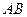 , заданной уравнением
, заданной уравнением 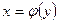 ,
, 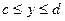 , вокруг оси
, вокруг оси 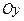 , то площадь такой поверхности вычисляется по формуле
, то площадь такой поверхности вычисляется по формуле
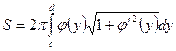 .
.
 Пример. Часть сферы, вырезаемая двумя параллельными плоскостями, находящимися на расстоянии
Пример. Часть сферы, вырезаемая двумя параллельными плоскостями, находящимися на расстоянии  друг от друга, называется шаровым поясом высоты
друг от друга, называется шаровым поясом высоты  . Вычислить площадь шарового пояса высоты
. Вычислить площадь шарового пояса высоты  , если радиус шара равен
, если радиус шара равен 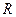 (Рис.19.8.).
(Рис.19.8.).
Решение. Поверхность шарового пояса можно рассматривать как поверхность,
полученную при вращении дуги окружности
 , где
, где 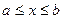 ,
, 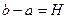 , вокруг оси
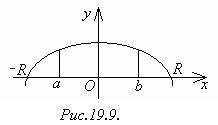
, вокруг оси 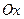 (Рис.19.9.). Так как
(Рис.19.9.). Так как 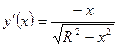 , то
, то
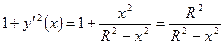 .
.
Тогда  =
=  =
= 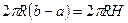 .
.
В частности, если 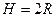 , то получаем площадь поверхности сферы
, то получаем площадь поверхности сферы 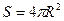 .
.
19.7.4. Объём тела.
Рассмотрим некоторое тело и вычислим его объём 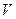 . Допустим, что известны площади сечений этого тела плоскостями, перпендикулярными оси
. Допустим, что известны площади сечений этого тела плоскостями, перпендикулярными оси 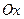 . С изменением
. С изменением  меняется и площадь сечения, т.е. площадь сечения является некоторой функцией
меняется и площадь сечения, т.е. площадь сечения является некоторой функцией 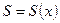 . Если эта функция непрерывна на
. Если эта функция непрерывна на 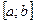 , то объём тела
, то объём тела

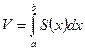 .
.
В частности, если тело образовано вращением вокруг оси 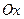 криволинейной трапеции, ограниченной сверху дугой
криволинейной трапеции, ограниченной сверху дугой 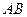 непрерывной линии
непрерывной линии 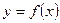 , где
, где 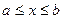 (Рис.19.10.), то
(Рис.19.10.), то 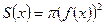 и получаем формулу
и получаем формулу
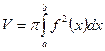 .
.
Если же тело получено вращением вокруг оси 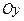 криволинейной трапеции, ограниченной дугой
криволинейной трапеции, ограниченной дугой 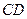 линии
линии 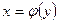 ,
, 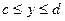 , то его объём
, то его объём
 .
.
Пример. Вычислить объём тела, полученного вращением вокруг оси 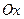 криволинейной трапеции, ограниченной линиями
криволинейной трапеции, ограниченной линиями 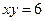 ,
, 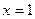 ,
, 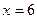 (Рис.19.11.).
(Рис.19.11.).
 Решение.
Решение. 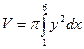 =
= 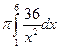 =
= 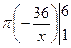 =
= 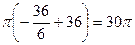 .
.
|
Дата добавления: 2014-01-07; Просмотров: 428; Нарушение авторских прав?; Мы поможем в написании вашей работы!