Casep^.iBalance of

Begin

Else

End

Begin

Begin

Var

Else

Begin

Else

End

Begin

Else

End

Begin

Else

End

Begin

Else

Else

Begin

Var

Begin

Begin

End.

Begin

Begin

Begin

Var

Begin

New(PCurr);

Readln(F, pCurr^.iKey);

pCurr^.pLeft:= Nil;

pCurr^.pRight:= Nil;

Inc(nItem);

SetLength(mItem, nItem);

mItem[nItem - 1]:= pCurr;

end;

CloseFile(F);

end;

procedure MakeTree(var pFrom: pMyNodeType; iFrom, iTo: integer);

i: integer;

if iFrom > iTo then Exit;

i:= (iFrom + iTo) div 2;

pFrom:= mItem[i];

MakeTree(pFrom^.pLeft, iFrom, i - 1);

MakeTree(pFrom^.pRight, i + 1, iTo);

end;

procedure Detour(pStart: pMyNodeType; Level: integer);

var i: integer;

for i:=1 to Level do Write(Chr(32));

WriteLN(pStart^.iKey);

Detour(pStart^.pLeft, Level + 1);

Detour(pStart^.pRight, Level + 1);

end;

pRoot:= Nil;

ReadItems;

MakeTree(pRoot, 0, nItem-1);

Detour(pRoot, 0).

if pFrom = nil then

New(pFrom);

pFrom^.iKey:= iKey;

pFrom^.pLeft:= nil;

pFrom^.pRight:= nil;

Exit;

end;

if iKey = pFrom^.iKey then Halt;

if iKey < pFrom^.iKey then

IncludeKey(pFrom^.pLeft, iKey)

else // iKey > pFrom^.iKey

IncludeKey(pFrom^.pRight, iKey)

end;

Исключение из двоичного дерева поиска

Для удаления существующего ключа применяется рекурсивно вызываемая процедура ExcludeKey. Она проникает вглубь дерева поиска, пытаясь отыскать в дереве предлагаемый к удалению ключ. Если дерево пусто, приложение аварийно завершается.

При проникновении в дерево отношение «больше – меньше» используется для поиска того места, где удаляемый ключ должен быть, если дерево является деревом поиска. Если та ссылка, по которой далее следует искать место для iKey, указывает в «никуда» (pFrom = nil), приложение аварийно завершается.

Если ключ (узел pFrom), который нужно удалить, найден, рассматривается четыре возможных ситуации с его потомками.

1. Обоих потомков нет. Ссылку от узла-предка обнуляем, а сам удаляемый узел выбрасываем из памяти.

2. Есть только левый потомок. Ссылку от узла-предка перенацеливаем на этого левого потомка, а сам удаляемый узел выбрасываем из памяти.

3. Есть только правый потомок. Ссылку от узла-предка перенацеливаем на этого правого потомка, а сам удаляемый узел выбрасываем из памяти.

4. Есть оба потомка. Углубляемся в левое поддерево, разыскиваем в нем самый правый из левых потомков (СПЛП). Когда поиск завершается, обмениваем значениями ключи в СПЛП и pFrom. Возникает случай 2.

procedure ExcludeKey(var pFrom: pMyNodeType; iKey: integer);

pCurr, pPrev: pMyNodeType;

if pFrom = nil then Halt;

if iKey < pFrom^.iKey then

ExcludeKey(pFrom^.pLeft, iKey)

if iKey > pFrom^.iKey then

ExcludeKey(pFrom^.pRight, iKey)

// Сюда попали => мы на том самом узле и ключе, который нужно удалить

begin // Удаляем именно этот узел

if (pFrom^.pLeft = nil) and (pFrom^.pRight = nil) then

Dispose(pFrom);

pFrom:= nil;

if pFrom^.pLeft = nil then // Есть только правое поддерево

pCurr:= pFrom^.pRight; // <> nil

Dispose(pFrom);

pFrom:= pCurr;

if pFrom^.pRight = nil then // Есть только левое поддерево

pCurr:= pFrom^.pLeft; // <> nil

Dispose(pFrom);

pFrom:= pCurr;

begin // Есть ОБА поддерева

pCurr:= pFrom^.pLeft; // <> nil

pPrev:= nil;

while pCurr^.pRight <> nil do

pPrev:= pCurr;

pCurr:= pCurr^.pRight;

end;

pFrom^.iKey:= pCurr^.iKey;

if pPrev = nil then

pFrom^.pLeft:= pCurr^.pLeft

pPrev^.pRight:= pCurr^.pLeft;

Dispose(pCurr);

end; // Есть ОБА поддерева

end; // Удаляем именно этот узел

end;

Графическое представление деревьев

На данном этапе графическое представление будет использовано только для деревьев поиска.

Графическое представление дерева может быть организовано несколькими способами. Первый, самый простой, показан на Рисунке 1.

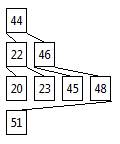
Рис.1

Узлы для каждого значения глубины (глубины 0 для узла «44», глубины 1 для узлов «22», «46», и т.д.) располагаются, начиная с меньшего ключа, прижатого к левому краю рисунка, и далее в порядке роста ключей на данной глубине. Если через узлы провести вертикальные линии, на самой левой вертикали будет Располагаться больше всего узлов, на второй вертикали – меньше, на третьей, возможно, еще меньше (во всяком случае, не больше), и т.д.

Этот способ представления, кроме простоты, других достоинств не имеет.

Недостатки:

1. Дерево выглядит некрасиво. Чем больше глубина (высота) дерева, тем более вытянутыми становятся линии связи от предка к потомку.

2. Левые потомки узла могут оказаться «правее» этого узла. Как, например, левый потомок «45» узла «46».

3. Правые потомки узла могут оказаться «левее» этого узла. Как, например, правый потомок «51» узла «48».

Таким образом, это графическое представление не вполне согласуется с принципами дерева поиска «Всё, что левее – меньше, всё, что правее – больше».

На Рисунке 2 такой принцип уже полностью соблюден. И выглядит дерево вполне пристойно. Оно, можно сказать, похоже на настоящее дерево. Конечно, линии связи между «неглубокими» (близкими к корню) узлами длинноваты, но это неизбежно. Зеленым цветом показан узел, возникший последним.

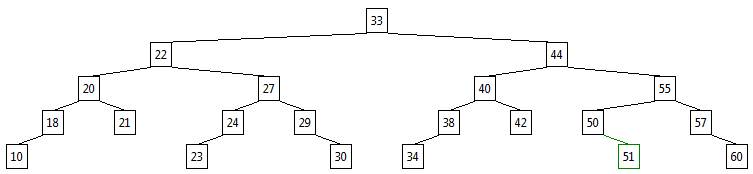
Рис.2

Для ключей такого дерева справедливо утверждение: все узлы, расположенные справа от данного узла, имеют ключи, большие, чем на данном узле, а все узлы, расположенные слева от данного узла, имеют ключи, меньшие, чем на данном узле. Причем, это относится не только к узлам-потомкам данного узла, но и ко всем остальным узлам. Следовательно, можно утверждать: каждый узел занимает свою «индивидуальную» вертикаль, второго узла на этой же вертикали нет. При любой перестройке дерева с данным набором ключей каждый из узлов может перейти на другую глубину, сменить потомков и/или предков, но вертикаль свою не покинет.

Теперь пора обсудить, как такое дерево изобразить.

Каждый прямоугольник, изображающий узел, характеризуется координатами верхнего левого угла (полями X и Y). Ширина прямоугольника представлена полем iBoxWidth, она для каждого ключа своя (символы в ключе имеют каждый свою ширину, да и количества символов в ключе могут быть разными). Y-координата может управляться глубиной узла, которая является одним из параметров функции Detour («Обход»). X-координата должна зависеть от порядкового номера «индивидуальной» вертикали, а значит, от порядкового номера ключа. Это означает, что ключи перед их прорисовкой на экране должны быть отсортированы в порядке возрастания. Это делается с помощью организации второй, «параллельной» структуры данных (из тех же ключей) в виде линейного однонаправленного отсортированного списка. Постановка каждого нового ключа в сортированный список рассматривалась на предыдущих лекциях, поэтому об организации линейного списка здесь будет сказано кратко.

Итак, для доступа к основной структуре «Дерево» требуется глобальная переменная pRoot – указатель на корневой узел дерева. Связными для дерева являются поля pLeft и pRight.

Для доступа к параллельной структуре «Линейный список» требуется глобальная переменная pHead – указатель на узел с меньшим ключом. Связным для списка является поле pNext.

Конечно, атрибуты параллельной структуры «отягощают» дерево. Но следует помнить, что они вводятся здесь только для визуализации дерева в рамках учебного процесса. Визуализировать дерево в промышленных масштабах вряд ли придется.

Включение в сбалансированное дерево

pMyNodeType = ^MyKnot;

MyKnot = record

iKey: longint;

pLeft, pRight: pMyNodeType;

iBalance: integer;

end;

// iBalance = <Высота правого поддерева> – < Высота левого поддерева >

Пусть h_L – высота левого поддерева, h_R – высота правого поддерева.

Возможны следующие ситуации при включении очередного узла в сбалансированное дерево.

0. Новый узел не изменил высоту ни левого, ни правого поддерева. Баланс не нарушен.

1. Новый узел был включен в левое поддерево и увеличил его высоту на единицу.

1(а). До включения было h_L < h_R (т.е. h_L = h_R – 1), => после включения стало h_L = h_R, баланс даже улучшился.

1(б). До включения было h_L = h_R, => после включения стало h_L = h_R + 1, баланс не нарушился (дерево не перестало быть сбалансированным).

1(в). До включения было h_L > h_R (т.е. h_L = h_R + 1), => после включения стало h_L = h_R + 2, требуется восстановление баланса. Способы восстановления показаны на Рис. 1 и Рис. 2.

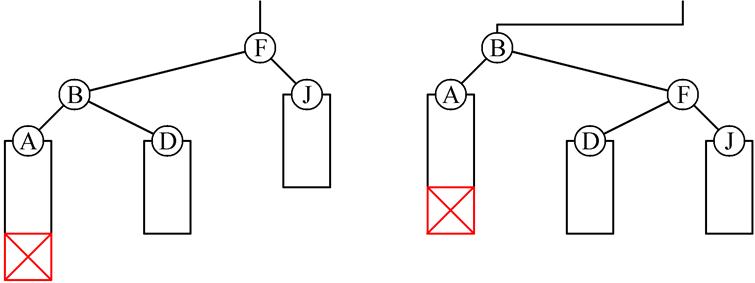
Было Стало

Рис.1

Было Стало

Рис.2

2. Новый узел был включен в правое поддерево и увеличил его высоту на единицу.

2(а). До включения было h_L > h_R (т.е. h_L = h_R + 1), => после включения стало h_L = h_R, баланс даже улучшился.

2(б). До включения было h_L = h_R, => после включения стало h_L = h_R - 1, баланс не нарушился (дерево не перестало быть сбалансированным).

2(в). До включения было h_L < h_R (т.е. h_L = h_R – 1), => после включения стало h_L = h_R – 2, требуется восстановление баланса. Способы восстановления показаны на Рис. 3 и Рис. 4.

Было Стало

Рис.3

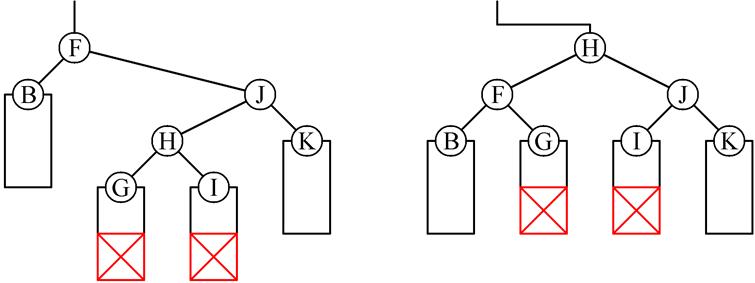
Было Стало

Рис.4

procedure IncludeKey(var p: pMyNodeType; iKey: integer; var bBecameHigher: boolean);

p1, p2: pMyNodeType;

if p = nil then

New(p);

bBecameHigher:= true; // Tree became higher

p^.iKey:= iKey;

p^.pLeft:= nil;

p^.pRight:= nil;

p^.iBalance:= 0;

if iKey < p^.iKey then

IncludeKey(iKey, p^.pLeft, bBecameHigher);

if bBecameHigher then // Left branch became higher

+1:

Дата добавления: 2014-01-07