Линейный гармонический осциллятор

в квантовой механике.

Линейный гармонический осциллятор – это система, совершающая одномерное движение под действием квазиупругой силы. Он является моделью, используемой во многих задачах классической и квантовой теории. Пружинный, физический и математический маятники – примеры классических гармонических осцилляторов. Потенциальная энергия гармонического осциллятора равна: 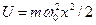, (5.1)

где 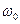— собственная частота колебаний осциллятора, т — масса частицы.

Рассмотрим сначала поведение классического гармонического осциллятора. Пусть частица с полной энергией совершает колебания в силовом поле (4.77) (рис.4.24). Точк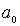и и 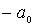, в которых полная энергия частицы равна потенциальной энергии , являются для частицы точками поворота. Частица совершает колебательные движения между стенками потенциальной ямы внутри отрезка 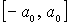, выйти за пределы которого она не может. Амплитуда колебаний 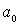определяется выражением .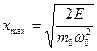

Зависимость (5.1) имеет вид параболы (рис. 5.1), т.е. «потенциальная яма» в данном случае является параболической. Амплитуда малых колебаний классического осциллятора определяется его полной энергией Е. В точках с координатами ±х_max полная энергия Е равна потенциальной энергии. Поэтому с классической точки зрения частица не может выйти за пределы области (– х_max, + х_max).

Гармонический осциллятор в квантовой механике – квантовый осциллятор – опи­сывается уравнением Шредингера (4.2), учитывающим выражение (5.1) для потенциальной энергии. Тогда стационарные состояния квантового осциллятора определяются уравнением Шредингера вида

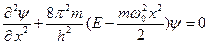(5.2)

где Е — полная энергия осциллятора. В теории дифференциальных уравнений до­казывается, что уравнение (5.2) решается только при собственных значениях энергии

(5.3)

где . Формула (5.3) показывает, что энергия квантового осциллятора может иметь лишь дискретные значения, т.е. квантуется.

Это соотношение и определяет закон квантования энергии гармонического осциллятора. Отметим, что энергетические уровни гармонического осциллятора, в отличие, например, от случая прямоугольной потенциальной ямы, являются эквидистантными, т.е. расположены на одинаковом энергетическом расстоянии друг от друга

Энергия ограничена снизу отличным от нуля минималь­ным значением энергии 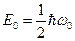. Существование минимальной энергии, назы­ваемой энергией нулевых колебаний, пред­ставляет собой прямое следствие соотношения неопределенностей.

Поместим начало координат в точку, являющуюся положением равновесия гармонического осциллятора, совершающего колебания по закону . Тогда неопределенность координаты принимает вид

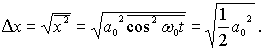
Амплитуда колебаний 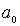связана с энергией 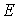соотношением , следовательно

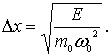
Аналогично, для неопределенности импульса имеем

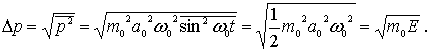
Подставляя и 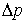в соотношение неопределенностей , получаем следующее условие

т.е. действительно, минимальное значение энергии гармонического осциллятора есть .

Нулевые колебания играют в физике весьма важную роль, в частности они обусловливают отсутствие кристаллизации жидкого гелия при нормальном давлении даже при абсолютном нуле температур. Велика роль нулевых колебаний и в объяснении природы сил молекулярных взаимодействий, физических особенностей поверхностного натяжения, адсорбции и других молекулярных явлений. На эксперименте наличие нулевых колебаний наблюдается, в частности, в опытах по рассеянию света кристаллами при низких температурах.

Наличие нулевых колебаний означает, что частица не может находиться на дне «потенциальной ямы», причем этот вывод не зависит от ее формы. В самом деле, «падение на дно ямы» связано с обращением в нуль импульса частицы, а вместе с тем и его неопределенности. Тогда неопределенность координаты становится сколь угодно большой, что противоречит, в свою очередь, пребыванию частицы в «потенциальной яме».

Вывод о наличии энергии нулевых колебаний квантового осциллятора противоре­чит выводам классической теории. Например, классическая физика приводит к выводу, что при Т=0 К (Е_к=0) энергия колебательного движения атомов кристалла должна обращаться в нуль. Однако эксперименты по рассеянию света показывают, что при Т®0 колебания атомов в кристалле не прекращаются.

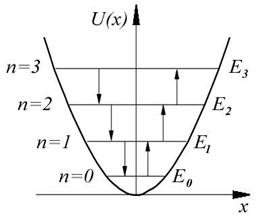
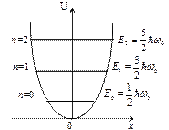
Из формулы (5.3) также следует, что уровни энергии линейного гармонического осциллятора расположены на одинаковых расстояниях друг от друга (рис. 5.2), а имен­но расстояние между соседними энергетическими уровнями равно , причем мини­мальное значение энергии ½.

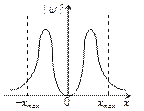Квантово-механический расчет показывает, что частицу можно обнаружить за пределами дозволенной области (– х_max, + х_max), в то время как с классической точки зрения она не может выйти за ее пределы. Следовательно, имеется отличная от нуля вероят­ность обнаружить частицу в той области, которая является классически запрещенной. Этот результат (без вывода) демонстрируется на рис.5.3, где приводится квантовая плотность вероятности 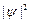обнаружения осциллятора для состояния п =1. Из рисунка следует, что для квантового осциллятора действительно плотность вероятности имеет конечные значения за пределами классически дозволенной области |x|³ х_max, т.е. имеется конечная (но небольшая) вероятность обнаружить частицу за пределами «потенциальной ямы».

Приведем вид волновых функций для первых трех энергетических уровней гармонического осциллятора

(4.85)

Графики волновых функций для значений квантового числа от 0 до 5 представлены на рис.4.26. Отрезок 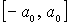определяет область, в

Рис. 4.26.

которой совершал бы колебания классический осциллятор. Ширина этой области оказывается различной для разных значений квантового числа , поскольку энергия осциллятора, а, следовательно, и амплитуда его колебаний также зависят от .

Дата добавления: 2014-01-07