Представления технологических процессов и систем

Классификация технологических процессов и систем

РАЗРАБОТКА СТРУКТУРЫ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ФУНКЦИОНИРОВАНИЯ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ ОМД

Проблемы, встающие при построении математических моделей, связаны с построением множества Z (1.2), отображений g (1.5), y (1.6) и выходного отображения j (1.7) и изучением их свойств. Это круг проблем анализа систем. Анализ обычно начинают с выявления всех факторов, которые оказывают влияние на поведение изучаемой системы. По существу, эта проблема связана с изучением и описанием множеств U, U (×), Y и Y (×). Далее встает задача описания динамических взаимосвязей между входами и выходами, т. е. задача построения модели этих связей, которая называется проблемой идентификации. С проблемой идентификации тесно связана проблема представления системы, где должны быть изучены возможные описания закономерностей поведения, т. е. возможная форма отображений g, y и j. С точки зрения синтеза эта проблема состоит в построении системы, реализующей заданное вход – выход поведение.

Классификация необходима для установления математического строения описывающих ТП множеств и отображений.

ТП называется дискретным, если U ={ u_k: k =0, 1,..., K }, причём T ={ t_k: k =0, 1,..., K } при условии t_k-1 < t_k и u_k (t_k). Для систем этого класса характерно Q ={ q (t_k) = g(t_k; u_k (t_k))} и Z ={ z (t_k +t)=y(t_k + t; t_k, q (t_k))}.

ТП называется непрерывным, если U ={ u (t): t Î [0, T ]}, T не аддитивно, а непрерывно, тогда Q ={ q (t) = g(t; t₀, u (t₀)} и Z = { z (t) = y(t; t₀, t, q(t, ×)}.

ТП называется стационарным, если 1) T является аддитивной группой; 2) для любого tÎ T из q(×) Î Q (×) следует (×) Î U(×), где для всех tÎ T выполняется равенство (t – t) = u(t); 3) y(t; t ₀, q(×)) = y(t – t; t ₀ – t, (×)) для всех tÎ T;

4) отображение j(t; t, z (×)) не зависит от t.

ТП называется нестационарным, если не выполнены условия стационарности.

ТП называется ограниченным первоначальной настройкой, если V = Æ,и полуограниченным, если в процессе функционирования отсутствует возможность управления размерами и формой области пластической деформации (например, процессы волочения, прессования, объемной штамповки и т.п.).

ТП называется (вполне) управляемым, если из любого состояния в данный момент времени его можно перевести в любое другое состояние под действием некоторого управления, т. е.

y (z', v) = z ''

и разрешимо относительно v при любых z ' и z''.

ТП называется наблюдаемым, если с формальной стороны восстановление начального состояния z по известным v и y сводится к решению уравнения y =j(z, v) относительно неизвестного z.

ТП называется настраиваемым (задача установочности), если при помощи фиксированного управления его можно перевести в фиксированное конечное состояние независимо от начального, т. е.

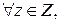y (z, v ^*) = z ^*,

состояние z ^* называется установочным, а управление v ^* – установочным управлением.

Важной проблемой анализа ТП является проблема устойчивости. Она возникает при изучении вопроса, будет ли ТП выполнять свою функцию и назначение в условиях, когда возникают различные возмущения, что часто является проявлением неполного знания об окружающей среде и самом процессе. Пусть назначение ТП состоит в преобразовании входа u ⁰(×), который опосредованно через q (×) порождает процесс z ⁰(×), в выход u ^к(×)≡ y ⁰(·). Если в результате каких–то обстоятельств процесс z (×) в пространстве состояний не совпадает с z ⁰(×), т. е. z ^*(t ₀) = z ⁰(t ₀) + D z (t ₀), что может быть следствием того, что в момент t ₀ появилось отклонение D z (t ₀), то естественно возникает вопрос, сходится ли при t > t ₀ и t ®¥ процесс y ^*(t) = j(x ⁰, t, z ^* (t)) в некотором смысле к процессу y ⁰(·) или будет близким к нему. Указанная сходимость будет иметь место, если j(x ⁰, t, t ₀, z ⁰ + D z, u ⁰(·)) будет сходиться к j(x ⁰, t, t ₀, z⁰, u ⁰(·)). Процесс z ⁰(t) называется невозмущенным движением, а процесс z ^* (×) – возмущенным движением. Изучение свойств отображения j, которые обеспечивают указанную сходимость процессов или их близость, составляет предмет теории устойчивости систем.

Исходными данными при постановке задач исследования технологических процессов являются только входы и выходы, т.е. их внешнее описание. Для установления структуры представления отображений, описывающих закономерности изменения состояний, необходимо рассмотреть разрешимость нахождения этих закономерностей по наблюдаемым входам и выходам. Рассмотрение будем выполнять с двух позиций:

1) формирования конечного состояния обработанного продукта, идентифицируемого характеристиками качества;

2) выхода ТП как результата функционирования по критериям точности, стабильности и надёжности.

При реализации процесса моделирования необходимо создавать модели для конкретных технологических процессов, как сложных систем. При решении этого вопроса сложную систему необходимо разбить на такую совокупность подсистем, которая наилучшим образом отражала бы работу и функциональное взаимодействие всех ее элементов. Использование такого принципа декомпозиции системы на подсистемы, подсистем на элементы позволяет создать модель сложной системы, опираясь на моделирующие алгоритмы элементов и алгоритмы их функционального взаимодействия. Совокупность моделирующих алгоритмов для элементов, разработанных указанным способом, с учетом алгоритма их взаимодействия определит исходный моделирующий алгоритм системы.

При создании моделей сложных систем практически всегда возникает вопрос о необходимости перехода к более сложным (или более простым) описаниям некоторых реальных элементов. В этом направлении широко известны работы И. Н. Коваленко [19] по кусочно–линейным агрегатам и описанию структуры систем многоуровневых схем сопряжения.

Элементами модели (1.4) являются отображения g (1.5) и y (1.6), поэтому рассмотрим некоторые обобщения, которые можно применить к этим отображениям. Множество Q значений основной распределенной/сосредоточенной технологической нагрузки q (×), g: T ´ U ® Q включает значения сил, нормальных и касательных напряжений, а также температур, распределенных на границе контакта между деформируемым металлом и инструментом.

Для обработки металлов давлением характерны две следующие группы процессов, которые связаны с условиями приложения основной распределенной/сосредоточенной технологической нагрузки q (×) [20]. Группы разделим по характеру передачи силового воздействие на область пластической деформации:

Непосредственно поверхностью инструмента – процессы прокатки, ковки и штамповки.

Через материал – волочение, прямое и обратное прессование.

Вместе с тем появилась большая группа процессов прессования, в которых силовое воздействие создается инструментом на область пластической деформации, распространяющуюся за пределы конического очага деформации. Поэтому к двум этим группам необходимо добавить еще одну: непосредственно поверхностью инструмента и через материал – прессование с активным действием сил трения, процессы “Конформ”, “Эксторолинг”, “ЛАЙНЕКС” и разработанный на кафедре ОМД СФУ процесс прокатки–прессования [11].

Для процессов первой группы сила (сосредоточенный параметр) определяется по следующей формуле:

,

где s_n – нормальное напряжение на границе контакта; F – площадь контактной поверхности; s_S = s_S(e, x, q) – сопротивление металла пластической деформации, как функция величины деформации e, скорости деформации x и температуры q; s _i – одно из минимальных для рассматриваемого процесса главных напряжений i = 1, 2, 3.

Для процессов второй группы сила определяется по следующим формулам:

P_II = s^*_n F _кj,

когда сила приложена к поперечному сечению получаемого изделия F_к (например, при волочении);

P_II = s^*_n F ₀j,

когда сила приложена к исходному поперечному сечению F₀ (например, при прессовании), причем s^*_n – напряжение, распределенное по поперечному сечению F _к или F ₀, а j = ln.

Для третьей группы появляется новое условие, а именно, вектор сил, создаваемых непосредственно инструментом Р_I должен быть равен или больше требуемого для деформации в коническом очаге деформации при прессовании Р_{I I}. Причем в Р_I должна войти составляющая силы от активного трения

,

а условие устойчивости процесса запишется в следующем виде

.

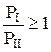Любой процесс протекает во времени, причем для нестационарного процесса P (t, t ₀) изменяется на всем интервале [ t, T ], а для стационарного характерно наличие нестационарной переходной стадии, протекающей в интервале времени [ t ₀, t *]. Если система в момент t ₀ находится в покое, т. е. P⁰ (t)=0 при t ³ t ₀, то ее поведение с момента t ₀ можно описать уравнением

P (t) = R^P (x; t, t ₀) u (t, t ₀, ×), (2.12)

где u(t, t ₀, ×) отражает изменение исходного состояния заготовки в процессе деформации U { u (t, t ₀)| s_s(t, t ₀; e, x, q), v (t, t ₀), q(t, t ₀; x ^a)}, а R^P (x; t, t ₀): U (×)® P; R^P (t, t ₀) – оператор отображения, при этом задание u(t, t ₀, ×) однозначно определит P (t).

Вид, аналогичный уравнению (2.12), будет иметь и уравнение для определения среднего значения нормального напряжения на контактной поверхности

s_n(t) = R ^s(x; t, t ₀) u (t, t ₀, ×) (2.13)

и распределения нормального напряжения на контактной поверхности

s_n(t, x ^a) = R ^s(x; t, t ₀; x ^a) u (t, t ₀, ×).

Уравнения (2.12) и (2.13) представляют линейные отображения

g(P; ×): T ´ T ´ P ´ U ® P,

g(s_n; ×): T ´ T ´s_n ´ U ® s_n.

Оператор R^s для большинства задач находится из решения дифференциального уравнения первого порядка вида y^¢ + p(x)y = q(x) или на основе энергетических методов. В последнем случае (2.12) принимают следующий вид

s_n(t) = å R_i ^s(t, t ₀) u (t, t ₀, ×), i =1, …, n,

где суммирование ведется по составляющим энергетического баланса.

Применительно к процессам ОМД время в уравнениях не присутствует в явном виде, а в качестве параметра обычно выступает изменение какого либо геометрического размера области пластической деформации во времени.

Кроме того, оператор R^s может быть найден из решения дифференциального уравнения в частных производных s_ij,j+r(g_i – w_i)=0.

Для определения состояния Z на основе отображения y(z,x; g(q; ×), ×): T ´ T ´ Z ´ Q ´ Q^T ® Z, математическую модель системы получают путем объединения компонентных и топологических уравнений, базирующиеся на уравнениях движения, равновесия и непрерывности.

Основу таких моделей составляют дифференциальные уравнения

Lz (x ^a) = f (x ^a), (2.14)

где L – дифференциальный оператор; z (x ^a) – зависимая фазовая переменная; x ^a – вектор независимых (пространственных) координат; f (x ^a) – заданная функция.

Нестационарные уравнения в операторной форме запишутся в следующем виде

.

Для области упругой и пластической деформации на основании топологических уравнений – второго закона Ньютона (где – сумма всех сил, действующих на элементарный объем, m – его масса и 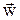– ускорение) и неразрывности , уравнения (2.14) принимают следующий вид

где s_ij – напряжение, действующее вдоль оси x_i в грани элемента, перпендикулярной оси x_j; r – плотность; g_i – компонента вектора заданной распределенной массовой силы; u _i – компоненты вектора перемещения. Напряжения s_ij могут быть связаны как с деформациями e_ij, так и со скоростями деформации x_ij

D _s=b D _e или D _s=b^* D _x,

где D _s, D _e и D _x – соответственно девиаторы напряжений, деформаций и скорости деформации; b и b^* – скалярные множители.

Модели для анализа напряжений и деформаций часто оказываются более удобными, если представлены в интегральной форме, вытекающей из вариационных принципов механики [16,17].

Подходы к решению задач расчета напряженно–деформированного состояния при пластической деформации сегодня достаточно хорошо разработаны как аналитически, так и численно.

Требования на поведение системы обычно накладывают на выходной процесс, например, получение продукта с заданными свойствами. Однако, учитывая связь (1.7), их всегда можно (и это особенно целесообразно при решении задач для выработки определенно направленных воздействий, как для управления, так и для выбора рациональных технологических режимов процессов ограниченных первоначальной настройкой) переформулировать в виде условий, накладываемых на процесс в пространстве состояний.

В общем случае для данных условий модель (1.7) примет следующий вид

y (t) = j(t; t, z (t; ×)).

Поскольку y (t) должна принадлежать заданной области ограничений D_Y, y (t)Î D_Y, то и на z (t; t, ×) должно быть наложено требование принадлежности ограниченной области D_Z, z (t; t, ×)Î D_Z. Размеры области D_Z могут быть определены обратным отображением j^-1

z (t; t, ×)=j^-1 y (t), при y(t) Î D_Y и z (t; t, ×)Î D_Z,

где D_Y ={ y ç y_{i min} £ y_i £ y_{i max} }, i =1, n и D_Z ={ z ½ z_{j min} £ z_j £ z_{j max} }, j =1, m.

Однако множество состояний системы обычно бывает богаче множества Y, в чем проявляется, в частности, сложность системы и её наблюдаемость. Например, зависимость величины зерна от термодеформационных параметров деформирования в общем случае может быть выражена зависимостью

S = S (e, x, q),

где S – величина зерна; e – величина деформации; x – скорость деформации; q – температура деформации.

Структура, например, прессизделий из алюминиевых сплавов является распределенным параметром и обычно неоднородна вследствие неравномерности деформации, изменения температурных условий в течение процесса прессования и последующего охлаждения. Неоднородность структуры проявляется главным образом в изменении зерен уже в прессованном состоянии: в центральных слоях зерна крупнее и уменьшаются при переходе в периферийные слои. Структура изменяется и по длине прессизделия – выходная часть профиля обычно имеет крупнозернистую структуру, ближе к утяжному концу размеры зерен уменьшаются. Таким образом, состояние материала в области пластической деформации существенным образом влияет на состояние прессизделия, характеризуемое распределением структуры по объему.

В работе [21] установлено, что в пространстве параметров e, x и q существует не только отдельная точка, в которой достигается требуемое значение S, но и целая область, которую можно назвать областью устойчивости процесса по параметру заданной структуры (рис. 2.12). В связи с этим необходимо, чтобы из множества значений распределенных по области пластической деформации параметров e, x и q, их максимальные и минимальные значения находились в допустимых технологией производства пределах:

D_Z ={ z ½ e _min£e £ e _max; x _min£x £ x _max; q _min£q £ q _max}.

			C

Модель определения типа структуры запишем в следующем виде

S =W₁ S^I + W₂ S^II + W₃ S^III,

причем

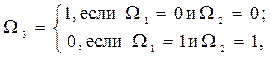
где Q = ax^C уравнения границ раздела областей с заданной структурой. В соответствии с данными [21] из диаграммы структурных состояний сплава АМг6 для применяемых на практике режимов прессования получим следующие уравнения границ W₁: Q=480x^0,05 и W₂: Q=300x^0,023.

При таком подходе пространство состояний разбито на определенное число областей G_i, i =1, k. В каждой области G_i искомая характеристика y =j(z) может быть аппроксимирована как функцией достаточно простого вида, так и многомерным брусом или мажорирована эллипсоидом. Получаемая в результате модель может быть представлена в следующем виде

y (z)=, (2.15)

где

W _i, i=1, …,k – функция принадлежности (соответствия или индикаторная).

Модель в виде (2.15) является достаточно обобщающей и может быть применима для представления целого ряда характеристик функционирования ТП, например, для прогнозирования поврежденности металла при пластической деформации, так на основании работы [22] получим вариант модели следующего вида

где L – степень деформации сдвига; L_p =L_p(s/T; m_s; H; Q) – степень деформации сдвига в момент макроразрушения, зависящая от показателя схемы напряженного состояния s/T, показателя Лоде m_s, интенсивности скорости деформации H и температуры Q; a – коэффициент, значение которого

зависит от физико-химической природы деформируемого металла, термомеханических параметров и характера деформации; W_i – функция принадлежности к i-ой области квазимонотонной деформации.

Применим модель вида (2.15) для моделирования изменения геометрических размеров получаемых изделий. В общем виде изменение геометрического размера изделия h структурно связано с проектным исходным размером инструмента h₀ (зазор между валками, размер канала матрицы и т.п.) и изменениями как инструментального размера Dh_i(z), так и размера изделия Dh_j(z) в зависимости от изменения состояния системы. Тогда уравнение размерной цепи в общем виде можно записать следующим образом

h = h ₀ +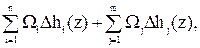

где W_i и W_j принимают значения 0 или ±1 в зависимости от принадлежности к области влияния на уменьшение или увеличение размера. Величины Dh_i(z) и Dh_j(z) являются агрегированными переменными и методика их определения будет рассмотрена ниже.

Основываясь на том, что в условиях высоких требований к точности функционирования ТП, в частности, к точности геометрических размеров, естественно считать все возмущения–факторы малыми отклонениями от номинальных условий обработки и ограничиться линейным приближением. Модель отклонений, например, размеров прессуемых профилей в каждом цикле прессования можно, согласно нашим данным [23], записать в виде (2.15), а именно

D y (z, n)=, (2.16)

где j₁ºh_n – погрешность, обусловленная факторами с последействием, влияние которых проявляется в последующих n+1 циклах обработки; j₂ºw_n – случайная погрешность, порождаемая факторами без последействия, так называемый «белый шум»; j₃º h_nm=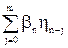– величина погрешности при «затухании» последействия, а m – «память» системы, характеризующая затухания последействия; j₄º F(n) – систематическая погрешность, например, износ; W_i служит индикатором необходимости включения данного вида погрешности, причем W₁= W₃. В данном представлении модель (2.16) характеризует процессы, называемые процессами авторегрессии k -го порядка и скользящего среднего m -го порядка и применима для расчета погрешностей обработки для различных циклических процессов (прессование, штамповка).

Систематическая составляющая изменения размеров при износе или смятии элементов инструмента может быть представлена в следующем виде

F(g)= (2.17)

где g – параметр, характеризующий время работы инструмента; a_j – коэффициенты; W_i – принадлежность к условиям работы инструмента, например, типам применяемых смазок.

Модель (2.17) для износа выходной волоки при волочении биметаллической медно–никелевой проволоки диаметром 0,150 мм при различных условиях работы алмазных волок, построенная нами по экспериментальным данным работы [24], будет иметь следующий вид

D d =[W₁(0,27 g)+W₂(0,117 g)+W₃(0,063 g)+W₄(0,049 g -

- 2,029×10^-3× g ²+2,442×10^-5× g ³)]10^-3,

где D d – износ в мм; g – масса протянутой проволоки в кг; W_i – принадлежность к следующим условиям работы алмазных волок: i =1 – мыльная эмульсия, одинарная волока; i =2 – масло, одинарная волока; i =3 – масло, “напорная волока”; i =4 – масло, напорная трубка (диаметр канала 0,3 мм). Аналогичный вид имеют и модели при износе штампов, по экспериментальным данным [25] износ формообразующих выталкивателей в зависимости от числа отштампованных поковок G в тысячах штук можно записать в следующем виде:

– величина смятия D_см= 0,732 G - 0,035 G ², мм;

– величина истирания D_ист= 17,67G - 9,58 G ² + 1,93 G ³, мм.

Дата добавления: 2014-01-07