Для решения задач ОМД

Пакеты программ методов конечных элементов

Целью решения динамических задачи механики деформируемого тела (динамического анализа) является определение реакции деформируемой механической системы на заданное зависящее от времени возмущение. В результате решения задачи требуется определить перемещения, скорости, ускорения элементов этой системы, напряжения и деформации в них, а также производные от них величины. Важным является то, что при решении задачи учитываются силы инерции, а искомые величины ищутся как функции времени.

В простейшем случае уравнение движения, которое решается при динамическом анализе, может быть записано в следующем матричном виде:

,

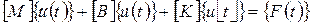где [M], [B], и [K] - матрицы масс, демпфирования и жесткости соответственно; 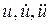- векторы перемещения, скорости, и ускорения; t - время.

При квазистатическом анализе силами инерции пренебрегают. В простейшем случае уравнение квазистатического анализа имеет следующий вид:

.

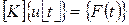При статическом анализе приложенная к системе нагрузка считается стационарной, т.е. не зависящей от времени. В простейшем случае уравнение статического анализа имеет следующий вид:

.

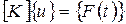Целью решения связанных задач механики деформированного тела и теплопереноса является определение распределения перемещений, скоростей, ускорений элементов рассматриваемой системы, напряжения и деформации в них, а также температуры, тепловых потоков и производных от них величин как функции времени. Связывание осуществляется посредством:

- влияния температуры на характеристики механических свойств материалов, параметры моделей материалов, моделей накопления поврежденности и критериев разрушения;

- учета в расчете напряженно-деформированного состояния рассматриваемой системы температурного расширения;

- учета в расчете теплопереноса работы пластической деформации.

На сегодняшний день существует большое количество коммерческих и некоммерческих программных продуктов и пользовательских алгоритмов математического моделирования, основанных на различных численных схемах и предлагающих пользователю очень широкий спектр возможностей в вычислениях. Подобные программные продукты принято относить к классу CAE[2] систем. В зависимости от широты круга решаемых задач их принято условно разделять на «тяжелые» универсальные и «узкоспециализированные», ориентированные на узкий круг задач программы.

Математический аппарат для расчета процессов обработки металлов давлением находиться на стыке таких дисциплин как МДТТ (механика деформируемого твердого тела) и гидродинамика применительно к вязким веществам. Дело в том, что температурный режим, при котором происходит обработка заготовок находиться в очень широком диапазоне – от 20º С до 1200 º С и иногда может сопровождается локальными перегревами металла до состояния его расплавления.

В связи с этим обстоятельством, а также учитывая сложность каждой из дисциплин – МДТТ и гидродинамики, можно сказать что построение надежных и точных вычислительных алгоритмов для решения задачи пластического деформирования во всем диапазоне температур это сложная задача даже для современного уровня вычислительной математики и техники. Кроме того, если обратить внимание на существенную деталь моделирование процесса ОМД – перестраивание кристаллической структуры металла под действием температур и давлений, становиться очевидным необходимость использования также и полуаналитических методик, которые основаны на большом опыте ОМД. Поэтому знание о вычислительных возможностях современных программных средств попросту необходимо для корректного и адекватного решения сложных задач ОМД.

В настоящий момент существует много пакетов программ, как широко известных так и «закрытых», используемых только внутри производственных компаний, а также тех которые только «зародились» и только развиваются. Общим для всех разработанных методов для решения задач ОМД является использование метода конечных элементов (МКЭ). Мы рассмотрим только те, которые доказали свою пригодность для расчета процессов ОМД.

Самым широко известным и популярным пакетом среди различных специалистов является многоцелевой конечно-элементный расчетный комплекс Ansys Multiphysics c подключенным расчетным модулем LS-DYNA. Расчетный комплекс Ansys зародился в 70 годах 20-го века как многофункциональный комплекс физиков-ядерщиков США для расчета мультифизичных явлений протекающих в агрегатах энергетических станций. Со временем этот пакет постоянно улучшался новыми возможностями, в частности в области моделирования процессов механики и в настоящее время представляет собой мощнейший универсальный инструмент для расчета и исследования процессов. Но сам Ansys Multiphysics не был бы так универсален без расчетного блока LS-DYNA. Дело в том, что сам Ansys Multiphysics развивался как пакет для расчета процессов протекающих с небольшими скоростями и в которых можно пренебрегать диссипативными процессами (нагреванием металла при его деформации), в которых нет большого формоизменения материала (больших пластических деформаций) и нарушения сплошности материала, а также отсутствует хрупкий характер разрушения материалов. В свою очередь пакет LS-DYNA был создан в недрах национальной Ливерморской лаборатории США для моделирования именно быстропротекающих процессов (вплоть до взрывов) с учетом всего многообразия эффектов протекающих в данных процессах. Следует отметить, что Ansys Multiphysics использует неявную схему интегрирования по времени при численном решении, что обеспечивает устойчивость решения, однако требует слишком больших временных затрат, в LS-DYNA же, используется явная схема интегрирования по времени, что обеспечивает быструю скорость решения при наличии большого числа временных шагов решения. Поэтому, сочетание вышеперечисленных пакетов обладает новым качеством – возможностью расчета процессов ОМД и сопутствующих явлений во всем диапазоне скоростей протекания процессов.

Рассмотрим основные функциональные характеристики пакета программ LS DYNA c подключением к Ansys Multiphysics.

Дата добавления: 2014-01-07