Then begin

Begin

if mod(Y,2)=0

X1:=X1*Y;

end;

X2:=X2*Y;

Y:=Y-1;

end;

write(X1);

write(X2);

end Рисунок 4.5.

Программа представляет два различных аспекта процесса: вычисление и управление. Сети Петри удачно представляют структуру и управление программ. Они предназначены для моделирования упорядочения действий и потока информации, а не для действительного вычисления самих значений.

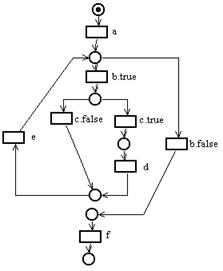Стандартный способ представления структуры программы и потока управления в ней - это блок-схемы, которые в свою очередь могут быть представлены сетями Петри. Блок-схема программы состоит из узлов двух типов (принятия решения, обозначаемых ромбами, и вычисления, обозначаемых прямоугольниками) и дуг между ними. Блок-схема программы изображена на рисунке 4.5, где блоки:

a: read(Y); X1:=1; X2:=1;

b: Y>0

c: mod(Y,2)=0

d: X1:=X1*Y;

e: X2:=X2*Y; Y:=Y-1;

f: write(X1); write(X2);

В сети Петри (рисунок 4.6), моделирующей блок-схему, узлы блок-схемы представляются переходами сети Петри как показано ниже, а дуги блок-схемы — позициями сети Петри. Фишка в сети Петри представляет счетчик команд блок-схемы.

Рисунок 4.6.

4.3.3.2. Моделирование взаимодействия процессов.

Параллельная система может строиться несколькими способами. Один из способов состоит в простом объединении процессов, без взаимодействия во время их одновременного выполнения. Так, например, если система строится этим способом из двух процессов, каждый из которых может быть представлен сетью Петри, то сеть Петри моделирующая одновременное выполнение двух процессов, является простым объединением сетей Петри для каждого из двух процессов. Начальная маркировка составной сети Петри имеет две фишки, по одной в каждой сети, представляя первоначальный счетчик команд процесса.

Такой способ введения параллелизма имеет низкое практическое значение. Далее будем рассматривать параллельные системы процессов, допускающие взаимодействие процессов во время их параллельного выполнения.

Существуют различные виды взаимодействия (синхронизации) процессов, в том числе: взаимодействие посредством общей памяти; - посредством передачи сообщения различных видов.

Таким образом, для моделирования сетями Петри параллельных систем процессов, помимо последовательных процессов, необходимо уметь моделировать различные механизмы взаимодействия (синхронизации) процессов.

Далее покажем, как сети Петри могут моделировать различные механизмы синхронизации процессов, на основе решения с помощью сетей Петри ряда задач, ставших классическими в области синхронизации.

4.3.3.3. Задача о взаимном исключении.

Пусть несколько процессов разделяют общую переменную, запись, файл или другой элемент данных. Для обновления разделяемого элемента данных процесс должен сначала считать старое значение, затем вычислить новое и, наконец, записать его на то же место. Если два процесса P₁ и P₂ в одно и то же время пытаются выполнить такую последовательность действий, то могут возникнуть искажение данных. Например, возможна следующая последовательность:

1. Процесс P₁ считывает значение х из разделяемого объекта;

2. Процесс P₂ считывает значение х из разделяемого объекта;

3. Процесс P₁ вычисляет новое значение х'=f(x);

4. Процесс P ₂ вычисляет новое значение х"=g(x);

5. Процесс P₁ записывает х' в разделяемый объект;

6. Процесс P₂ записывает х" в разделяемый объект, уничтожая значение х

Результат вычисления процесса P₁ потерян.

Для исключения подобных проблем используется метод взаимного исключения, основанный на понятии критическая секция. Критическая секция – это участок кода процесса, на котором он осуществляет доступ к разделяемому объекту данных. Прежде, чем выполнить свою критическую секцию, процесс ждёт, пока другой процесс не закончит выполнение собственной критической секции (если такое выполнение имеет место). Затем он входит в критическую секцию и блокирует доступ для любого другого процесса к своей критической секции. После выполнения процессом критической секции деблокируется доступ для других процессов к разделяемому объекту данных.

Рисунок 4.7.

Следующая сеть Петри (рисунок 4.7) моделирует механизм взаимного исключения для двух процессов P₁ и P₂. Она легко обобщается на произвольное число процессов.

Позиция mпредставляет условие «критическая секция свободна», разрешающее вход в критическую секцию. Попытка процесса P₁ (P₂) войти в критическую секцию осуществляется после помещения фишки в его позицию s₁ (s₂). Такая попытка может увенчаться успехом, если в позиции m содержится фишка. Если оба процесса пытаются войти в критическую секцию одновременно, то переходы t₁ и t₂ вступят в конфликт, и только один из них сможет запуститься. Запуск t₁ запретит запуск перехода t₂, вынуждая процесс P₂ ждать, пока процесс P₁ выйдет из своей критической секции, и возвратит фишку обратно в позицию m.

4.3.3.4. Задача о производителе/потребителе.

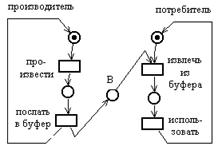В задаче о производителе/потребителе также присутствует разделяемый объект – буфер, посредством которого реализуется взаимодействие через асинхронную передачу сообщений. Процесс-производитель создает сообщения, которые помещаются в буфер. Потребитель ждет, пока сообщение не будет помещено в буфер, извлекает его оттуда и использует. Такое взаимодействие может быть промоделировано сетью Петри, изображенной на рисунке 4.8.

Позиция B представляет буфер, каждая фишка соответствует сообщению, которое произведено, но еще не использовано.

Рисунок 4.8.

4.3.3.5. Задача об обедающих философах.

Напомним, что задача об обедающих философах была предложена Дейкстрой и связана с пятью философами, которые попеременно то гуляли по саду и думали, то ели. За едой философы сидят за круглым столом, в центре которого стояла большая миска спагетти. На столе также лежало пять вилок, по одной между соседними посадочными местами. Для приема употребления спагетти необходимо две вилки. Поэтому каждый философ должен сначала взять вилку слева и вилку справа, а затем приступать к еде. Возможна ситуация, в которой каждый философ возьмет вилку слева, а затем будет ждать, когда освободится вилка с правой стороны. Так они будут ждать, пока не умрут от голода. Тем самым, это состояние системы «обедающие философы» является тупиковым.

Проблема тупика в этой системе может быть решена путем следующей модификации ее правил поведения. Пусть философ при переходе из состояния размышления в состояние приема пищи берет одновременно обе вилки (слева и справа), если они свободны. Сеть Петри (рисунок 4.9) моделирует такую модифицированную систему обедающих философов, свободную от тупиков.

В этой сети Петри позиция п _i, i Î {1,2,3,4,5}, представляет условие «i-тая вилка свободна». В начальной маркировке каждая из этих позиций имеет фишку. Каждому философу i Î {1,2,3,4,5} соответствует две позиции: позиция д _i – представляющая условие «i-тый философ думает»; и позиция е _i – представляющая условие «i-тый философ ест». В начальной маркировке все позиции д _i содержат фишку, а все позиции е _i пусты.

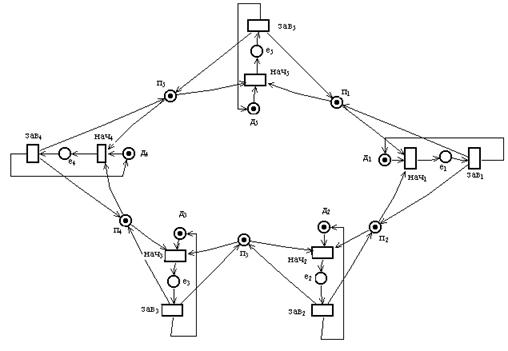Каждому философу i Î {1,2,3,4,5} также соответствует два перехода: переход нач_i – представляющий событие «начало приема пищи i-тым философом»; и переход зав _i – представляющий событие «завершение приема пищи i-тым философом».

Рисунок 4.9.

Дата добавления: 2014-01-07