Переходные процессы под нагрузкой

Общие формулы (5.15) и (5.18) справедливы и для этого случая, вместе с тем различия в характере нагрузки - М_с может быть как активным, так и реактивным - и в начальных условиях делают задачи разнообразными и иногда не очень простыми.

Выясним прежде всего, как будет изменяться правая часть (5.13), т.е. w_с(t) = w₀(t) - М_с / êb½, при тех же, что и прежде, изменениях w₀(t), но различном характере М_с.

Как показано на рис. 5.17, при активном моменте сопротивления w_с(t) располагается ниже w₀(t) на Dw и никаких существенных отличий в алгоритме решения задачи нет. Единственное, пожалуй, о чем следует позаботиться, - о правильном учете начальных условий при пуске. Возможны два случая - первый, когда при t = 0 w = 0, т.е. когда растормаживание привода с активным моментом и начало роста w₀(t) совпадают, и второй, когда до начала пуска привод вращался под действием активного М_с с небольшой скоростью - Dw - пунктир на рис. 5.17.

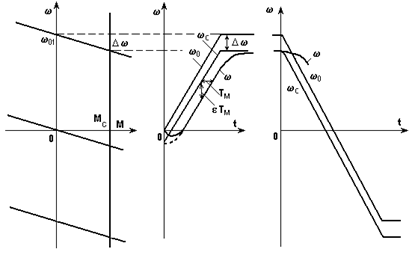
Рис. 5.17. Переходный процесс пуска при активном М_с

При пуске с реактивным М_с (рис. 5.18) скорость начинает изменяться через некоторое время t_з, за которое момент двигателя вырастет до значения М_с. В качестве примера на рис. 5.18 показаны все кривые, соответствующие этому случаю.

Рис. 5.18. Переходный процесс пуска при реактивном М_с

При реверсе с реактивным М_с имеются две ветви w_с(t), причем переход с одной на другую осуществляется в момент времени, когда скорость, достигнув нулевого значения, изменит знак.

Таким образом, как следует из изложенного в системе преобразователь - двигатель можно формировать любые требуемые динамические характеристики.

5.4. Переходные процессы при L¹0

Ограничим рассмотрение задач этой группы случаями, когда механические характеристики привода линейны.

Как и прежде, переходный процесс должен удовлетворять уравнению (5.1)

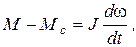
однако изменение М, а значит и 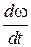теперь будет определяться не только внешним воздействием, но и электрической инерционностью - индуктивностью L. В системе действуют два накопителя энергии J и L и при определенных условиях возможен обмен энергией между этими накопителями, т.е. колебательный процесс.

а) Переходный процесс в электроприводе с двигателем постоянного тока независимого возбуждения при L_я¹0.

Рассмотрим схему на рис. 5.19. Отличительной особенностью схемы по сравнению с рассмотренными ранее является индуктивность L_я. Для якорной цепи справедливо уравнение:

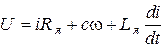, (5.23)

решив которое относительно w:

(*)

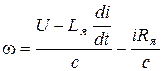и обозначив 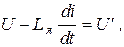получим

. (**)

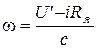Рис. 5.19. Схема пуска электропривода постоянного тока с двигателем

независимого возбуждения

Если сравнить (**) с (3.4), то окажется, что уравнения идентичны, однако в (**) U¢ зависит от 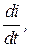т.е. уравнение (**) представляет семейство прямых (рис. 5.20,а), параллельных естественной характеристике и располагающихся как ниже (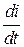> 0), так и выше (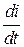< 0) нее. При 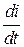= 0, очевидно, уравнение (**) соответствует естественной характеристике.

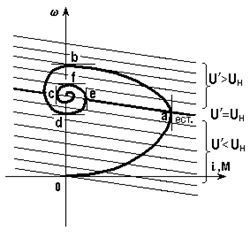
После замыкания ключа К ток i начинает расти, значит растет М и привод разгоняется (для упрощения рассуждений примем М_с = 0), переходя при этом с характеристики на на характеристику (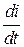> 0, но уменьшается по мере разгона). В процессе увеличения тока и скорости (участок Оа на рис. 5.20) возрастает запас энергии как в индуктивности, так и во вращающемся якоре. В точке а рост тока прекращается; при этом в соответствии с (*) привод оказывается на естественной характеристике, но М > М_с = 0. С точки а начинается спадание тока, т.е. энергия, запасенная в L_я, передается вращающемуся якорю. Механизм передачи очевиден из (*): напряжение, приложенное к якорю U¢, становится больше, чем напряжение сети U. На участке аb привод разгоняется, соответственно растет е = сw, причем в точке b i = 0 - запас энергии в L_я исчерпан, однако w >w₀ и e > U, т.е. в якоре запасена избыточная механическая энергия.

а) б)

Рис. 5.20. Механические характеристики (а) и переходной процесс пуска при L_я ¹ 0 (б)

На участке bc под действием e > U ток изменяет направление, привод тормозится, при этом избыточная механическая энергия вновь переходит в электромагнитную энергию, накапливаемую в индуктивности. В точке с 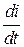= 0, однако в L_я запасена энергия, чему соответствует i ¹ 0 и M ¹ 0. Привод продолжает тормозиться до точки d, затем процесс повторяется.

Кривая 0abcd... w₀ в плоскости w - M представляет собою динамическую механическую характеристику. Соответствующие зависимости w(t), i(t) или M(t) показаны на рис. 5.20,б.

Так как в якорной цепи есть сопротивление R_я процесс перекачивания энергии сопровождается ее рассеиванием, вследствие чего система после ряда колебаний приходит в точку w₀, соответствующую установившемуся режиму. Если бы сопротивление R_я было равным нулю, колебания w и М имели бы незатухающий характер. Если, наоборот, R_я велико, энергии, запасенной в L_я на участке 0а, может оказаться недостаточно для покрытия потерь в R_я и вывода якоря в точку w > w₀ при i = 0. В этом случае процесс будет иметь апериодический характер.

Количественное описание рассмотренных выше процессов можно получить, решив совместно (5.1) и (5.23). Из (5.1) при М_с = 0 следует:

.

Подставив это выражение и его производную

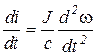
в (5.23), получим после элементарных преобразований:

(5.24)

где

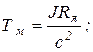
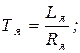
Решение (5.24) найдем в виде

w = w_св + w_пр = 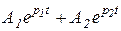+ w₀, (5.25)

где А₁, А₂ - постоянные, определяемые по начальным условиям

w ½ _t=0 и

p₁, p₂ - корни характеристического уравнения

1 + Т_мр + Т_мТ_яр² = 0 (^D)

Решив (^D), получим

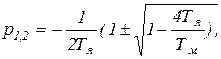
откуда вытекает условие колебательности процесса. Если

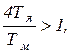т.е. Т_м < 4Т_я,

корни комплексные и процесс носит колебательный характер; если

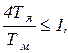т.е. Т_м ³ 4Т_я,

корни действительные и процесс апериодический.

Уравнение для тока или момента легко получить, воспользовавшись, как и прежде, (5.15). Продифференцировав (5.25) и умножив результат на J получим:

М = J (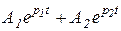). (5.26)

б) Переходные процессы в системе ИТ-Д, замкнутой по скорости

Рассмотрим переходные процессы в системе ИТ-Д (п. 3.7) на участке, где действует отрицательная обратная связь по скорости. Если при анализе установившихся режимов мы не учитывали индуктивность цепи возбуждения, то теперь это сделать необходимо, так как момент в этой системе определяется i_в, а изменение этого тока связано с L_в.

Уравнения динамики для схемы на рис. 5.21 имеют вид (примем, как и в предыдущем случае, что М_с = 0):

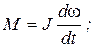(5.27)

(5.28)

где U_в - напряжение на обмотке возбуждения;

R_в, L_в - активное сопротивление и индуктивность цепи возбуждения;

i_в - текущее значение тока возбуждения.

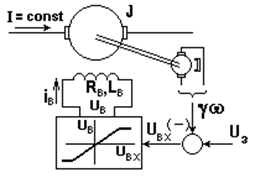
Рис. 5.21. Схема системы источник тока – двигатель, замкнутой

по скорости

Эти уравнения отражают динамические свойства системы, так как содержат члены члены с J и L_в. Кроме того, следует записать уравнения, отражающие связи между переменными.

Из общего уравнения для момента (3.1), приняв, что Ф = a i_в, имеем:

М = kФI = kI a i_в

или с учетом (5.27)

Из уравнения замыкания системы при линейном безынерционном возбудителе получаем:

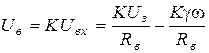
или с учетом (5.28)

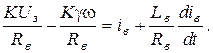
После простых преобразований получаем окончательно:

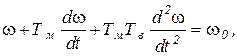(5.29)

где 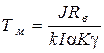- электромеханическая постоянная времени;

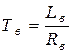- постоянная времени цепи возбуждения;

- скорость идеального холостого хода.

Сравнив (5.29) с (5.24), обнаруживаем полное сходство уравнений, хотя входящие в них параметры совершенно различны. В этом факте проявляется глубокая физическая общность систем на рис. 5.19 и 5.21: каждая из них имеет по два накопителя энергии и существуют условия для обмена энергией между ними.

Очевидно, что уравнению (5.29) соответствуют процессы, рассмотренные в п.а).

в) Переходные процессы при изменении магнитного потока двигателя независимого возбуждения.

Рис. 5.22. Схема электропривода постоянного тока с двигателем

независимого возбуждения при ослаблении поля

Рассмотрим еще один практически важный случай - изменение Ф в двигателе постоянного тока независимого возбуждения (рис. 5.22). В исходном состоянии ключ К замкнут и привод работает на естественной характеристике (рис. 5.22) в точке w_нач = w_{с нач}. Переходный процесс вызывается размыканием в момент t = 0 ключа К, в результате чего уменьшается ток i_в и магнитный поток Ф и привод переходит на верхнюю характеристику. Если бы обмотка возбуждения не обладала индуктивностью, то ток i_в изменился бы мгновенно, т.е. мгновенно исходная (естественная) характеристика заменилась бы конечной, и переходный процесс протекал по ней, как было описано в п.5.2 (пунктирные стрелки на рис. 5.23). В действительности же L ¹ 0, и переход от естественной характеристики к конечной происходит во времени, причем темп этого перехода в общем случае соизмерим с темпом изменения скорости. В результате динамическая механическая характеристика имеет вид, показанный на рис. 5.23 сплошной линией со стрелкой.

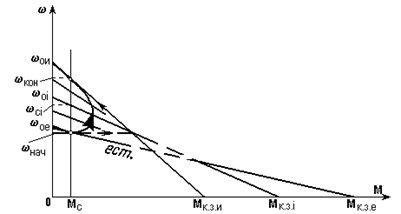
Рис. 5.23. Механические характеристики при ослаблении поля

Получим уравнение, описывающее изменение скорости. Для этого за основу, как и раньше, возьмем уравнение движения 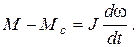(5.1)

(5.1)

Зависимость момента от скорости можно в соответствии с рис. 5.23 записать как

. (*)

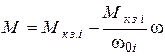Подставив (*) в (5.1), после простых преобразований получим

или, если учесть, что

и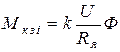

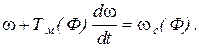(5.30)

В этом уравнении, похожем внешне на (5.6), есть существенное отличие: Т_м и w_с зависят от потока и растут с его уменьшением.

В свою очередь, магнитный поток экспоненциально изменяется во времени, если принять зависимость Ф(i_в) линейной.

Численное решение (5.30), подстановка в (5.1) и вычисление тока якоря по соотношению

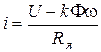
приводят к результату, представленному на рис. 5.24 и имеющему, как и при всяком численном решении, частный характер.

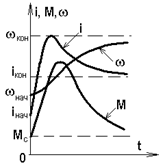
Рис. 5.24. Переходный процесс при ослаблении поля

В данном случае переходной процесс определяется двумя инерционностями - J и L_в и описывался двумя дифференциальными уравнениями первого порядка, одно из которых было нелинейным. Эти уравнения не имели комплексных корней, в чем отразилась физическая невозможность обмена энергией между двумя накопителями.

Дата добавления: 2014-01-07