Определение объема выборки при работе с выборочными долями

В приведенных выше примерах речь шла о средних. Однако многих заказчиков исследований интересуют другие параметры, например, выборочной доли p. В нашем примере может вызвать интерес определение доли лицензии рыболовов, прибывших из других мест, или проживающих в сельской местности, или рыболовов, выезжающих с ночевкой. В рассмотренных методах речь шла о трех вещах, необходимых для определения объема выборки: определенном доверительном уровне, определенной точности и знании характера распределения выборочной статистики. Определение первых двух величин обусловлено спецификой постановки проблемы. Абсолютная точность, хоть и выраженная в процентном отношении, означает, что оценка будет находиться в интервале, определенном в долях истинного значения, например, в пределах ± 5% от истинного значения. Теперь остается рассмотреть распределение выборочных долей.

Среднеквадратическая ошибка доли определяется (формула 1.7):

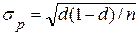, (1.7)

где d – выборочная доля;

σ_p - среднеквадратическая ошибка доли;

n – объем выборки

В этом случае средним значением является генеральная доля, а среднеквадратическим отклонением – среднеквадратическая ошибка доли. Отсюда объем выборки определяется по формуле (1.8):

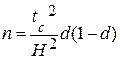, (1.8)

Например, предположим, что необходимо узнать долю всех рыболовов, которые в течение года хотя бы раз выезжали на рыбалку с ночевкой. Предположим также, что нужно произвести оценку этой доли с точностью ± 2% и доверительным уровнем 95% (t_c=2). Тогда,

.

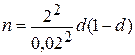Данное уравнение содержит два неизвестных: оцениваемую долю признака в генеральной совокупности и объем выборки. Поэтому необходимо оценить первое значение и определить объем выборки, используя эту оценку. Для того, чтобы провести предварительную оценку, необходимо обратиться к данным предыдущих исследований, либо провести предварительное обследование. Если в силу каких-то причин невозможно ни то, ни другое, можно провести оценку параметра на основе компетентного правдоподобного суждения. Следствием неточной оценки может стать увеличение или уменьшение точности доверительного интервала. Например, если исследователь принял долю рыболовов, выезжавших на рыбалку с ночевкой, равной 20%, то в этом случае объем выборки составит:

.

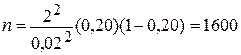Представим, что после обследования выборки, состоящей из 1600 рыболовов выборочная доля (р) оказалась равной 0,40. Величина доверительного интервала будет зависеть от выборочной среднеквадратической долевой ошибки S_p, которая в данном случае подменяет собой неизвестную среднеквадратическую долевую ошибку генеральной совокупности s_p (формула 1.9):

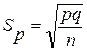, (1.9)

где p – доля единиц выборки; q=1-p.

В нашем примере

.

Доверительный интервал для доли признака в генеральной совокупности определяется как выборочная доля p± ts_p= 0,40±2(0,012) или 0,376 £ d £ 0,424.

Однако, интервал оказался шире заданного. Причина состоит в том, то выборочная доля оказалась больше расчетной доли признака в генеральной совокупности.

Т.к. объем выборки прямо пропорционален произведению d(1-d), то произведение максимально при d=0,5. Поэтому в отсутствии какой-либо информации о доле признака в генеральной совокупности можно принимать d=0,5. При этом точность доверительного интервала возрастет в той же мере, в какой выборочная оценка будет отличаться от принятого значения, равного 0,5.

Необходимо отметить, что во всех выше приведенных расчетах по определению объема выборки генеральная совокупность не входит в формулу расчета, т.е., с оговоркой можно сказать, что объем выборки не зависит от генеральной совокупности.

Объясняется это тем, что если все элементы генеральной совокупности имеют одно и то же значение количественного признака (например, все рыболовы тратят на питание и проживание по $74 в год), то для определения среднего достаточно будет отобрать выборку, состоящую из одного-единственного элемента. При этом количество элементов в исходной совокупности может равняться 1000, 10000 или 100000. что действительно оказывает влияние на объем выборки, так это степень изменчивости количественного признака. Чем выше степень изменчивости признака, тем большим должен быть размер выборки, обеспечивающей заданную точность исследования. Например, если наш район (область, страна) изобилует рыбой, привлекающей рыболовов и из других стран, то при определении среднего расстояния, преодолеваемого рыболовами во время их туров, можно столкнуться с огромным разбросом значений этой величины.

Итак, объем генеральной совокупности оказывает на объем выборки лишь опосредованное влияние. В большинстве случаев с возрастанием объема исходной совокупности возрастает и потенциальная возможность увеличения изменчивости исследуемого количественного признака.

Объем выборки не зависит от объема генеральной совокупности и при оценке доли. Для доли определяющим фактором является расчетная доля генеральной совокупности, обладающая данным признаком: чем ближе эта доля к 0,5, тем большей должна быть выборка, при этом ее объем не зависит от объема всей совокупности. Значение 0,5 соответствует максимальной изменчивости, т.к. половина генеральной совокупности обладает данным признаком, а половина не обладает им.

Выше приведенные ситуации имеют отношение к тем, где целевая совокупность представляется, по сути, бесконечно большой (например, исследование потребительских товаров). В тех случаях, когда выборка представляет собой бо^/льшую часть генеральной совокупности, во избежание переоценки выборки требуется некоторое изменение формул расчета. И в первую очередь, это связанно с тем, что с увеличением объема выборки возрастает и стоимость исследования. В связи с этим в формулу вводят коэффициент поправки на конечность совокупности (N-n)/(N-1). Тогда формула расчета среднеквадратической ошибки среднего имеет следующий вид (формула 1.10):

, (1.10)

где N – объем генеральной совокупности.

Когда требуемая выборка составляет более 5% генеральной совокупности, ее расчетный объем должен быть уменьшен путем ввода в формулу поправки на размер совокупности (формула 1.11):

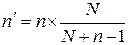, (1.11)

Например, генеральная совокупность состоит из 100 элементов, а оценка требуемого объема выборки составляет 20 элементов, при использовании указанной поправки исследованию должно подлежать меньшее число элементов. Требуемый объем выборки n^/=nN/(N+ n-1), где n – первоначальное, а n^/ - пересмотренное значение объема выборки. Так, для N=100 и n=20 на деле можно обследовать только 17 элементов.

Дата добавления: 2014-01-07