Осаждение частиц под действием силы тяжести

Внешняя задача гидродинамики

Законы движения твердых тел в жидкости (или обтекание твердого тела жидкостью) имеют важное значение для расчета многих аппаратов, применяющихся в технологии строительных материалов. Знание этих законов позволяет не только более полно представить физическую сущность явлений, происходящих, например, при транспортировании бетонных смесей по трубопроводам, перемешивание различных масс, движение частиц при сушке и обжиге во взвешенном состоянии, но и более правильно и экономично сконструировать технологические аппараты, применяемые для этих целей.

При движении тела в жидкости (или при обтекании неподвижного тела потоком жидкости) возникают сопротивления, для преодоления которых и обеспечения равномерного движения тела должна быть затрачена определенная энергия. Возникающее сопротивление зависит, главным образом, от режима движения жидкости и формы тела.

При ламинарном режиме, имеющем место при небольших скоростях и малых размерах тел или при высокой вязкости жидкости, тело окружено пограничым слоем жидкости и плавно обтекается потоком (рис. 6.1,а).

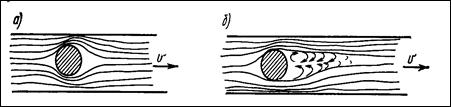
Рис. 6.1. Движение твердого тела в жидкости:

а – ламинарный поток; б – турбулентный поток

Потеря энергии в таких условиях связана в основномс преодолением сопротивления трения.

С развитием турбулентности потока (например, с увеличением скорости движения тела) все большую роль начинают играть силы инерции. Под действием этих сил пограничный слой отрывается от поверхности тела, что привовдит к понижению давления за движущимся телом в непосредственной близости от него и к образованию беспорядочных местных завихрений в данном пространстве (рис. 6.1,б). При этом разность давлений жидкости на переднюю (лобовую) поверхность тела, встречающую обтекающий поток, и на его заднюю (кормовую) поверхность все больше превышает разность давлений, возникающую при ламинарном режиме движения. Начиная с некоторого значения критерия Рейнольдса, роль лобового сопротивления становится преобладающей, а сопротивлением трения можно практически пренебречь. В данном случае наступает автомодельный (по отношению к критерию Рейнольдса) режим движения.

Сопротивления давления и трения в общем случае существуют одновременно, и полное сопротивление, которое возникает при относительном движении тела и жидкости, представляет собой сумму этих сопротивлений:

, (6.1)

где Р_давл – сопротивление давления; Р_тр – сопротивление трения.

Соотношение между этими слагаемыми различно в разных случаях.

Полное сопротивление определяется по формуле Ньютона:

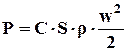, (6.2)

где C – коэффициент сопротивления среды; S – площадь проекции тела на плоскость, перпендикулярную направлению его движения; w – скорость движения; r - плотность жидкости.

При движении тел, отличающихся по форме от шара, коэффициент сопротивления среды зависит от критерия Рейнольдса (от режима движения) и от фактора формы Ф, т.е. C = f(Re, Ф).

Фактор формы определяется по соотношению:

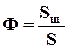, (6.3)

где S_ш – поверхность шара, имеющего тот же объем, что и рассматриваемое тело; S – поверхность рассматриваемого тела.

Законы движения двухфазных жидкостей (жидкость плюс взвесь твердых частиц) имеет большое значение в инженерной практике. В промышленности строительных материалов взвесенесущие потоки применяют при пневмотранспорте цемента, гидротранспорте бетонных смесей, сушке и обжиге сыпучих материалов во взвешенном состоянии др. технологических процессах.

Основные вопросы, интересующие инженера, - определение необходимой скорости транспортирования и потерь давления.

Особенности взвесенесущих потоков в значительной степени определяются характером обтекания твердых частиц потоком жидкости или газа. Пусть в вертикальной трубе диаметром D (рис.6.2) движется сферическая частица диаметром d (D >> d). Поток среды направлен снизу вверх. На частицу действует сила давления P, направленная снизу вверх, и сила тяжести G.

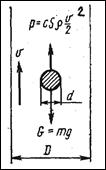
Рис. 6.2. Схема сил, действующих на частицу, находящуюся в восходящем потоке

В зависимости от соотношения этих сил частица может подниматься, опускаться или оставаться неподвижной. Условие равновесия будет наблюдаться при P =G. Это случай витания частицы.

Сила тяжести сферической частицы в жидкой среде определяется соотношением:

, (6.4)

где r_т – плотность частицы; r_ж – плотность жидкости.

Уравнение равновесия частицы имеет вид:

, (6.5)

откуда скорость витания частицы (скорость потока, при которой частица будет находиться в равновесии):

. (6.6)

В случае воздушных потоков с достаточной для инженерных расчетов точностью можно принять (r_т - r_ж)» r_т, т.к. плотность воздуха очень мала по сравнению с плотностью твердого тела. В этом случае скорость витания частицы определяется по формуле:

(6.7)

В реальных взвесенесущих потоках необходимо в эти формулы внести поправки для учета влияния стенок трубы и соседних частиц:

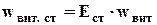(6.8)

где Е_ст – коэффициент стеснения, зависящий от соотношения d/D и объемной концентрации частиц в потоке.

Таким образом,

· Тело в потоке жидкости будет находиться в состоянии равновесия (витать), если скорость витания равна скорости потока жидкости (w_вит = w);

· Тело будет двигаться по направлению движения жидкости, если скорость жидкости больше скорости витания частицы (w_вит < w);

· Тело будет осаждаться под действием силы тяжести, если скорость витания частицы больше скорости потока (w_вит > w).

В системах пневмотранспорта для надежного перемещения материалов скорость движения воздуха обычно в 1,5-2 раза превышает скорость витания.

Максимальный размер частиц, осаждение которых происходит по закону Стокса, можно определить из соотношения:

, (6.9)

где h - вязкость жидкости.

При Re £ 10^-4 и когда d становится соизмеримым с длиной среднего свободного пробега молекул l, на скорость осаждения очень мелких частиц начинает влиять тепловое движение молекул среды, приводящее к отклонению от закона Стокса. В этом случае в формуле (9) используется поправочный коэффициент K = f(l/d).

Практика показывает, что при d» 0,1 мкм пыль, находящаяся в воздухе, не осаждается, а наблюдается броуновское движение частиц.

Дата добавления: 2014-01-07