Пересчет характеристик насоса

Критерий подобия Фруда

В тех случаях, когда движение жидкости является безнапорным и происходит под действием разности нивелирных высот, условие подобия потоков описывается иначе, с помощью другого критерия подобия - числа Фруда. Этот критерий учитывает пропорциональность в отношениях сил инерции к силам тяжести. Однако для подавляющего большинства интересующих нас задач в области машиностроения этот критерий не имеет значения и рассматриваться не будет.

Заключение о подобии напорных потоков

Итак, в подобных напорных потоках имеем равенство безразмерных коэффициентов и чисел α, ζ, λ, Eu, Re, Ne. Изменение Re означает, что меняется соотношение основных сил в потоке, в связи с чем указанные коэффициенты могут также несколько меняться. Поэтому все эти коэффициенты следует рассматривать как функции Re (хотя в некоторых интервалах Re они могут оставаться постоянными).

Движение жидкости в проточной части лопастных насосов имеет достаточно сложный характер, поэтому при разработке и создании современных гидромашин необходимо проводить испытания в лабораторных и натурных условиях. Такие исследования опираются на использование общей теории гидромеханического подобия движения реальной жидкости.

Геометрическое подобие, как известно из геомет­рии, представляет собой пропорциональность сходственных раз­меров и равенство соответствующих углов. В гидравлике под геометрическим подобием понимают подобие тех поверхностей, которые ограничивают потоки, т. е. подобие русл или каналов. При моделировании два насоса могут считаться подобными, если линейные размеры одного из них (модель) в одинаковое число раз меньше соответствующих размеров другого:

При геометрическом подобии все углы постоянны. Для пол­ного геометрического подобия необходимо, чтобы относительная шероховатость D/D и относительные зазоры d/ D) были одинаковы для обоих насосов.

Кинематическое подобие означает пропорциональ­ность местных скоростей в сходственных точках и равенство углов, характеризующих направление этих скоростей. Траекто­рии движения должны быть геометрически подобны:

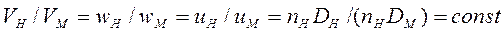
Динамическое подобие— это пропорциональность сил, действующих на сходственные объемы в кинематически подобных потоках, и равенство углов, характеризующих направ­ление этих сил. Динамическое подобие сводится к равенству чисел, или критериев Эйлера, Рейнольдса, Фруда:

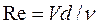
две l — характерный линейный размер; t — время.

Гидромеханическое подобие основывается на со­блюдении геометрического, кинематического и динамического подобия.

Критерии будут определяющими тогда, когда они выражены через исходные величины, задаваемые в начальных и граничных условиях.

В практике моделирования гидромашин большое значение имеет критерий Эйлера:

Пересчет характеристик насоса при изменении частоты враще­ния и диаметра рабочего колеса. Для пересчета характеристик воспользуемся формулами закона пропорциональности:

при наружном диаметре рабочего колеса D₂ = const.

Пересчет осуществляется следующим образом: задают ряд значений расхода Q, по имеющейся характеристике находят со­ответствующие каждому значению Q напор Н и КПД. Под­ставляют найденные значения Q₁, п₁ и H в уравнение и получают соответствующие значения Q₂, h₂ и H₂, т. е. координа­ты точек новой характеристики насоса при частоте вращения n₂. Наносят точки на график и получают искомую характеристику насоса при n₂.

Если дана зависимость Н от Q при n₁ = const., то аналогичная кривая для n₂ ⁼ const может быть получена пересчетом абсцисс точек (подач) первой кривой пропорционально отношениям час­тот вращения, а ординат (напоров) — пропорционально квадрату этого отношения. Таким путем можно получить целую серию характеристик одного и того же насоса для ряда разных частот вращения n₂, n₃, n₄ и т. д.

На практике, если подобрать центробежный насос по каталогу или с применением закона динамического подобия не удается, прибегают к обточке его рабочего колеса. Практика и проведен­ные испытания показали, что при допустимом уменьшении диа­метра колеса КПД насоса снижается мало, но довольно сильно изменяются подача и напор. Необходимую степень обточки ко­леса определяют таким образом, чтобы удовлетворить расчетным значениям подачи и напора. Максимальная степень обточки ко­леса центробежного насоса зависит от быстроходности и воз­можна в следующих пределах: для n _s = 60… 120—на 20...15 %, для n _s = 120...200 — на 15...10, для n _s = 200...300 — на 10...5 %.

Дата добавления: 2014-01-07