Абсолютные, относительные и средние величины

Использование поправочных коэффициентов.

В условиях рыночных отношений в качестве поправочных коэффициентов используются индексы цен. С их помощью осуществляется перерасчет стоимостных показателей из фактических в сопоставимые. С этой целью показатель, который необходимо привести в сопоставимый вид умножают или делят (в зависимости от базового уровня, к которому приводят показатель) на индексы потребительских цен цепным методом. (Умножаем, если приводим к отчетному году, делим – к базисному).

Количественная определенность показателей выражается в абсолютных и относительных величинах. Абсолютные показатели отражают количественные размеры яв­ления в единицах меры, веса, объема, продолжительности, площа­ди, стоимости и т.д. безотносительно к размеру других явлений, а относительные – соотношение величины изучаемого явления и величины какого-либо другого явления или величины этого явле­ния, но взятой за другой период или по другому объекту.

Относительные показатели получают в результате деления од­ной величины на другую, которая принимается за базу сравнения. Это могут быть данные плана, базисного года, другого предприятия, среднеотраслевые и т.д. Относительные величины выража­ются в форме коэффициентов (при базе 1) или процентов (при базе 100).

Виды относительных величин:

· относительные величины планового задания;

· относительные величины выполнения плана;

· относительные величины динамики;

· относительные величины структуры;

· относительные величины координации;

· относительные величины интенсивности;

· относительные величины эффективности.

Относительные величины координации представляют собой со­отношение частей целого между собой, например активной и пас­сивной частей основных производственных фондов, силовых и рабочих машин, собственного и заемного капитала и т.д.

Относительные величины интенсивности характеризуют степень распространенности, развития какого-либо явления в соответству­ющей среде, например степень заболеваемости персонала, процент рабочих высшей квалификации и т.д.

Относительные величины эффективности – это соотношение эффекта с ресурсами или затратами, например размер прибыли на рубль затрат, на одного рабочего, на рубль выручки, на рубль вло­женного капитала и т.д.

Наряду с абсолютными и относительными показателями применяются средние величины для обобщенной количественной характеристики сово­купности однородных явлений по какому-либо признаку. Напри­мер, средняя зарплата рабочих используется для обобщающей ха­рактеристики уровня оплаты труда изучаемой совокупности рабо­чих.

В АХД применяют разные типы средних величин (табл. 4)

При использовании средних величин в АХД следует учитывать, что они дают обобщенную характеристику явлений, основываясь на массовых данных.

Таблица 4 –Виды и порядок расчета средних величин

Вид средней величины	Порядок расчета	Область применения
Средняя ариф­метическая простая	, где х1, х2,…., хп - варианты показа­теля; п - число вариантов	Используется в тех слу­чаях, когда все варианты возникают один раз или имеют одинаковые частоты в исследуемой совокуп­ности
Средняя ариф­метическая взвешенная	где х1, х2,..., хп - варианты показа­теля, f1, f2,...,f n - общая числен­ность каждого варианта; ∑ fi - об­щее число единиц совокупности	Используется в тех случаях, когда варианты показателя повторяются неодинаковое количество раз
Средняя гео­метрическая	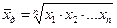где п - число вариантов (коэф­фициентов роста), которое будет на единицу меньше числа членов динамического ряда	Используется для исчисле­ния средних темпов роста исследуемых показателей в динамике
Средняя хроно­логическая	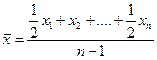где х1, х2,.., хп - уровень показате­ля на определенную дату; п - число дат	Исчисляется по показа­телям, значения которых заданы в форме дискрет­ных величин, варьирующих во времени
Среднее квадратическое отклонение		Применяется для оценки степени варьирования исследуемых показателей относительно среднего их уровня

Дата добавления: 2014-01-07