Введение. подисциплине 5483 (Эконометрика)

ТЕКСТ ЛЕКЦИИ

ЛЕКЦИЯ № 2

подисциплине 5483 (Эконометрика)

ТЕМА «Сущность метода наименьших квадратов (МНК) и его предпосылки: построение уравнений парной линейной регрессии»

Обсуждена на заседании кафедры

(предметно-методической секции)

«___»___________2007г.

Протокол № __

МГУПИ – 2007г.

Тема лекции: «Cущность МНК и его предпосылки: построение уравнений парной линейной регрессии»

Учебные и воспитательные цели:

1. Ознакомление студентов с математическими основами метода наименьших квадратов

2. Изучение сущности метода наименьших квадратов (МНК)

3. Усвоение способа построения уравнений парной линейной регрессии с помощью МНК

Время: 2 часа (90 мин.).

Литература (основная):

1. «Эконометрика», под редакцией Елисеевой И.И., М., «Финансы и статистика», 2005г

2. Елисеева И.И., Курышева С.В., Гордеенко Н.М., Бабаева И.В., Костеева Т.В., Михайлов Б.А., «Практикум по эконометрике», Изд-во «Финансы и статистика», Москва, 2004.

Литература (дополнительная):

3. Тихомиров Н.П., Дорохина Е.Ю., «Учебно-методическое пособие по дисциплине «Эконометрика», Изд-во РЭА., Москва, 2004.

4. Кремер Н.Ш., Путко Б.А., «Эконометрика: Учебник для вузов», ЮНИТИ-ДАНА, Москва, 2004.

5. Доугерти К., «Введение в эконометрику», Инфра-М, Москва, 2004.

Учебно-материальное обеспечение:

1. Наглядные пособия: раздаточный материал в виде плакатов

2. Технические средства обучения: электронный конспект лекций

ПЛАН ЛЕКЦИИ:

Введение – до 5 мин.

Основная часть (учебные вопросы) – до 80 мин.

1-й учебный вопрос: Математические основы МНК - 25 мин.

2-й учебный вопрос: Сущность МНК и его предпосылки – 25 мин.

3-й учебный вопрос: Построение уравнения парной линейной регрессии – 20 мин.

4й учебный вопрос: Интерпретация параметров уравнения парной регрессии – 10 мин

Заключение – до 5 мин.

Сегодня мы изучим основной метод, который используется для построения эконометрических моделей – метод наименьших квадратов. Суть данного метода кратко рассматривалась в курсе теории статистики.

Но ранее мы его рассматривали очень упрощенно, в основном, как способ построения уравнений тренда и простейших уравнений регрессии. Сегодня мы рассмотрим математические основания этого метода, теоретические предпосылки, которые положены в его основу, и его использование на примере построения уравнений парной линейной регрессии. В дальнейшем мы рассмотрим более детально особенности уравнений множественной линейной регрессии.

1й учебный вопрос. Математические основы метода наименьших квадратов.

Ранее (в курсе теории статистики) мы уже отмечали, что любое уравнение регрессии представляет собой уравнение некоторой математической функции, приближенно описывающее статистическую зависимость между показателями. Постановку задачи выбора наиболее подходящей функции рассмотрим на примере уравнения парной регрессии.

Пусть у нас есть набор значений двух переменных: x_t, y_t, t=1,2,..., n. Предположим, что задачей является подобрать функцию y=f(x) из параметрического семейства функций f(x, α), наилучшим образом описывающую зависимость y от x. Поиск функции данного типа означает практически, что нужно выбрать "наилучшее" значение параметра α.

В качестве меры отклонения функции f (x, α) от набора наблюдений можно взять:

- сумму квадратов отклонений, т.е.

;

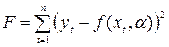- сумму модулей отклонений, т.е.

;

- или в общем случае

,

где g - "мера", с которой отклонение 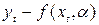входит в функцию F.

Достоинства и недостатки перечисленных функционалов:

Дата добавления: 2014-01-07