Минимальные покрытия множеств функциональных зависимостей

Попытаемся теперь выяснить, какова роль F -зависимостей в реляционных базах данных. Как показали исследования, класс F -зависимостей оказывает существенное влияние на построение согласованных схем реляционных баз данных, определяет механизмы согласованности данных и целостности баз данных.

Одной из основных целей создания базы данных является сохранение всех данных и взаимосвязей между ними из предметной области в вычислительной среде. Табличное представление отношений в реляционных базах данных позволяет выдвинуть следующую гипотезу хранения данных - каждой ФЗ по отношению. Другой целью создания базы данных является надежность и целостность сохраняемых данных. Можно предположить, что табличное представление породит ряд проблем, связанных с восстанавливаемостью данных, и вступит в противоречие с требованием производительности базы данных. Поэтому меньшее число F-зависимостей означает меньший объем использования памяти компьютера и меньшее число проверок при операциях модификации.

В начале проектирования реляционных баз данных всегда возникает задача представления множеств F -зависимостей. Чем меньшим числом отношений их можно представить, тем лучше. Формализация решения этой задачи строится на понятии покрытия ФЗ. Построение покрытий множеств ФЗ является четвертой (4) конструктивной идеей в теории проектирования реляционных баз данных. Введем ряд определений.

Определение 11. Два множества F-зависимостей F и G над схемой r отношения R эквивалентны, если их замыкания совпадают, т.е. F⁺ = G⁺.

Эквивалентность двух множеств ФЗ F и G устанавливается следующим образом: для каждой ФЗ из F проверяется ее принадлежность G⁺; для этого вычисляется Y⁺; затем проверяется вложение Z в Y⁺; если каждая зависимость F принадлежит G⁺, то каждая зависимость в F⁺ принадлежит G⁺; далее повторяем процедуру для G по отношению к F.

Следствием введения понятия эквивалентности является следующий важный факт: каждое множество ФЗ покрывается некоторым множеством ФЗ, в которых ни одна из правых частей не имеет более одного атрибута (правила декомпозиции и объединения). Таким образом, существует набор эквивалентных схем для каждой исходной схемы отношений реляционной базы данных.

Теория проектирования реляционных баз данных дает возможность построения более коротких представлений ФЗ. Для рассмотрения таких процедур введем понятия неизбыточных ФЗ и минимального покрытия множеств ФЗ.

Определение 12. Множество F -зависимостей F неизбыточно, если у него нет собственного подмножества, эквивалентного ему самому.

Определение 13. Множество F -зависимостей F минимально, если оно содержит не больше F-зависимостей, чем любое эквивалентное ему множество.

Минимальное покрытие (МП) не может содержать избыточных зависимостей. Понятие МП F можно детализировать следующим образом:

• правая часть каждой ФЗ в F содержит один атрибут;
• ни для какой ФЗ 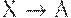из F множество 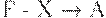не эквивалентно F;
• ни для какой ФЗ 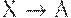из F и собственного подмножества 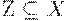множества 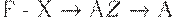не эквивалентны.

Доказано, что для каждого множества ФЗ F существует эквивалентное ему минимальное покрытие. Для заданного F может существовать несколько минимальных покрытий. Ниже приведены общие алгоритмы проверки избыточности и построения минимальных покрытий.

Алгоритмы проверки избыточности

Алгоритм REDUNDANT (F)input: Множество Foutput: True, если F избыточно 1. temp = false for any X ->Y < F do if MEMBER (F - { X -> Y }, X -> Y) then temp = True Return (temp) Алгоритм NONREDUN (G)input: Множество ФЗ Goutput: Неизбыточное покрытие G 1. F = G for any X ->Y > G do if MEMBER (F - { X -> Y }, X -> Y) then F = F - { X -> Y } Return (F)

Алгоритмы построения минимального покрытия

Алгоритм MINIMAZE (G)input: Множество ФЗ Goutput: Минимальное покрытие G F = NONREDUN (G) Построить непустые множества Еf(X)⁺, состоящие из ФЗ, с левой частью, эквивалентной Х. Ef(X) - подмножество Ef(X)⁺, отвечающее атрибуту Х. for any Ef(X) из Ef(X)⁺ do for any Y -> U из Ef(X) do for any Z -> V <> Y->U из Еf(X) do if DDERIVERS (F, Y, -> Z) then заменить Y->U и Z->V на Z->UV в F Return(F)

Примеры. Построение минимального покрытия ФЗ

Пусть F = {AB -> C, C -> A, BC -> D, ACD -> B, D -> EG, BE -> C, CG -> BD, CE -> AG}.

Расщепив правые части с помощью правила декомпозиции, получим

AB -> C, C -> A, BC -> D, ACD -> B, D -> E, D -> G, BE -> C, CG -> B, CG -> D, CE -> A, CE -> G}.

CE -> A - избыточна, так как следует из C -> A.

CG -> B - избыточна, так как следует из CG -> D, C -> A, ACD -> B.

Больше избыточных ФЗ нет.

ACD -> B может быть замещена CD -> В, так как C -> A.

Первое МП:

AB -> C, C -> A, BC -> D, CD -> B, D -> E, D -> G, BE -> C, CG -> D, CE -> G.

Построим второе МП, исключив CE -> A, CG -> D, AC -> DB:

AB -> C, C -> A, BC -> D, D -> E, D -> G, BE -> C, CG ->В, CE -> G

Так же как и для F -зависимостей, можно определить правила вывода для многозначных MV -зависимостей, и определить их взаимоотношения с F -зависимостями, а далее показать совместную полноту правил вывода F - и MV -зависимостей.

Правила вывода для MV-зависимостей:

• Дополнение. Если 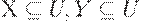и задана МФЗ , то имеет место МФЗ .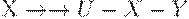
• Пополнение. Если 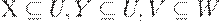и задана МФЗ X Y, то имеет место МФЗ .
• Транзитивность. Если 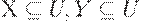и заданы МФЗ и МФЗ , то имеет место МФЗ .
• Объединение. Если 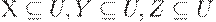и заданы МФЗ и МФЗ , то имеет место МФЗ .
• Псевдотранзитивность. Если 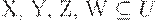и заданы МФЗ и МФЗ 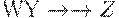, то имеет место МФЗ .
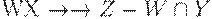• Смешанная транзитивность. Если 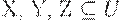и заданы МФЗ и ФЗ , то имеет место ФЗ .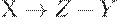
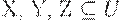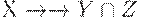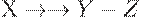• Декомпозиция. Если и заданы МФЗ и МФЗ то имеют место МФЗ , МФЗ , МФЗ .

Совместные правила вывода для F - и MV -зависимостей:

1. Если 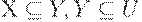и задана ФЗ , то имеет место МФЗ .
2. Если 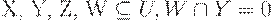и заданы МФЗ и ФЗ , то имеет место ФЗ .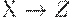

Справедливо следующее утверждение: система правил вывода F1-F3, MV1-MV3, FMV1 и FMV2 является надежной и полной.

Правила декомпозиции и объединения MV -зависимостей позволяют сформулировать следующее утверждение. Пусть U - множество атрибутов, тогда можно построить разбиение U-X на множества , такое, что при имеет место МФЗ , если только Z является объединением некоторого числа Y_i. Набор множеств Y₁, Y₂,..., Y_k называется базисом Х F - и MV -зависимостей. Каждое Y_i может состоять из одного атрибута.

Пусть D - множество F - и MV -зависимостей, тогда, так же как и для F-зависимостей, замыкание D⁺ множества D может быть логически выведено по аксиомам F1-F3, MV1-MV3, FMV1 и FMV2. Однако этот процесс может потребовать времени, пропорционального e^L, где L - число ФЗ в D.

На практике часто требуется только знать, следует ли из D конкретная ФЗ или 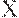. Этого достаточно, чтобы исключить избыточные ФЗ. Для того чтобы определить, имеет ли место MV -зависимость , достаточно построить базис Х зависимостей и посмотреть, является ли Z - X объединением каких-либо его множеств. Для вычисления базиса зависимостей Х относительно D достаточно найти базис относительно множества МФЗ М, где М состоит из а) всех МФЗ из D и б) множества МФЗ для каждой ФЗ в D, где .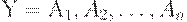

Ниже приведен алгоритм вычисления базиса Х ФЗ относительно M.

Алгоритм вычисления базиса функциональных зависимостей

input: Множество MV-зависимостей М на множестве атрибутов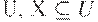

output: Базис Х относительно М.

1. Пусть Т - множество множеств 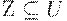, таких, что для некоторой МФЗ в M имеем , и Z есть либо Y - X, либо U - X - Y.
2. До тех пор, пока Т не превратится в совокупность непересекающихся множеств, будем искать в нем очередную пару пересекающихся множеств Z¹, Z² и заменять ее множествами , отбрасывая пустое множество . В результате получим множество S.
3. До тех пор, пока возможны изменения во множестве S, будем искать МФЗ 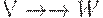в М и некоторое множество Y в S, такие, что Y пересекается с W, но не пересекается с V. Заменяем Y в S на и Y - W.
4. Полученная совокупность множеств S есть базис Х ФЗ.

Теория функциональных зависимостей на отношениях реляционной базы данных представляет собой математический фундамент, на котором строится проектирование реляционных баз данных. Подытожим сведения о функциональных зависимостях, полученных в данном учебном элементе.

• Аксиомы вывода ФЗ позволяют производить формальное (алгебраическое) манипулирование зависимостями разных классов: F- и MV -зависимостями. В рамках данных аксиом преобразования схем отношений реляционных баз данных будут эквивалентными.
• Аксиомы вывода ФЗ позволяют оперировать отдельными атрибутами зависимостей, при этом сами ФЗ сохраняются: атрибуты из правой части ФЗ могут быть удалены; атрибуты из левой части ФЗ могут быть удалены, если удаляемый атрибут отсутствует в правой части; независимо от того, перекрываются ли множества атрибутов или нет, любые атрибуты из исходного множества можно одновременно подставлять в правую и левую части ФЗ. Несущественные зависимости могут быть удалены, а затем восстановлены.
• Существует минимальный набор ФЗ, который позволяет восстановить исходный набор ФЗ. Это обстоятельство позволяет теоретически обосновать и практически проводить эквивалентные, сохраняющие семантический смысл данных, преобразования схем отношений реляционной базы данных.

Дата добавления: 2014-01-07