Проверка прочности трубопровода

После определения толщины стенки и продольных напряжений по формуле (8.41), осуществляют проверку прочности трубопровода по формуле

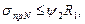
где 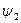- коэффициент, учитывающий двухосное напряженное состояние металла труб, при растягивающих осевых продольных напряжениях (s _{пр. N} ³ 0) принимаемый равным единице, при сжимающих (s _{пр. N} < 0) определяемый по формуле

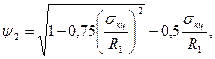(8.55)

.

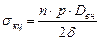Если необходимо ограничить (предотвратить) недопустимые пластические деформации подземного и наземного в насыпи трубопровода проверку проводят по второму предельному состоянию, по которому деформации трубы ограничены нормативным пределом текучести 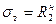. В этом случае проверку проводят по условиям

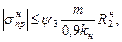(8.56)

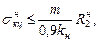(8.57)

где m – коэффициент условий работы трубопровода;

k_н – коэффициент надежности по назначению;

R₂^н – нормативное расчетное сопротивление, значение которого равно пределу текучести стали 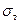для труб по ГОСТ и ТУ;

k₂ =0,9 – коэффициент надежности по материалу (СНиП 2.05.06-85);

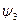- коэффициент, учитывающий двухосное напряженное состояние металла труб; при растягивающих продольных напряжениях (s ^н _{пр. N} ³ 0) принимаемый равным единице, при сжимающих (s ^н_{пр. N} < 0) - определяемый по формуле

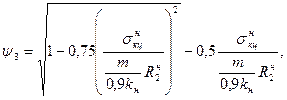(8.58)

где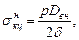

s ^н _{пр. N} – максимальное суммарное продольное напряжение от нормативных нагрузок и воздействий.

Выполнение этих условий обеспечивает местную устойчивость стенок трубы и не допускает накопление пластических деформаций (обеспечивается долговечность).

Необходимо отметить, что по второму предельному состоянию продольные напряжения определяются с учетом изгиба трубопровода для крайних волокон сечений трубы, исходя из упругой работы металла.

В СНиП 2.05.06-85 приведена формула для определения максимальных продольных напряжений для частного случая упругого изгиба трубы, при воздействии внутреннего давления p и температурного перепада Δ t

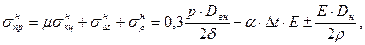(8.59)

где 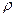– минимальный радиус изгиба оси трубы.

В формуле (8.59) третье слагаемое соответствует выражению для напряжений в поперечном сечении трубы при упругом изгибе (8.10).

Используя это выражение и второе предельное состояние определяем ρ_min в случае σ_пр<0.

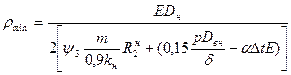и в случае σ_пр.N>0, ψ₃=1

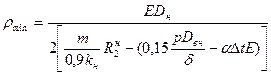
Если использовать выражение σ_пр.N≤ψ₂R₁

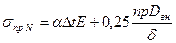
Можно определить предельное допустимое состояние, температурный перепад, невызывающий необходимости увеличения δ.

При положительном перепаде (сжатие):

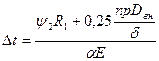
При отрицательном перепаде (растяжение):

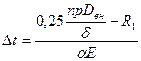
На основании анализа опубликованных работ и проведения экспериментов для определения предельного сопротивления грунта сдвигу рекомендуется следующая формула:

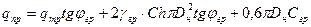, где

q_тр – вес трубопровода с продуктом;

φ_гр – угол внутреннего трения грунта;

γ_гр – объемный вес грунта;

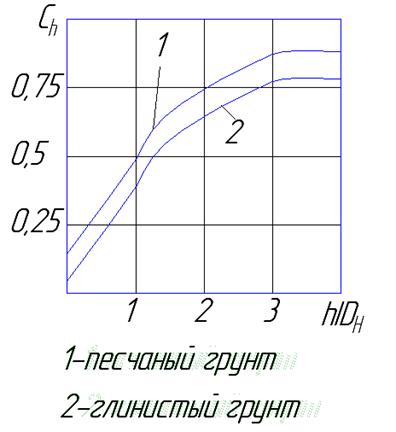
C_h – безразмерный коэффициент, учитывающий образование свода обрушения;

C_гр – сцепление грунта, МПа (характеристика грунта, зависит от коэффициента пористости).

Или вычисляется:

· для песчаного грунта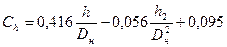

· для глинистых грунтов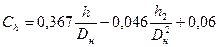

Продольные перемещения подземного трубопровода.

Подземные МТ рассчитывают в зависимости от характеристик среды, в которой они будут находиться при эксплуатации. Они определяются на основе инженерных изысканий трассы.

Деформации в прямых стержнях при растяжении.

Если ось стержня прямая линия и нагружение направлено вдоль нее – отсутствуют изгиб.

Математическая модель содержит: уравнение равновесия, геометрические соотношения и закон Гука.

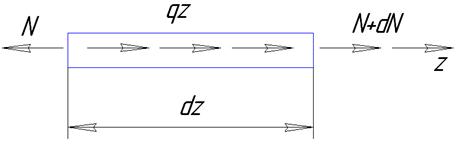
Уравнение равновесия элемента стержня – проекция сил на ось z:

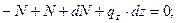
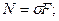
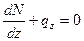
В соответствии с гипотезой плоского сечения перемещение плоского сечения перпендикулярного оси является функцией одной переменной.

Геометрическое соотношение. Формула Коши.

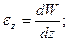
Относительная деформация:

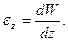
Закон Гука при одноосном напряженном состоянии (НС):

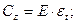
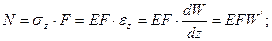
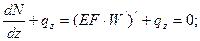
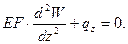
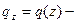интенсивность распределенной вдоль оси нагрузки;

W(z) – находим двукратным интегрированием.

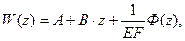где

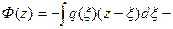функция, зависящая от заданной нагрузки q(z).

A и B – постоянн. опр. из граничного условия.

Для сосредоточенной нагрузки:

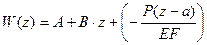
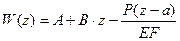
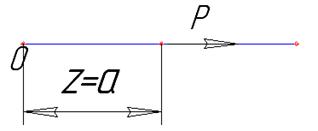
Для распределенной нагрузки: q=const.

.

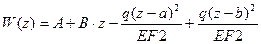Если стержень находится в линейной упругой среде, препятствующий перемещением.

Если жесткость среды С, то 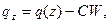а уравнение принимает вид

;

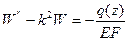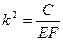
Такая математическая модель может быть использована для определения продольных перемещений МТ в случае линейной модели грунта (простейший случай).

Эта модель впервые предложена профессором Флориным – сопротивление грунта прямо пропорционально продольным перемещениям.

Исследования показали – применима для малых перемещений – для больших существенная нелинейность между С и W.

Чтобы повысить точность расчетов на практике применяют нелинейную модель.

Для определения зависимостей сопротивления грунта – продольное перемещение, проводят эксперименты и строят диаграммы.

Пример эксперимента. Сквозь изучаемый грунт перемещают отрезок трубы (вдоль его оси) и с помощью динамометра определяют силу сопротивления грунта.

По оси абсцисс откладывают продольные перемещения отрезка трубы, как недеформируемого тела, по оси ординат – среднее значение.

Сопротивление грунта сдвигу по периметру трубы.

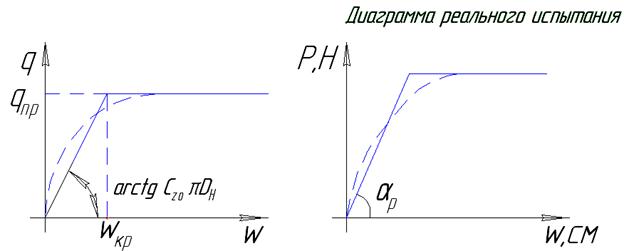
На диаграмме можно выделить 3 участка:

1 – между перемещением и сопротивлением, почти линейная зависимость. Это первая фаза напряженного состояния грунта – фаза уплотнения, когда грунт уплотняется и приобретает свойства упругого тела.

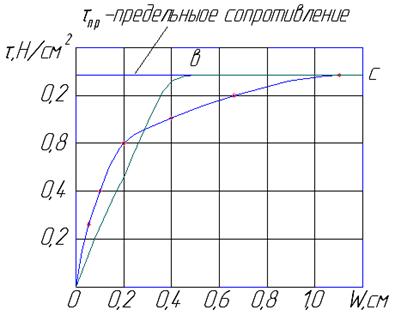
2 – нарушается пропорциональность W-τ, доля упругих деформаций уменьшается, остаточные деформации нарастают.

3 – почти прямая линия, которая характеризует равномерное перемещение отрезка трубы. Характеризует работу грунта в стадии предельного равновесия – между трубой и грунтом устанавливается пластическая связь (описывается свойством пластического тела Прандтля-Кулона).

Для того, чтобы максимально упростить решение полученной математической модели на практике зависимости сопротивления грунта от продольного перемещения можно линеаризировать, т.е. заменить двумя прямолинейными участками.

Второй участок параллелен оси абсцисс и определяется τ=τ_пр – предельное сопротивление грунта.

На первом участке в области упругопластинчатых деформаций зависимость описывается уравнением прямой: 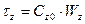, где

C_z0 – обобщенный коэффициент касательного сопротивления грунта (коэффициент постели грунта при продольных перемещениях), tgα=C_z0.

Для определения C_z0 (зная τ_пр) используют условие минимума ошибки: ломаную 0вс проводят таким образом, чтобы площади, образованные экспериментальной кривой и ломаной линией были равны.

Рассмотрим прямоугольный подземный участок трубопровода, правый конец которого неподвижен. Будем считать, что длина его ограничена и равна 1.

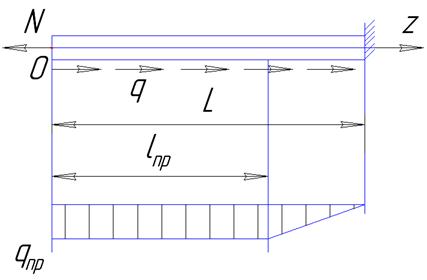
Расчетная модель МТ – стержень трубчатого сечения, взаимодействующий со средой.

Взаимодействие со средой будем считать в соответствии с идеализированной диаграммой Прандтля.

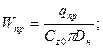
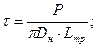
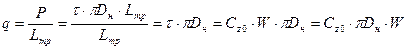, где L_тр – длина отрезка трубы.

Полученная диаграмма учитывает огранич. по величине реакций продольных связей.

Аналитическое выражение модели грунта:

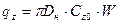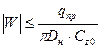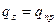при ;

при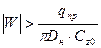

В зависимости от нагрузок и относительной жесткости трубопровода возможны 2 варианта:

• только в упругой стадии W≤W_пр;
• существуют 2 участка.

Участок, где при взаимодействии трубопровода с грунтом q_z=q_пр называется участком предельного равновесия l_пр (первый участок I),

На этом участке 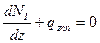при ;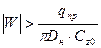

На втором участке (II) 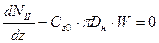при .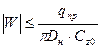

При получении выражения для продольных деформаций необходимо учитывать температурные деформации и деформации от внутреннего давления.

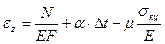, где

E – модуль упругости;

F – площадь кольцевого сечения трубы;

Α – коэффициент линейного расширения материала МТ;

Δt – температурный перепад, положителен при нагреве;

μ – коэффициент Пуассона;

σ_кц – кольцевое давление.

Из полученного выражения получаем

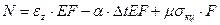
С учетом соотношения Коши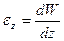

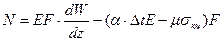
С учетом уравнений равновесия получаем выражения для продольных перемещений W.

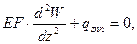
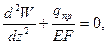
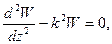
Получим линейные однородные уравнения II-го порядка с постоянными коэффициентами.

Для получения решения 1-го уравнения дважды интегрируем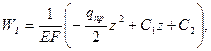

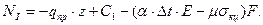
Для второго уравнения характеристическое уравнение: λ₂-k₂=0, λ_1,2=±k

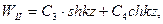
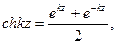
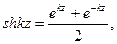
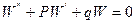
Характеристическое уравнение: λ²+pλ+q=0.

Общее решение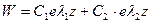

Любая линейная комбинация этих функций будет также решением однородного уравнения.

Метод Эйлера: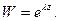

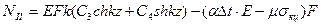
Решение практических задач – определение постоянных C₁-C₄.

Рассмотрим случая, когда имеется l_кр при z=0 N=N₀; z=l_кр W_I=W_II, N_I=N_II,

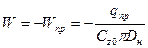(*), z=L, W_II=0.

Пять условий позволяют определить постоянные и l_пр.

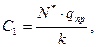
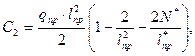C₁=N₀-N_беск,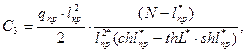

C₄=-C₃ ^. thL^*, .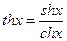

Величину l_кр определим, решая трансциндетное уравнение относительно l_кр*.

(**)

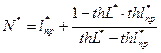Безразмерные параметры:

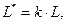
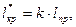
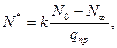
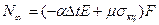
Если уравнение n-ой степени, то алгебраическое 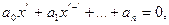неалгебраические уравнения – трансциндетные.

После определения l_кр определяем произвольные постоянные C₁-C₄, которые позволяют определить W_I, N_I, W₂, N₂.

Также определяются продольное перемещение в начале участка W₀ и продольное усилие N_L в конце участка.

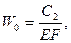
Далее рассматриваем частные случаи. Один из наиболее распространенных, когда можно считать участок трубопровода полубесконечным L→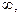thL^*→1.

,

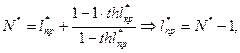
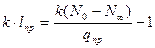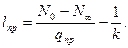
Постоянные: C₁=N₀-N_беск, .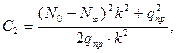

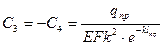Перемещения в начале участка:

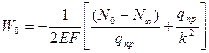
Усилия в защищенной части трубопровода, где W=0.

,

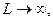
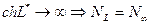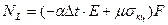
Необходимо ввести критерий – когда размер участка можно считать бесконечно длинным.

Примем условие: перемещение правого конца участка=1% от перемещения сечения, соответственно концу участка предельного равновесия.

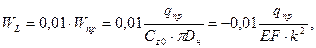
Подставляя в уравнение для W_II, W_II=W_L при z=L, определим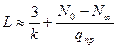

Нужно не забывать, что полученные решения относятся к варианту 2^х участков по длине трубопровода. Чтобы правильно выбрать вариант решения, нужно иметь критерий наличия участка предельного равновесия грунта. Анализируя (**), определим условие l_кр>0.

.

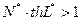Тогда для полубесконечного участка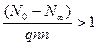

Второй случай участок предельного равновесия отсутствует (критерии не выполняются).

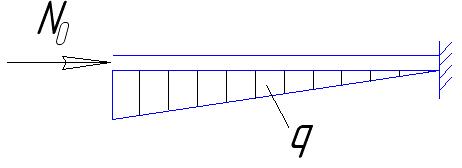
Начальный параметр z=0, N=N₀

Уравнения для W и N аналогичны участку II предыдущей задачи.

.

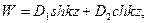
Произвольные постоянные D₁ и D₂ определяются из граничных условий z=0, N=N₀, z=L, W=0.

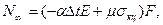z=0, shk ^. 0=0, chk ^. 0=1.

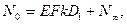
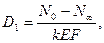z=0, W=0,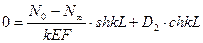

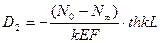
Теперь можно определить W₀ и N_L

,

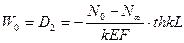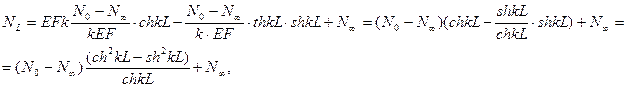
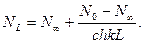
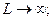
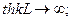
Для полубесконечного участка 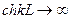используют аналогичный критерий.

Тогда длина участка (который можно принимать) .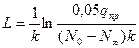

Полученные решения позволяют рассмотреть ряд практически важных конструктивных задач.

1. Определение перемещений в месте выхода подземного участка трубопровода на поверхность.

Если на открытом участке имеются компенсаторы (П, Z или Г-образные) или надземные переходы арочного типа, то можно считать, что отпор этих конструкций пропорционален перемещению. Осевое усилие от внутреннего давления в месте стыка труба – компенсатор равно произведению давления на площадь трубы в свету F_св. Тогда начальный параметр 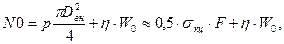где

F – площадь поперечного сечения трубы.

.

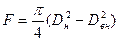Если участок можно считать полубесконечным, то используя уравнение 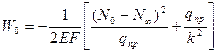можно определить продольное перемещение в месте примыкания его к открытой части трубопровода. Кроме того, определяется дополнительный распор Н и длина подземного участка L на котором происходит это перемещение.

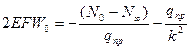подставим N₀ и N_беск

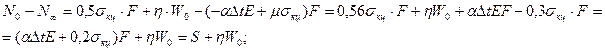
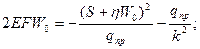
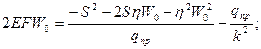
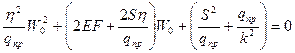
Получаем приведенные квадратные уравнения:

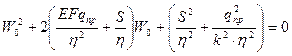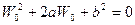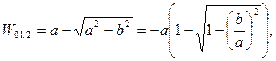, , где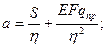

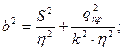
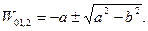
Дополнительный распор H=ηW₀.

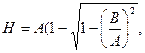где A=ηa, B²=η²b², – длина участка.

При отсутствии участка предельного равновесия грунта, те же величины определяются по формулам:

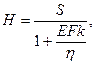
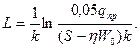
Для различных типов конструкционных примыканий к подземным участкам, жесткость определяется методами сопротивления материалов или строительной механики (метод сил или перемещений).

Для примера рассмотрим вариант, когда в месте выхода подземного МТ находится компенсатор.

Жесткость компенсатора η можно определять в соответствии с нормами СНиП 2.05.06-85 Магистральные трубопроводы.

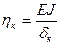
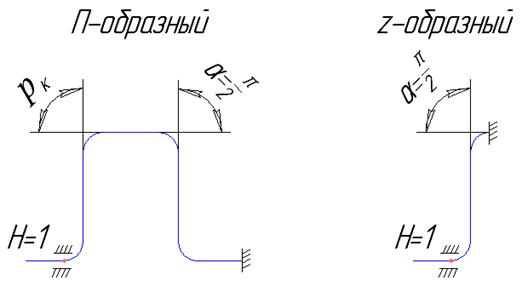
Тогда для П-образного компенсатора δ_к=A, где

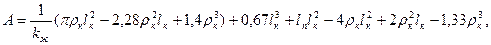
Параметр A определяется по формуле (49).

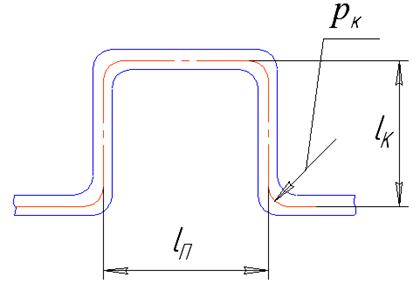
ρ_к – радиус изгиба оси отвода;

l_к – вылет компенсатора;

l_п – ширина полки компенсатора;

k_ж – коэффициент уменьшения жесткости отвода.

Для Г-образного компенсатора .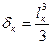

Для Z-образного компенсатора 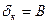(СНиП 2.05.06 формула (51)).

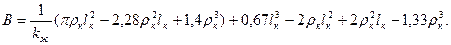
Необходимо подчеркнуть: перемещение W₀ в месте стыка зависит от жесткости компенсатора (параметры l_к, l_п, ρ_к), которые в свою очередь подбираются в зависимости от продольных перемещений и продольных сил, которые возникают от Δt^оС и внутреннего давления.

Поэтому на практике параметры компенсаторов подбирают методом последовательных приближений.

В начале жесткость компенсатора принимается η_к=0 и определяются W₀. Исходя из необходимости компенсировать перемещения определяют параметры и далее жесткость компенсатора.

Далее вычисляют W₀ с учетом η_к.

Таким образом, после нескольких приближений определяют параметры компенсатора.

Наименьшее значение P при n=1.

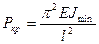– формула Эйлера.

При других условиях закрепления концов стержня получаем более общую формулу для P_кр.

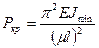, где

μl – привед. дл. ст.;

μ – коэффициент приведения дл.

(**)

,

.

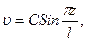
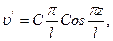
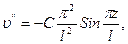
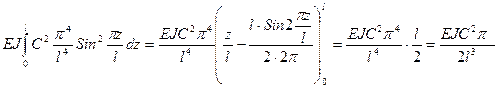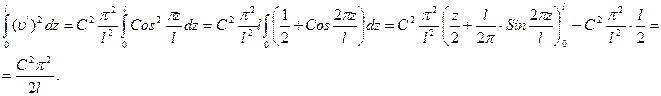
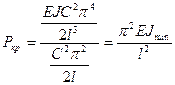Лекция 8, 9.

Устойчивость магистральных трубопроводов.

Понятие потери устойчивости прямого стержня под действием осевой сжимающей силы (сопротивление материалов, с 138…).

Равновесие сжатого стержня может быть устойчивым и неустойчивым.

Устойчивые – выведенные из состояния равновесия, стремится возвратится в первоначальное состояние после сжатия внешней нагрузки.

Неустойчивые – деформированное тело, выведенное из состояния равновесия, продолжает деформироваться в направлении отклонения и после прекращения воздействий в исходное состояние не возвращается.

Между этими состояниями – критические состояния.

Критическая нагрузка – равносильно разрушению конструкции, т.к. неустойчивая форма равновес. обязательно будет утрачена из-за неограниченного роста деформаций и напряжений.

Разрушение происходит внезапно от изгиба, когда прочность элемента на сжатие еще далеко не исчерпана.

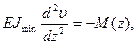
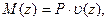
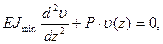
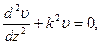где 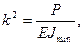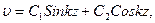где C₁ и C₂ определяют из граничных условий, в частности z=0, υ=0, z=l, υ=0, 0=C₁Sink ^. 0+C₂Cosk ^. 0→C₂=0, 0=C₁Sinkl, С₁≠0, Sinkl=0→kl=nπ²→k²l²=n²π²,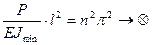

Положительное Δt и внутреннее давление – возникает продольное сжимающее усилие, которое может привести к потере устойчивости. И как наиболее вероятный вариант выпучивания подземного МТ.

Продольная устойчивость будет зависеть в том числе от глубины залегания МТ.

Рассмотрим заглубленный МТ под действием эквивалентного сжимающего усилия (Δt, P).

Для прямолинейной формы (как для сж. ст) уравнение поперечных υ перемещений (прогибов) в линейно упругой сре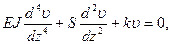де:

где

EJ – изгибная жесткость трубы;

S – эквивалентное сжимающее усилие;

K=C_y0 ^. D_н – коэффициент пропорциональности,

C_y0 – обобщенный коэффициент нормального сопротивления грунта.

Однако, на практике для получения точного решения необходимо учитывать начальное искривление МТ. Выпучивания происходят, хотя имеется запал прочности для прямолинейного трубопровода).

Если рассматривать МТ в вертикальной плоскости с выпуклостью вверх, то можно принять билинейную модель грунта, учитывающую ограниченность сопротивления поперечных перемещений.

Сопротивление грунта поперечным перемещениям трубы.

Наиболее важное перемещение вверх.

Эксперимент: трубы диаметром 273, 529, 720 мм, L=4м.

Трубы поднимали лебедками с помощью тросов. Перемещение υ измеряется прогибомером Максимова.

Опыты при различной высоте засыпки грунта под трубой (от 0 до 100 см).

Грунт нескольких видов.

Общий вид диаграмм во всех испытаниях аналогичен.

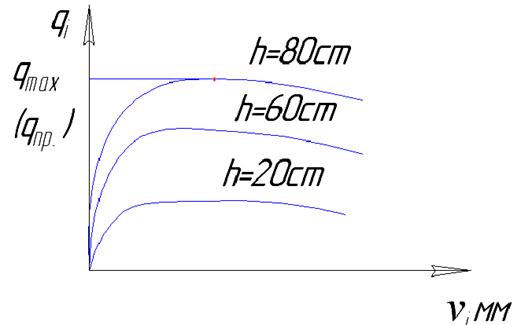
I – пока υ небольшие между сопротивлениями грунта q и υ завис. почти линейна. После q_max происходит снижение сопротивления грунта. Зависимость между q и υ на участке кривой, характеризующей работу грунта:

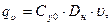где

C_υ0 – коэффициент нормального сопротивления грунта

На основании обработки результатов эксперимента получена эмпирическая зависимость для C_y0.

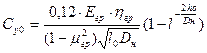, где

E_гр – модуль деформации грунта ненарушенной структуры;

η_гр – коэффициент снижения модуля деформации грунтовой засыпки по сравнению с грунтовой ненарушенной структурой;

μ_гр – коэффициент Пуассона;

l₀ – единичная длина трубы (lo=100 см);

D_н – наружный диаметр трубопровода;

h₀ – расстояние от верха засыпки до оси трубы, см.

Предельная удерживающаяся способность грунта определяется призмой выпора. Для реального трубопровода можно считать, что во всех случаях угол откоса призмы определяется углом внутреннего трения грунта.

На основании экспериментальных данных рекомендуется формула:

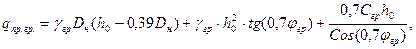где

γ_гр – объемный вес грунта;

D_н – наружный диаметр;

h₀ – от верха засыпки до оси трубы;

φ_гр – угол внутр. тр. грунта;

C_гр – сцепление грунта.

Методы определения основных показателей грунта СНиП II-9-78

Инженерные изыскания для строительства.

Основные положения.

Потеря устойчивости грунта – сопротивление грунта уменьшается по сравнению с max.

При υ величиной порядка высоты засыпки происходит разрушение грунта над трубой.

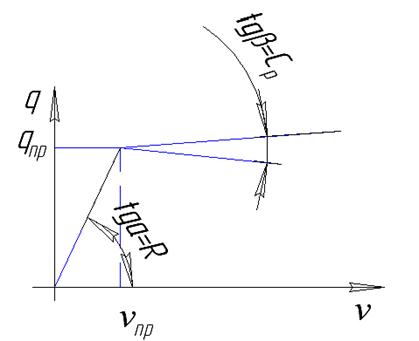
Если считать сопротивление грунта на втором участке (выше предельного) подчиняется линейной зависимости и что при υ=H (глубина заложения):

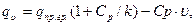(при υ>υ_пр), где

C_p – коэффициент разгрузки, C_p=q_пр.гр./H;

K=C_y0 ^. D_н;

H – расстояние от верха засыпки до низа трубы

Принижаем аналитическую зависимость сопротивления грунта поперечных перемещений:

,

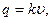
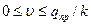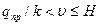
Поставленную задачу можно решить энергетическим методом: анализ полной эн. Трубопровод-грунт. Задаемся формой волны выпучивания (формы начального изгиба и дополнительных перемещений совпадают).

Для первого участка грунта:

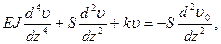где

υ₀ и υ – начальные и дополнительные прогибы в сечении.

Для второго участка грунта диаграммы модели грунта (билинейная модель):

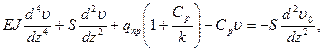где

Так как k>>C_p (см. диаграмму) C_p/k – пренебрегаем.

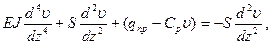
Энергетический метод определения критической силы.

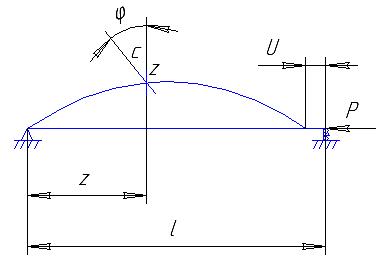
Из курса сопротивления материалов известно, что энергия деформации изогнутого стержня выражается через изгибающий момент:

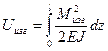. С учетом, что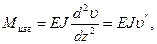

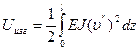
Перемещение λ определяется как разность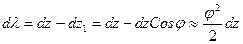

Но при малых прогибах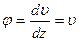

Исходя из этого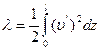

Энергетический баланс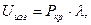

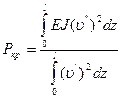
Этот метод позволяет определить P_кр, если задать функцию υ(z) удовлетворяющую граничным условиям. Например:

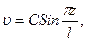
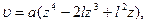
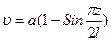или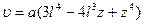

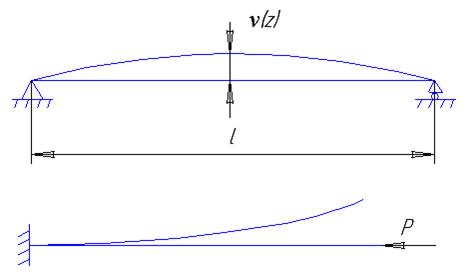
Полная энергия Э=U-W, где

U – потенциальная энергия деформации;

W – работа внешних сил на возможное перемещение.

δЭ=δU-δW=0,

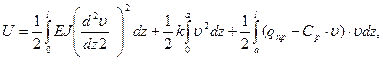
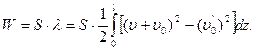
Полная энергия системы трубопровод-грунт для расчетной схемы (*):

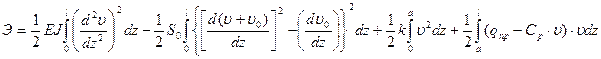
Здесь для интенсивного поперечного напряжения принятый множитель ½ так как эти напряжения при переводе балки из нагруженного состояния в первоначальное →0.

При исследовании устойчивости трубопровода с учетом билинейности диаграммы сопротивления грунта – перемещение считают, что начальная форма прогиба совпадает с формой выпучивания.

Учитывая, что жесткость грунта засыпки значительно меньше жесткости основания, и анализируя случаи выпучивания трубопроводов, можно принять, что при перемещении трубопровода в вертикальной плоскости образуется одна волна выпучивания, примыкающие участки остаются прямолинейными, а по концам волны угол поворота и изгибающий момент равны нулю, т.е. 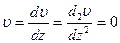при z=0, z=L.

Чтобы определить полную энергию Э необходимо задать форму начального изгиба:

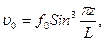
тогда дополнительные поперечные перемещения распределяются по аналогичному закону:

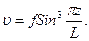
Форма начальной волны совпадает с формой выпучивания трубопровода в процессе деформации и что единственным наперед заданным параметром является стрела начального прогиба f₀.

Подставив уравнения начального и дополнительного прогибов и проинтегрировав, получаем выражение для полной энергии.

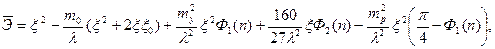где

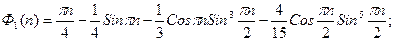
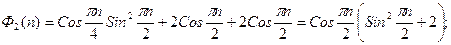
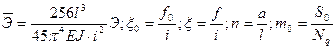– параметр продольного усилия;

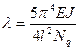– параметр длины выпучивания участка;

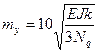– характеристика упругой работы грунта;

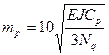– характеристика зоны разгрузки.

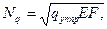
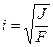– радиус инерции.

Относительная длина участка упругой работы грунта определяется из условия υ(z=a)=q_пр/k.

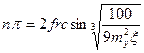
Начало возможных перемещений применительно к деформируемому телу формируется следующим образом: в состоянии равновесия возможная работа внешних сил равна приращению потенциальной энергии деформации.

δU=δW.

Начало возможных перемещений можно записать в виде вариационного уравнения Лагранжа.

δЭ=δ(U-W)=0.

Вариационное уравнение δЭ=0 гарантирует выполнение уравнений равновесия и краевых условий, т.е. приводит к точному решению задачи.

Условию равновесия системы соответствует равенство нулю первой вариации полной энергии:

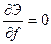
Исходя из этого определяем зависимость между продольным усилием и перемещением:

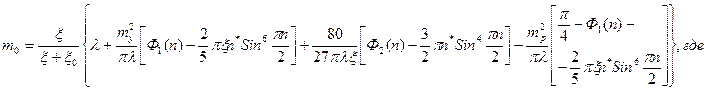
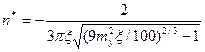
Длина волны выпучивания, соответствующая минимальному значению продольного усилия из условия:

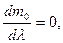
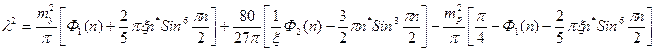
Строим диаграмму зависимости полного прогиба ξ+ξ₀ от продольного усилия m₀.

Следуя классификации (Я.Г.Пановко) имеет место потери устойчивости второго рода:

• неизменность конфигурации (не считая величины прогибов) системы в процессе ее постепенного нагружения;
• существование максимума нагрузки – критической силы второго рода;
• отсутствием разветвления форм устойчивого равновесия.

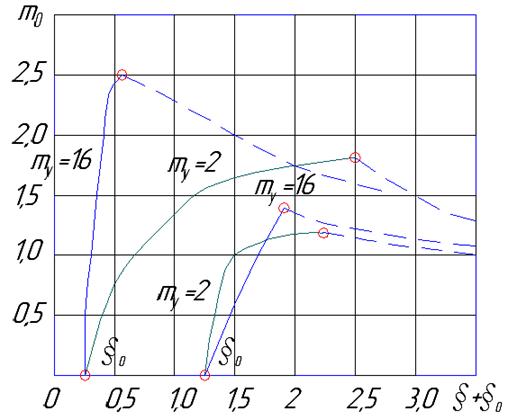
m_y – характеристика упругой работы грунта.

Левая часть кривой равновесных состояний (dm_o/dξ>0) является устойчивой.

Если исследовать полную энергию системы (Э), получаем:

• вторая вариация полной энергии положительна для левой части;
• для правой части 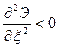отрицательна;
• точка соединения левой (сплошной) и правой (пунктирной) части диаграммы соответствует нулевой значение

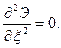
Значение m_кр соответствует экстремальному значению m₀, т.е. точке соединения левой и правой ветвей.

Зависимости параметра продольного усилия m_кр от упругой работы грунта m_y, при различных значениях ξ₀ и зоны разгрузки m_р.

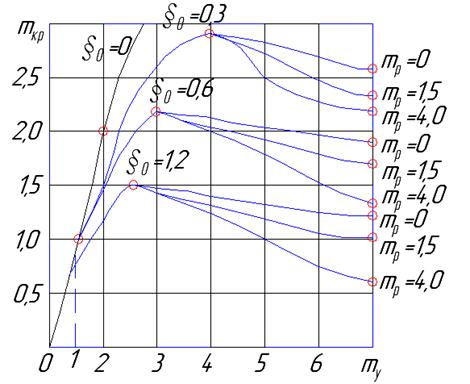
Большой интерес – анализ m_кр в соответствии с диаграммой.

1. При малых начальных значениях ξ₀ (стрела прогиба) параметр упругой работы грунта my имеет значительное влияние на m_кр (и соответственно на продольное критическое усилие).

2. При ξ₀=0, т.е. трубопровод не имеет упругого изгиба (прямолинейный), а также если на всем участке выпучивания грунт работает только в упругой области (n=1; n=a/l; a=l).

Критическая сила будет m_кр=m_y.

Это решение совпадает с решением для прямого стержня в упругой среде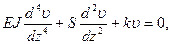

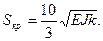
Кривая равновесных состояний имеет асимптоту m₀=m_кр и аналитическое выражение этой кривой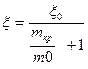

3. При больших значениях начального прогиба ξ₀ и параметра m_y влияние упругой зоны работы грунта на продольное критическое усилие незначительно, однако при этом сказывается влияние зоны разгрузки (m_р).

Если пренебречь влиянием упругой зоны и считать n=0, т.е.a=0. Можно получить решение в замкнутом виде:

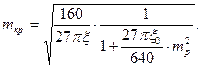
Минимальная длина волны и стрела выпучивания, соответствующие потере устойчивости.

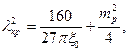где

λ – параметр длины выпученного участка.

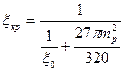
При определении и исследовании полной энергии системы усилие S₀ принять постоянным по длине и независимым от длины и стрелы волны выпучивания.

Величина S₀ представляет собой алгебраическую сумму:

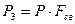– воздействие продукта на заглушку, где

F_св – площадь трубы в свету;

N₀ – продольное усилие, вызванное деформацией трубопровода под действием внутреннего давления и температуры.

Неизвестное условие N₀ определяет условия неразрывн. перемещений:

W₁+W₂=0 – фиктивные продольные перемещения нулевого сечения участка выпучивания (подчеркиваем аналогично с компенсатором) и примыкания прямолинейного участка.

Для участка выпучивания:

Деформация изогнутого элемента связана с перемещением нелинейной зависимостью:

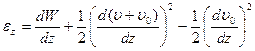
С другой стороны:

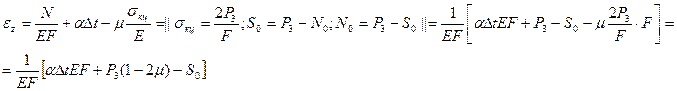Сравнивая выражения получаем:

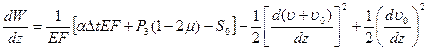
Производим интегрирование с учетом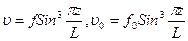

Получаем 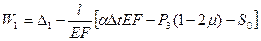, где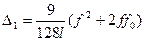

W₂ – определяется также как в предыдущей лекции.

Используя условие неразрывности W₁+W₂=0, получаем уравнения для определения продольного усилия в зависимости от нагрузки:

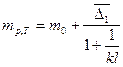– при отсутствии участка предельного равновесия грунта при продольном перемещении.

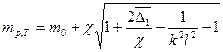– при наличии t_кр, где

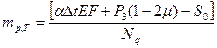– параметр нагрузки;

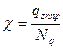– характеристика работы грунта участка предельного равновесия при продольном перемещении;

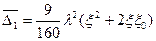– безразмерное удлинение участка выпучивания;

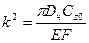– продольное перемещение.

Критерий отсутствия участка предельного равновесия грунта при продольных перемещениях:

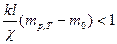
Важнейшая задача: допустимые давления в трубопроводе и Δt.

Проанализируем влияние начальной прочности ξ₀ и примыкающих к месту выпучивания прямолинейных участков на продольное усилие S₀ от P и Δt.

Полученные уравнения для m_p,т позволяют по известному значению критического продольного усилия m₀=m_кр определить критическую нагрузку m_p,т. В этом случае при определении Δ₁ значения волны выпучивания λ и стрелы прогиба ξ необходимо принимать равными λ_кр и ξ_кр. Так как λ_кр и ξ_кр зависят только от начальной стрелы прогиба ξ₀ и параметров грунта, то уравнения для m_p,т становятся линейными относительно m₀=m_кр.

Упрощенные зависимости для практических расчетов.

Для практических расчетов используют упрощенную зависимость, с допущениями, идущими в запас прочности.

1. Для прямолинейных участков заглубленного в грунт трубопровода критического продольного усилия:

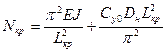
Расчетная длина волны выпучивания, соответствующая минимальному значению критического усилия:

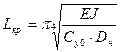
Подставляя L_кр, получаем min значение критического продольного усилия:

2. Для подземных участков трубопровода с углами поворота, обращенными выпуклостью вверх:

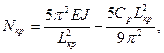
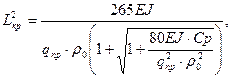где

ρ₀ – расчетный радиус оси изгиба трубопровода.

Исходя из расчетного радиуса оси изгиба min значения критического продольного усилия:

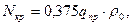где

q_пр – предельное сопротивление поперечному перемещению трубопровода вверх.

Дополнительная стрела прогиба, соответствующая потере устойчивости:

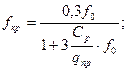
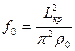(*), где

C_p – параметр разгрузки грунта.

3. Наземный трубопровод, уложенный в насыпи, с изгибом в горизонтальные плоскости.

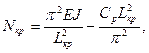
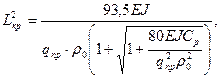
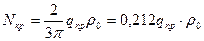
Стрела прогиба также *.

4. Эквивалентное продольное сжимающее усилие обусловлено изменением температуры, давления и зависит от деформативности системы.

Как показал приведенный анализ (см. выше) при малых начальных искревлениях перемещения системы незначительны и эквивалентное сжимающее усилие можно определить без учета деформативности системы.

При расчетном радиусе изгиба ρ₀≥1000D_н.

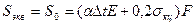
При меньшем расчетном радиусе (ρ₀≤1000D_н) S_экв вычисляется по формулам, учитывающие продольные связи и “Самокомпенсацию” системы:

• при отсутствии участка предельного равновесия грунта; при продольном перемещении, когда выполняется условие:

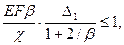
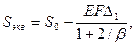
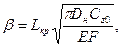
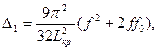
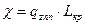
• условие не выполняется (наличие участка предельного равновесия грунта):

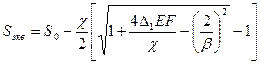
Начальный изгиб характеризуется ρ₀. В соответствии с принятой постановкой задачи под расчетным радиусом ρ₀ понимается или радиус изгиба оси трубы, если изгиб имеет место на всей длине волны выпучивания. Это наблюдается при свободном (упругом) изгибе трубопровода.

Таким образом, если длина хорды кривой больше или равна критической длине волны выпучивания, то в качестве расчетного род. Принимается фактический радиус оси изгиба трубы, т.е. при 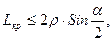ρ₀=ρ, где

ρ - min радиус оси изгиба трубы;

α – угол поворота оси трассы трубопровода.

Согласно СНиП 2.05.06-85.

Проверку общей устойчивости трубопровода в продольном направлении в плокости наименьшей жесткости системы следует производить из условия:

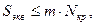где

m – коэффициент условий работы трубопровода.

Лекция 10.

Расчет компенсаторов.

Если уже определены и заданы расстояния между компенсатором их расчет сводится к выбору геометрических параметров из условия восприятия перемещения прямолинейной части МТ, обусловленного Δt и P.

Если компенсатор находится в месте выхода подземного МТ на поверхность, то перемещение, на котором должен рассчитываться компенсатор, складывается из перемещения открытого участка W₂ и перемещения в месте выхода из грунта W₁.

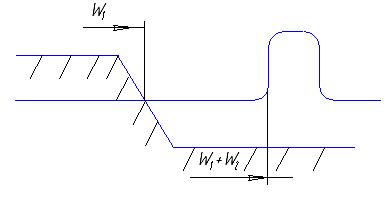
Если геометрические параметры компенсатора заданы, то рассчитывается предельное перемещение воспринимаемое этим компенсатором.

Расчет ведут по допускаемому уравнению продольных напряжений.

Для определения продольных напряжений вычисляют его податливость, т.е. перемещение его конца от единичной силы H⁰=1. Для общности решения рассмотрим трапецеидальный компенсатор.

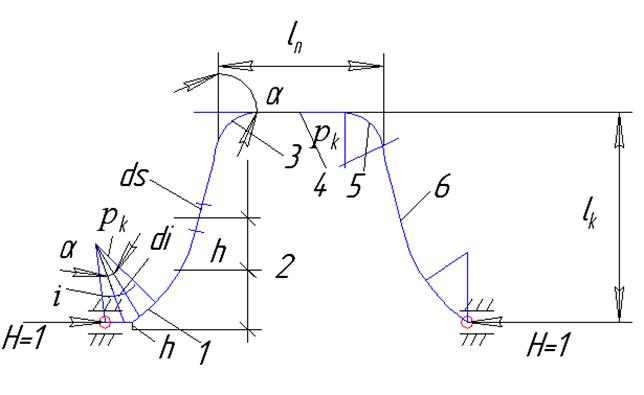
ρ_к – радиус оси изгиба отвода;

α – угол поворота;

l_к – вылет компенсатора;

l_п – длина полки.

Конструкция компенсатора представляет собой систему, состоящую из круговых отводов и прямолинейных участков.

Податливость определяется, как для стержневой системы 1, 3, 5, 7 – круговые участки радиусом ρ_к, 2,4,6 – прямолинейные.

δ₁₁ – податливость, перемещенная в направление силы Н=1, от этой же силы Н=1.

Для определения δ₁₁ используем известный из курса сопротивления материалов метод Мора (интеграл Мора):

где

L – длина стержневой системы;

δ₁ – перемещение от системы внешних сил, которое создает М_р (в расчет не берутся продольные силы).

Для случая, когда вместо системы внешних сил Н=1.

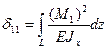(для случая EJ_x=const).

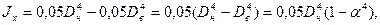
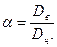
В силу симметрии компенсатора будем рассматривать 1, 2, 3 и половину 4 участка.

1 участок:

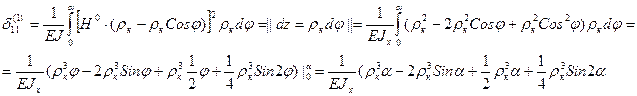2 участок:

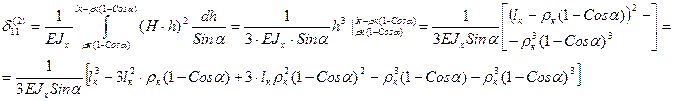
3 участок:

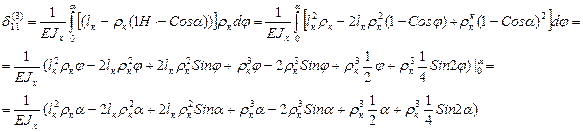
4 участок:

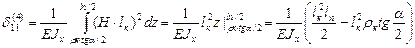
Полученные выражения нужно умножить на 2, чтобы получить полную податливость компенсатора. Кроме того, необходимо коэффициентом k_ж учесть уменьшение жесткости круговых частей компенсатора.

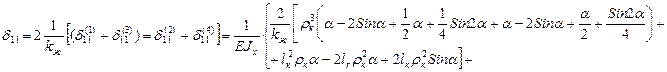
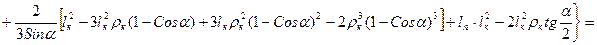
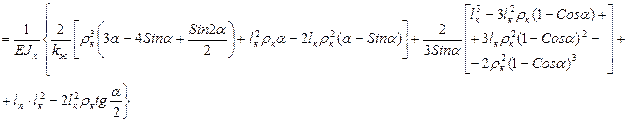Для того, чтобы определить податливость наиболее часто встречающихся П-образных компенсаторов необходимо принять α=π/2:

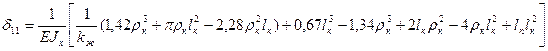
Для Z-образного компенсатора необходимо рассмотреть только первые три участка. Для α=π/2.

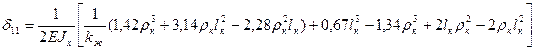
Податливость Г-образного компенсатора:

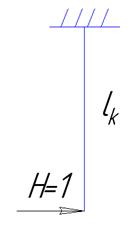
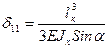
При α=π/2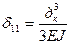

Формулы соответствия СНиП 2.05.06-85

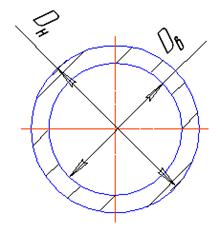
Необходимо отметить особенность, которая возникает в изогнутой части трубы. Здесь более сложное напряженной состояние. Это объясняется тем, что в процессе изгиба изменяется форма поперечного сечения.

В классической теории расчет кривых брусьев положена гипотеза неизменной формы поперечного сечения при изгибе. В данном же случае (расчет отводов при изгибе) форма поперечного сечения изменяется под действием возникающих сил.

Рассмотрим два сечения. На выпуклой стороне растягивающее напряжение, на вогнутой – сжимающее. Равнодействующие силы Т направлены к нейтральной оси и вызывают сплющивание поперечного сечения отвода при изгибе.

Для получения более точного решения вводят коэффициент понижения жесткости отводов при изгибе k_ж.

Для стальных отводов при μ=0,3, k_ж=λ/1,65, λ=δR/r², где

λ – коэффициент кривой трубы, геометрическая характеристика отвода;

R – радиус изгиба отвода;

r – средний радиус кольцевого сечения отвода.

Если в продольном напряжении перемещение Δк (в месте примыкания трубопровода к компенсатору в напр. Н).

Н_к=Δк/δ₁₁ (Н_к во столько раз больше Н=1, во сколько Δ_к больше δ₁₁)

Зная распор компенсатора максимальный изгибающий момент в сечении, наиболее удален от действительной силы Н_к.

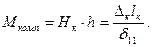
Максимальное продольное напряжение, возникающее в отводе компенсатора необходимо вычислять с учетом коэффициента увеличения m_к=0,9/λ_к^2/3

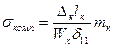
Надземный трубопровод:

• разрезная расчетная схема;
• неразрезная,

Разбивка опор при смещении в плане оси трассы трубопровода.

Ригель – линейный несущий элемент (сплошной или решетчатый) в конструкциях зданий и сооружений. Соединяет стойки, колонны (ригельные рамы); служит опорой плит (ригельные перекрытия, покрытия). Выполняется из ж-б, стали, дерева.

Расчет опор и эстакад магистральных и технологических трубопроводов.

Прокладка трубопровода может осуществляться:

• по опорам;

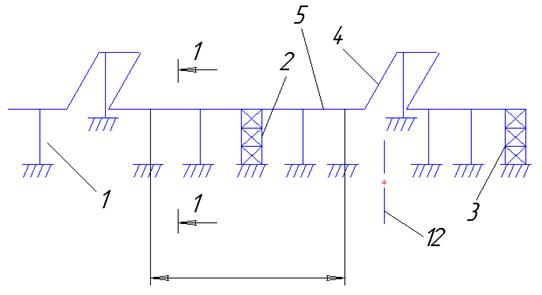
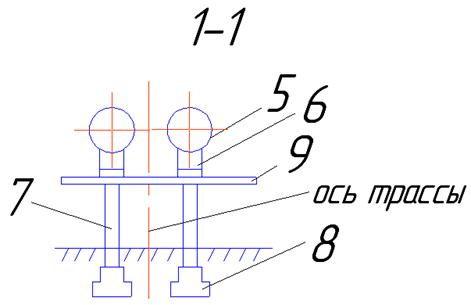
• по эстакадам.

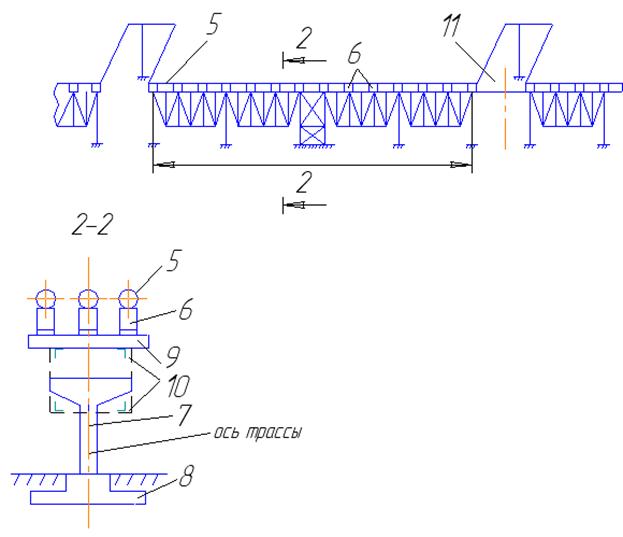
1 – промежуточная опора;

2 – анкерная промежуточная опора;

3 – анкерная концевая опора;

4 – компрессор;

5 – трубопровод;

6 – опорная часть трубопровода;

7 – колонна;

8 – фундамент;

9 – траверса;

10 – пролетное строение;

11 – вставка температурного блока;

12 – ось температурного разрыва.

Разрезная расчетная схема – отдельные части которой соединены между собой компенсаторами.

Отдельно стоящая опора под трубопроводы состоит из одной или нескольких колонн, связей, траверсы и фундамента.

Эстакада состоит из опор (колонны, связи, ригели, фундаменты), пролетных строений (ферм, балок), траверс, связей по фермам.

В продольном направлении отдельно стоящие опоры и эстакады разбивают на температурные блоки, длина которых принимается в зависимости от предельного расстояния между неподвижными опорными частями трубопровода и расчета конструкции на климатические воздействия.

Температурный блок состоит из пролетных строений, одной анкерной опоры и промежуточных опор.

Анкерные промежуточные опоры устанавливают, как правило, в середине температурного блока.

В местах поворота или конца трассы применяются анкерные угловые или концевые опоры.

Передача нагрузок на отдельно стоящие опоры и эстакады от трубопровода производится посредством подвижных и неподвижных опорных частей трубопровода.

Восприятие температурного удлинения трубопровода осуществляется компенсаторами.

В зависимости от конструктивных решений, опоры и эстакады различают по следующим признакам:

• по материалу конструкций: железобетонные, стальные, комбинированные;
• по конструктивным решениям несущей конструкции пролетных строений, опор, фундамента;
• по высоте верха опор: низкие и высокие;
• по способу расположения труб на опорах и эстакадах: одноярусные, двухъярусные, многоярусные.

Прокладку трубопровода на эстакадах применяют при большом количестве трубопроводов малых диаметров.

Для уменьшения нагрузки на опоры и промежуточные строения эстакад используют самонесущую способность трубопровода большого диаметра с опиранием их только на траверсы над опорами эстакад.

В частности для МТ (СНиП 2.05.06 «Магистральные трубопроводы»)

“…7.3. При прокладке трубопровода и их переходов через естественные и искусственные препятствия следует использовать несущую способность самого трубопровода …”

При прокладки трубопровода по отдельно стоящим опорам на анкерных опорах предусматривается неподвижное крепление трубопровода.

Расстояние между отдельно стоящими опорами под трубопровод назначаются исходя из расчета труб на прочность и жесткость.

Отдельно стоящие опоры и эстакады рекомендуют, как правило, проектировать сборными из железобетонных конструкций с ненапряженной или напряженной арматурой.

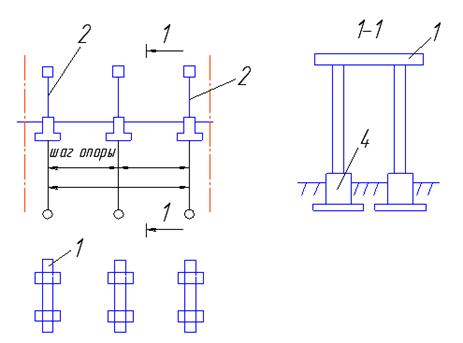
1 – железобетонные траверсы;

2 – промежуточная железобетонная опора;

3 – анкерная промежуточная железобетонная опора;

4 – фундамент.

Дата добавления: 2014-01-07