Основные задачи, решаемые при проектировании

На каждом уровне блочно-иерархического проектирования исходными данными являются данные ТЗ, а результатом – техническая документация.

Проектирование сводится к решению определенных задач, относящихся либо к задачам синтеза, либо к задачам анализа.

Понятие «синтез» технического объекта в широком смысле слова близко по содержанию к понятию «проектирование». Разница заклю­чается в том, что проектирование означает весь процесс разработки объекта, а синтез характеризует часть этого процесса, когда создается какой-то вариант, не обязательно окончательный, т. е. синтез как задача может выполняться при проектировании много раз, перемежаясь с решением задач анализа.

Анализ технических объектов — это изучение их свойств; при анализе не создаются новые объекты, а исследуются заданные.

Синтез технических объектов нацелен на созда­ние новых вариантов, а анализ используется для оценки этих вариан­тов, т. е. синтез и анализ выступают в процессе проектирования в диа­лектическом единстве.

Для дискретных объектов задача синтеза является задачей опре­деления структуры.

Для непрерывных объектов решение задачи синтеза должно при­водить к определению структуры и численных значений внутренних параметров разрабатываемых устройств. Часто желательно различать задачи определения структуры и определения значений внутренних параметров — в дальнейшем будем использовать для этих задач со­ответственно термины «синтез структуры» и «расчет внутренних па­раметров» (структурный синтез, параметрический синтез). Если среди вариантов структуры ищется не лю­бой приемлемый вариант, а наилучший в некотором смысле, то такую задачу синтеза называют структурной оптимизацией. Расчет внутренних параметров, оптимальных с позиций некоторого критерия при заданной структуре объекта, называют парамет­рической оптимизацией. Как будет показано ниже, воз­можности постановки и решения задач структурной оптимизации су­щественно ограничены, поэтому обычно под оптимизацией понимают только параметрическую оптимизацию. Таким образом, параметри­ческая оптимизация — это определение таких значений внутренних параметров X, при которых некоторая функция F(X), называемая целевой функцией или функцией качества, при­нимает экстремальное значение.

К определяемым при оптимизации внутренним параметрам может относиться только часть параметров элементов, называемых управ­ляемыми параметрами. Если использовать геометриче­ские представления при описании процедур оптимизации, то можно говорить о n-мерном пространстве, осями координат которого являются оси управляемых параметров. Это пространство называют про­странством управляемых параметров. Каждой точке этого пространства соответствует определенная совокупность значений параметров х_l — определенное значение вектора управляе­мых параметров X= (х1, х2,..., х_п). Точку, соответствующую выб­ранному на данном этапе проектирования значению X, называют отображающей точкой. Аналогично можно использовать понятие пространства выходных параметров.

Задача анализа объекта сводится к получению некоторой информа­ции о свойствах объекта в заданной отображающей точке или в доста­точно малых окрестностях этой точки. Различают несколько видов задач анализа. По частоте применения задачи анализа делят на типовые и нетипо­вые. Первые встречаются при проектировании разнообразных объ­ектов, их решение дает информацию об основных свойствах объектов. Нетиповые задачи анализа служат для получения некоторой допол­нительной информации, причем алгоритмы решения этих задач могут быть разнообразными и заранее не известными.

Другой принцип классификации задач анализа приводит к их де­лению на группы задач одновариантного и многовариантного анализа. Решение задач одновариантного анализа позволяет получить информацию о выходных параметрах объекта непосредствен­но в заданной отображающей точке, причем чаще всего решение сводится к однократному решению системы уравнений или к однократ­ному испытанию макета объекта.

Типовыми задачами одновариантного анализа являются:

- анализ статического состояния;

- анализ переходного процесса;

- анализ частотных характеристик;

- анализ устойчивости;

- анализ стационарных режимов колебаний.

Многовариантный анализ заключается в исследо­вании поведения объекта в некоторой окрестности заданной отобра­жающей точки. Обычно многовариантный анализ требует много­кратного выполнения одновариантного анализа. К типовым задачам многовариантного анализа относят прежде всего:

- статистический анализ;

- анализ чувствительности.

Если решение задач одновариантного анализа дает ответ на вопрос, выполняются ли условия работоспособности в заданном варианте структуры при номинальных значениях внут­ренних параметров, то решение задачи статистического анализа от­вечает также на вопрос, с какой вероятностью будут выполняться ус­ловия работоспособности. Действительно, внутренние параметры любого технического объекта не могут быть выдержаны с любой же­лаемой точностью. Вследствие неизбежных погрешностей технологи­ческого оборудования, разброса параметров исходных материалов параметры элементов оказываются случайными величинами. Так как выходные параметры суть функции параметров элементов, то они также являются случайными величинами. По­этому при серийном производстве изделий каждый экземпляр будет иметь свои случайные значения выходных и внутренних параметров, причем у части экземпляров условия работоспособности могут вы­полняться, а у другой части — не выполняться. Знание вероятности выполнения условий работоспособности имеет важное значение в процессе проектирования, так как эта вероятность характеризует такие свойства проектируемого объекта, как надеж-ность и серийнопригодность.

Анализ чувствительности позволяет определить степень влияния внутренних и внешних параметров объекта на выходные параметры. Поэтому данный вид анализа широко используется для оценки не­стабильности выходных параметров при воздействии внешних деста­билизирующих факторов. Другое важное назначение анализа чувствительности заключается в получении информации о том, в каком направлении и какие управляемые параметры следует изменять в процессе оптимизации. Действительно, чтобы улучшить свойства объекта, надо экстремизировать целевую функцию, поэтому необ­ходимо изменять те управляемые параметры, которые существенно влияют на целевую функцию.

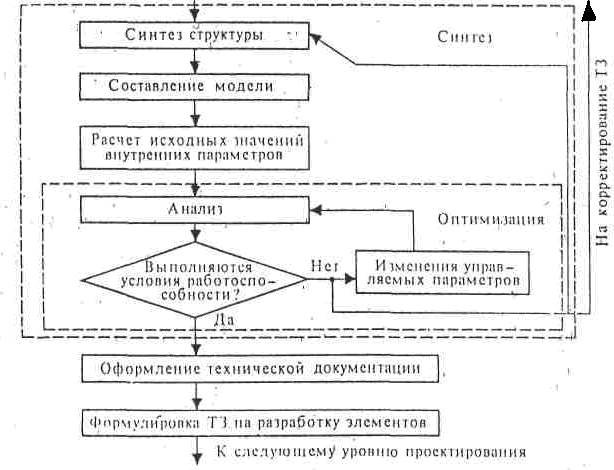
Схема процесса проектирования на очередном иерархическом уровне.

Схема процесса проектирования на каждом уровне проек­тирования представляется как решение совокупности задач; этот процесс иллюстрируется схемой. Разработка блока по предъявленному ТЗ начинается с синтеза структуры. Исходный вариант структуры генерируется, а затем оценивается с позиций удовлетворе­ния условий работоспособности. Для каждого варианта структуры предусматривается оптимизация параметров, поскольку оценка долж­на выполняться при оптимальных или близких к оптимальным зна­чениях внутренних параметров. В свою очередь, оптимизация осу­ществляется путем многократного анализа. Если для некоторого варианта структуры достигнуто выполнение условий работоспособ­ности с заранее оговоренным запасом, то задача синтеза считается решенной; результаты проектирования блока оформляются в виде необходимой технической документации и ТЗ на разработку элемен­тов блока.

Для каждого варианта структуры составляется модель объекта. Эта модель может быть математической при машинном проектировании или физической при экспериментальной отработке изделия. Модель должна быть адекватной объекту в отношении ос­новных интересующих разработчика свойств. Численные значения параметров элементов модели устанавливаются либо на основе про­стых ручных расчетов, либо берутся сугубо ориентировочными на основе опыта и интуиции инженера. Далее анализом модели, провер­кой выполнения условий работоспособности и принятием решения по результатам проверки производится параметрическая оптимизация, Если условия работоспособности в процессе оптимизации не выпол­няются, то изменяются параметры элементов и модель анализируется при этих значениях параметров. При успешном решении задачи опти­мизации переходят к завершающим процедурам, в противном слу­чае — к генерации нового варианта структуры. Если перебор многих вариантов структуры не приводит к успеху, то ставится вопрос о пере­смотре ТЗ на разработку блока, т. е. происходит возврат к преды­дущему уровню блочно-иерархического проектирования.

Схема отражает типичную последовательность процедур при проектировании, однако в конкретных ситуациях могут быть естественные отклонения от этой последовательности. Так, при раз­работке дискретных объектов оценка каждого варианта обычно осу­ществляется более простыми средствами, чем решением сложной задачи параметрической оптимизации; в некоторых случаях структу­ра блока может быть заданной или известной из некоторых источников (тогда из схемы исключают процедуру синтеза струк­туры).

В связи с итерационным характером процесса проектирования процедуры по схеме могут выполняться многократно. Обычно на первых итерациях блок анализируется менее тщательно, например проверка выполнения условий работоспособности может проводиться только в номинальном режиме. На последних итерациях становится оправданным трудоемкий статистический анализ.

Задача параметрической оптимизации также может быть заменена более простой задачей расчета внутренних параметров, если до дости­жения экстремума получается приемлемая степень выполнения усло­вий работоспособности.

Особенности немашинных и машинных методов проектирования. При проектировании должны выбираться методы и средства решения проектных задач, которые обеспечивают наилучшее достижение цели. Последнее может пониматься в смысле минимальности сроков проек­тирования, минимальности материальных затрат, оптимальности полу чаемых проектных решений.

В своей проектной деятельности инженеры используют в разум­ном сочетании экспериментальные, расчетные и интуитивно-эвристи­ческие методы проектирования. Интуиция и опыт инженера необхо­димы прежде всего при решении задач синтеза структуры большинст­ва технических объектов. Для решения задачи определения значений внутренних параметров используют расчетные и экспериментальные методы.

Расчетные ручные методы проектирования могут дать только сугубо ориентировочные значения параметров, которые следует рас­сматривать как исходные, требующие корректировки с помощью дру­гих методов. Ориентировочный характер результатов ручных расче­тов связан с малой точностью ручных расчетных методик. Действи­тельно, процессы в достаточно сложных технических объектах опи­сываются системами уравнений высокого порядка; эти уравнения в общем случае нелинейны. Так, переходные процессы в электронных схемах описываются системами, обыкновенных дифференциальных уравнений, порядок которых равен приблизительно количеству ре­активных элементов. Для схем средней степени интеграции типичные порядки систем уравнений оказываются равными 50 — 500. Анали­тическое решение системы обыкновенных дифференциальных урав­нений удается получить практически только в случае, если порядок системы не превышает двух и уравнения линейны. Этот пример по­казывает, что ручные расчетные методы применимы только при при­нятии существенных упрощений, что и обусловливает ориентировоч­ный характер получаемых результатов. Следовательно, анализ рабо­тоспособности выбранного варианта уже не может быть выполнен ручными расчетными методами. Поэтому в рамках традиционного подхода (без использования ЭВМ) неизбежным было применение экспериментальных методов, т. е. методов макетирования. Именно на макете — физической модели — определялось выполнение усло­вий работоспособности, производилось изменение внутренних пара­метров, частичное изменение структуры с целью улучшения свойств объекта. Конечно, на макете, как правило, допустимы не любые изменения, так как цена ряда изменений слишком велика. Во многих случаях экспериментирование невозможно на достаточно высоких иерархических уровнях — здесь стоимость изготовления макета есть стоимость изготовления опытного образца и согласиться на много­кратное изготовление образцов в итерационном процессе проекти­рования сложных систем нельзя. Поэтому при традиционном под­ходе задачи оптимизации практически не решались — разработчик удовлетворялся получением первого работоспособного варианта.

Машинные методы появились прежде всего как результат стремления заменить дорогостоящее и длительное физическое моде­лирование математическим моделированием. В этих методах вместо макета используют математическую модель проектируемого техниче­ского объекта.

Математическая модель — это совокупность мате­матических объектов (чисел, переменных, векторов, множеств и т. п.) и отношений между ними, которая адекватно отображает некоторые свойства проектируемого технического объекта. Например, большой и важный класс математических моделей составляет системы урав­нений. В процессе проектирования применяют те математические модели, которые отображают существенные с позиций инженера-проектировщика свойства объекта.

Отсутствие требования существенных упрощений может привести к точности математической модели, вполне достаточной для решения задач проектирования. Во многих случаях точность математической, модели оказывается не ниже точности, обеспечиваемой при физиче­ском моделировании. Наличие быстродействующей ЭВМ с достаточ­ной емкостью оперативной памяти обусловливает возможность ис­следования математической модели в приемлемое время. В то же вре­мя для математической модели характерна легкость изменения лю­бых параметров, что позволяет выполнять анализ более всесторонний и исчерпывающий.

Таким образом, в схеме процесса проектирования с появлением машинных методов изменилось содержание большинства процедур. Прежде всего, в процедуре «составление модели» физи­ческое моделирование сменилось математическим и процедура «ана­лиз» превратилась в исследование математической модели — решение системы уравнений. Дальнейший шаг был сделан в направлении алгоритмизации процедуры «изменение управляемых параметров». Изменения параметров удалось сделать целенаправленными, под­чиненными стратегии поиска экстремальных значений некоторой целевой функции, вычисляемой в процедуре «анализ». Таким обра­зом, на ЭВМ оказалась реализованной задача параметрической опти­мизации.

Другой важной задачей, широко решаемой на ЭВМ, явилась за­дача оформления технической документации. Решение этой задачи связано с развитием машинной графики.

Формулировка задач моделирования и анализа при применении машинных методов проектирования. Выше было введено понятие вы­ходных, внутренних и внешних параметров объектов проектирова­ния. Математические модели, в которых фигурируют только эти параметры, обычно являются аналитическими моделями. Однако получение подобных аналитиче­ских моделей — явление довольно редкое в практике проектирования. В общем случае уравнения математической модели связывают физические величины, которые характеризуют состояние объекта и не относятся к перечисленным выше выходным, внутренним или внешним параметрам (например, скорости и силы в механических).

Дата добавления: 2014-01-07