Одномерная оптимизация. Прямой метод

Классификация методов оптимизации

По виду искомого экстремума поисковые методы оптимизации могут быть классифицированы следующим образом:

1. Методы безусловной оптимизации

предназначены для нахождения минимума или максимума функций, на переменные которых не накладываются никакие ограничения

2. Методы условной оптимизации

предназначены для решения оптимизационных задач с ограничениями, накладываемыми либо на сами переменные, либо на их связи

3. Методы локальной оптимизации

отыскивающие локальные минимальные или максимальные значения целевой функции (практически все методы оптимизации относятся к локальным)

4 Методы глобальной оптимизации

это те методы и практические приемы, которые позволяют отыскивать глобальный оптимум (наилучшую среди локальных оптимальных точек)

При решении оптимизационных задач большое значение имеют методы безусловной оптимизации, поскольку часто задачи условной оптимизации (задачи с ограничениями) сводятся различными способами к задачам безусловной оптимизации.

Классификация этих методов может быть представлена в виде схемы

Локальные методы безусловной оптимизации:

1. Нулевого порядка f(x)

- методы одномерного поиска - методы многомерного поиска

- метод золотого сечения - методы покоординатного спуска

- метод дихотомии - метод деформируемого многогранника

- метод квадратичной интерполяции - метод случайного поиска

2. Первого порядка f(x), f’(x)

- метод наискорейшего спуска

- метод сопряженных градиентов

- метод проекции градиента

3. Второго порядка f(x), f’(x), f’”(x)

- метод Ньютона

- метод Пауэлла

Методы нулевого порядка в качестве исходной информации используют лишь значения целевой функции (нулевая производная). Реализация методов первого порядка требует знания первых производных, входящих в модель функций. При использовании методов второго порядка необходимо вычислять, кроме значений целевой функции и ограничений, еще и значения первых и вторых производных всех функций, входящих в модель.

Эффективность методов обычно возрастает с ростом порядка метода.

Метод одномерного поиска, т.е. функций одной переменной, делится на прямой и итерационный.

Рассмотрим прямой (аналитический) метод.

В отношении функций, для которых находится экстремум, минимальное предложение для применения аналитических методов состоит в следующем: для f(x) в промежутке (а,в), где отыскивается экстремум, существует конечная производная f’(x).

Вспомним необходимые и достаточные условия существования экстремума f(x) на промежутке (а,в).

Необходимое условие:

Если в точке Хо функция имеет экстремум, то f’(Xo)=0. Точка Хо при выполнении необходимого условия называется стационарной точкой.

Достаточное условие:

1. Устанавливаем знак f’(x) для Хо<Х и Хо>Х.

Если при увеличении Х производная меняет знак «+» на знак «-», то имеет место максимум.

Если же меняется с «-«на «+», то имеем минимум.

Если знак не меняется – экстремума нет.

2. Вычисляем вторую производную в точке Хо.

Если f”(x)>0, то f(x) имеет минимум.

Если f”(x)<0, то f(x) имеет максимум.

В различных заданиях оптимизации требуется отыскивать либо минимум, либо максимум целевой функции. Покажем, что с математической точки зрения задача максимизации критерия эффективности идентична задача минимизации

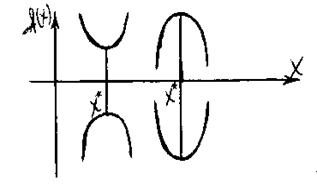
Чаще ищут min f(x), но это равносильно отысканию max [-f(x)], то есть max[f(x)] = min[-f(x)]. Это утверждение достаточно убедительно иллюстрирует рисунок:

 

Дата добавления: 2014-01-07