Метод тяжелого шарика

Логической основой метода тяжелого шарика является физическое уравнение движения материальной точки в силовом поле. Пусть х- скалярная координата, f(х)-потенциал поля, 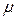-множитель, пропорциональный массе точки, q- множитель, связывающий потенциал поля и силу, р- коэффициент трения среды. Тогда уравнение движения точки будет выглядеть следующим образом:

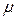
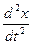=-q(grad(f(x)))-p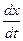

Здесь grad f (x) является горизонтальной проекцией действующей силы.

Запишем это дифференциальное уравнение в виде разностного, учитывая, что слева будет вторая разность:

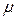∆x(k)=-q(grad f (x(k)))-p∆x(k).

Учитывая далее, что ∆x(k)=∆x(k)-∆x(k-1) и ∆x(k)=x(k+1)-x(k), после алгебраических преобразований и переобозначения констант, получаем:

x(k+1)=x(k)-α(grad f (x(k)))+β(x(k)-x(k-1)).

Мы получили некоторое уравнение перемещения точки в направлении уменьшения функции. Это и есть уравнение метода тяжелого шарика. По сравнению с методами первого порядка оно обладает тем преимуществом, что, по существу, использует вторую производную, то есть имеется больше информации о профиле функции. Одновременно здесь отсутствует главный недостаток методов второго порядка - необходимость оценки второй производной. Этот метод достаточно эффективен при поиске минимума овражных функций.

Раздел 3. Нелинейное программирование.

Дата добавления: 2014-01-07