
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод Лагранжа
|
|
|
|
Рассмотрим классический метод множителей Лагранжа. Классическая задача Лагранжа есть задача с ограничениями-равенствами, мы же проследим ее логическое развитие для задачи с ограничениями-неравенствами.
Итак, пусть ограничения заданы только равенствами h(x)=0. Как известно из математического анализа, для решения такой задачи на условный минимум записывается функция Лагранжа:
L(x, λ) = f(x) – λTh(x),
где λ - вектор множителей Лагранжа.
Условия минимума записываются в следующем виде:
а) условия первого порядка:
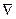 xL(x, λ) =
xL(x, λ) = 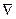 x f(x) – λT
x f(x) – λT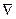 xh(x) = 0 (минимум по x);
xh(x) = 0 (минимум по x);
(1) 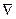 λ L(x, λ) = h(x) = 0 (максимум по λ).
λ L(x, λ) = h(x) = 0 (максимум по λ).
б) условия второго порядка:
yT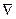 2xx L(x, λ) y > 0 для всех векторов y, не равных нулю и удовлетворяющих условию:
2xx L(x, λ) y > 0 для всех векторов y, не равных нулю и удовлетворяющих условию: 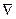 xht(x)y = 0.
xht(x)y = 0.
Здесь 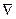 2xx L(x, λ) обозначена матрица вторых производных (матрица Гессе), которую для удобства в дальнейшем будем обозначать H (x, λ).
2xx L(x, λ) обозначена матрица вторых производных (матрица Гессе), которую для удобства в дальнейшем будем обозначать H (x, λ).
Для решения этой задачи можно применить один из двух способов:
- непосредственный поиск седловой точки функции L (x, λ)
одним из известных алгоритмов численного поиска безусловного
экстремума;
- решение (скорее, также численное) системы уравнений (1) -
условий минимума первого порядка.
Пусть теперь в исходной формулировке присутствуют ограничения-неравенства gj(x)>=0. Тогда для решения задачи используем следующий характерный прием. Превратим неравенства в эквивалентные равенства путем введения фиктивных переменных zj:
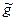 j (x,z)=gj(x) – zj2=0
j (x,z)=gj(x) – zj2=0
Как видно из этого выражения, для какой-либо фиксированной точки x существует значение zj, для которого это равенство справедливо.
Таким образом, введение фиктивного вектора z размерности r позволяет свести исходную задачу с неравенствами к новой искусственной задаче с равенствами. В этой задаче функция Лагранжа имеет вид:
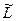 (x, z, λ, μ) = f(x) – λTh(x) – μT
(x, z, λ, μ) = f(x) – λTh(x) – μT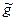 (x, z)
(x, z)
где - μ вектор множителей при искусственных равенствах, имеющий тот же смысл, что и вектор λ.
Поскольку функция 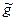 j(x, zj) явно выражена через zj, то фиктивные переменные теперь можно исключить, записав условия минимума первого порядка.
j(x, zj) явно выражена через zj, то фиктивные переменные теперь можно исключить, записав условия минимума первого порядка.
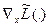 = x f(x) – λT x(x) – μT
= x f(x) – λT x(x) – μT 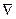 x
x 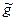 (x, z) = 0;
(x, z) = 0;
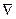 x
x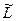 (.) = – μ z
(.) = – μ z 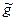 (x, z) = 2μT z = 0;
(x, z) = 2μT z = 0;
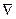 x
x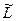 (.) = - h(x) = 0;
(.) = - h(x) = 0;
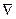 x
x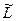 (.) = - g(x, z) = 0;
(.) = - g(x, z) = 0;
где (.) – (x, z, λ, μ).
Учитывая соотношения 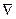 x g(x, z) =
x g(x, z) =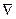 x
x 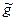 (x) и zj =
(x) и zj =  , а также то, что равенствам
, а также то, что равенствам 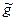 (x, z) = 0 соответствуют неравенства g(x)>=0, перепишем эту систему уравнений в виде:
(x, z) = 0 соответствуют неравенства g(x)>=0, перепишем эту систему уравнений в виде:
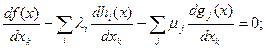
μj gj(x) = 0; i = 1, m; j = 1, r; k = 1, n;
hi(x) = 0;
gj(x) >= 0;
μj >= 0.
Эта система уравнений и неравенств называется условиями Куна - Таккера. Последняя группа неравенств (неотрицательность компонент вектора μ) следует из условий минимума второго порядка.
Отметим, что равенства μj = 0 имеют место для пассивных неравенств (действительно, их можно исключить из функции Лагранжа). Напротив, для активных неравенств μj строго положительны.
Различают отдельные классы задач нелинейного программирования. Среди них обычно выделяют так называемые задачи выпуклого программирования. Чтобы отнести задачу к этому классу, нужно иметь выпуклую функцию f(x), вогнутые функции gj(x) и линейные функции hi(x). Будем называть точку, удовлетворяющую условиям Куна - Таккера, точкой Куна - Таккера.
Отметим, что для задачи выпуклого программирования условия Куна - Таккера являются необходимыми и достаточными условиями минимума. При этом точка Куна — Таккера является единственной.
В задаче невыпуклого программирования обычно имеется несколько точек Куна - Таккера. Определить, какая из них является условным минимумом, можно только после выполнения условий второго порядка.
Другим выделяемым классом являются задачи квадратичного программирования. Они характерны тем, что f(x) - квадратичная форма, а все ограничения описаны линейными функциями. При этом условия Куна - Таккера являются системой линейных уравнений.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1027; Нарушение авторских прав?; Мы поможем в написании вашей работы!