Нелинейное преобразования случайных процессов

Рассмотрим теперь задачу о прохождении случайного процесса через нелинейную систему. В общем случае эта за­дача весьма сложная, но она значительно упрощается, ког­да нелинейная система является безынерционной. В безынер­ционных нелинейных системах значения выходного процесса 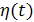в данный момент времени определяются значениями входного процесса 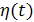в тот же самый момент времени. Для нелинейных безынерционных преобразований более простой задачей является определение функций распределения на вы­ходе и гораздо более сложной - определение корреляционной функции или энергетического спектра.

Как отмечалось выше, n - мерная функция распределе ния случайного процесса по сути дела является функцией рас­пределения n случайных величин, представляющих собой значения случайного процесса в n различных моментов вре­мени. Определение законов распределения функционально пре­образованных случайных величин является сравнительно простой задачей.

Рассмотрим простейший пример одномерной случайной величины. Пусть 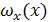плотность вероятности случайной величины x, которая подвергается нелинейному преобразованию 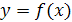. Определим плотность вероятности 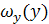случайной величины h. Предположим, что функция 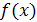такова, что обратная ей функция 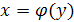- однозначна.

Если случайная величина x находится в достаточно малом интервале (х₀, x₀+ dx), то вследствие однозначной

функциональной зависимости между x и h случайная величина h обязательно будет находиться в интервале

(y ₀, y₀+ dy), где y₀=f(x₀); вероятности этих собы­тий должны быть одинаковыми, т.е.

(2.13)

откуда находим

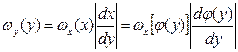(2.14)

Производная в последнем выражении берется по абсолютной величине, так как плотность вероятности не может быть отри­цательной. Если обратная функция j(y) неоднозначная, т.е. имеет несколько ветвей x_i=j_i(y), то для плотности вероят­ности с использованием теоремы сложения вероятностей мож­но получить

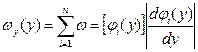(2.15)

Отметим, что для определения числовых характеристик нелинейно-преобразованных случайных процессов нет необхoдимости определять ихплотности вероятностей. Действительно, в общем случае для начального момента Н -го порядка имеем

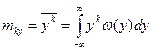(2.16)

Но согласно (3.4.13) 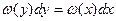и 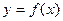.Поэто­му последнее выражение можно переписать

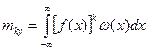(2.17)

Полученные выражения (2.14) и (2.15) легко рас­пространить на случай нескольких величин. Приведем здесь лишь окончательный результат для двумерного случая. Если случайные величины x_z и x₂ имеют совместную плотность вероятностей w_x(x₁, x₂), то для случайных величин

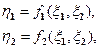(2.18)

при однозначности обратных функций

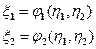
Совместная плотность вероятностей бцдет определятся выражением

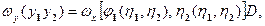(2.19)

Где величины

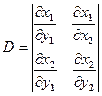(2.20)

называется якобианом преобразования и представляет собой от­ношение элементарных площадей ds/dS при переходе от одной системы координат к другой. Если D≠О, то справедливо равенство

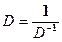(2.21)

Где

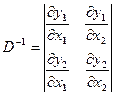
Дата добавления: 2014-01-07