
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Предварительный этап
|
|
|
|
Идея метода состоит из предварительного этапа и итераций. Их количество не больше n-2. Каждая итерация включает три этапа, начинаем первым этапом, заканчиваем вторым. Могут несколько раз повторяться первый и третий этапы. Каждая итерация связана с эквивалентным преобразованием матрицы C, полученной в результате предыдущей итерации и выбором максимального числа независимых нулей. Если число независимых нулей станет равным n то найдено оптимальное распределение.
Алгоритм венгерского метода для задачи назначения.

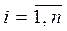
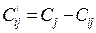
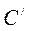 Шаг первый: В матрице C в каждом столбце находится максимальный элемент. Строится матрица элементы которой равны:
Шаг первый: В матрице C в каждом столбце находится максимальный элемент. Строится матрица элементы которой равны:

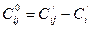
 Шаг второй: В матрице в каждой строке ищется минимальный элемент Строится матрица
Шаг второй: В матрице в каждой строке ищется минимальный элемент Строится матрица 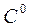 элементы которой будут равны.
элементы которой будут равны.
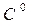
Шаг третий: В матриц выделяются независимые. Для этого последовательно просматриваются столбцы. В первом столбце любой 0 объявляется независимым и помечается знаком “ * ”, а столбец помечается знаком “ + ”. Далее просматриваются 0 второго столбца.Если во втором столбце найдется 0 который находится в строке где нет этого то он объявляется независимым и также помечается ” * ” и столбец помечается “ +” и т. д. Если в матрице выделено n независимых 0 т.е. все столбцы помечены знаком «+» то получено оптимальное решение. Этому решению соответствует позиция независимых 0 матрицы. Переходим на первый этап итерации.
Предположим, проведено k итераций. Приступаем к k+1 итерации.
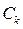 Этап первый.
Этап первый.
Шаг первый: Просматриваются невыделенные столбцы матрицы. Если в этих столбцах отсутствуют 0 то переход к этапу три.Если найден 0 то его отмечают знаком штрих, а строчку помечают знаком "+". Переходим на шаг второй.
Шаг второй: В отмеченной строке осуществляется поиск независимого 0 если он отсутствует, то переход к этапу второму. Если такой 0 есть, то аннулируется знак "+ " над столбцом в котором этот независимый 0 расположен.
Шаг третий: В этом столбце осуществляется поиск невыделенного 0, т.е. он должен находиться в строке, не помеченной знаком "+". Если такого 0 нет, то переход к этапу третьему. Если такой 0 есть, то он помечается знаком штрих, а строка помечается знаком "+". Затем просматривается эта строка. И отыскивается, если он есть независимый 0. Если есть, то аннулируется знак "+" над столбцом и т.д.За конечное число шагов процесс поиска заканчивается одним из двух исходов:
1) В строке, где есть 0 со штрихом нет независимых 0 - в этом случае переходим ко второму этапу.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 405; Нарушение авторских прав?; Мы поможем в написании вашей работы!