На орбиту без учета сопротивления атмосферы

Вывод искусственного спутника Земли (ИСЗ)

Третий закон Кеплера.

Второй закон Кеплера.

Первый закон Кеплера.

Орбита каждой планеты лежит в неподвижной плоскости, проходящей через центр Солнца и является эллипсом в одном из фокусов, которого находится Солнце.

Радиус вектор, соединяющий центры Солнца и планеты, ометает равные площади в равные промежутки времени ΔS₁=ΔS₂; Δt₁=Δt₂.

Квадраты времени обращения планет пропорциональны кубам их средних расстояний от Солнца.

Орбита, на которую выводится ИСЗ с течением времени изменяется, это связано с тем, что на спутник действуют:

§ хотя и небольшие, но в течении длительного времени аэродинамические силы;

§ переменное с течением времени гравитационное поле, обусловленное влиянием других небесных тел (кроме Земли) и в первую очередь Луны.

Эти обстоятельства необходимо учитывать при определении:

§ времени существования спутника на орбите;

§ географического положения спутника по отношению к поверхности Земли в каждый момент времени;

§ и т.д.

Задача точного расчета движения спутника является кропотливой и сложной. Если необходимо исследовать движение спутника на небольшом интервале времени (после запуска), то действительное движение можно заменить на более простое, сводя задачу к движению двух тел.

Задача будет более простой, если исходить из Кеплерового центрального поля тяготения и не учитывать сплюснутость Земли и ее суточные вращения. Траектория полета ИСЗ при этих допущениях представляет собой эллипс, в одном из фокусов которого находится центр Земного шара.

Частным случаем эллиптической траектории спутника является окружность с центром в центре Земного шара.

При выводе ИСЗ на ту или иную орбиту главный интерес представляют такие законы управления полетом ракеты-носителя, которые обеспечивают наименьшие энергетические затраты.

Пример: наименьший расход топлива необходимый для вывода ИСЗ на заданную орбиту.

Решение получается достаточно просто, если не принимать во внимание аэродинамические силы, действующие РН во время ее полета в плотных слоях атмосферы. Для спутника запущенного с поверхности Земли, такое решение будет иметь приближенный характер, а для спутника с Луны такое решение будет очень близко к действительному. Однако и для спутника с Земли такая постановка имеет смысл, т.к. позволяет сделать некоторые общие заключения.

Пренебрегая аэродинамическими силами будем считать, что на РН действует только сила тяги двигателей и сила тяжести Земли.

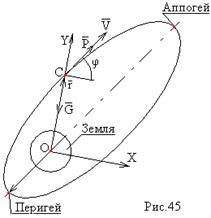В момент вывода ИСЗ на орбиту, кривизной Земли и ее суточным вращением пренебрегаем, а ускорение силы тяжести считаем постоянным для всех высот полета.

Задача заключается в отыскании такого закона и изменения силы тяги функции времени (по величине и направлению), чтобы на заданной конечной высоте полета (Н_к ) вертикальная составляющая скорости ИСЗ (V_ку), была равна нулю, а горизонтальная – (V_кх) имела максимальное значение.

Запишем уравнение движения ИСЗ в проекциях на оси координат OXY:

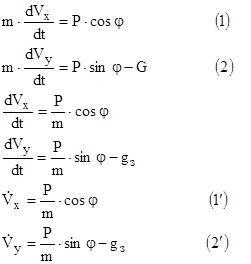
φ – угол между осью ОХ (земной системы координат) и осью двигателя (если двигатель соединен неподвижно с ракетой, то φ тождественен углу тангажа Θ).

Дата добавления: 2014-01-07