Основы работы и расчета на устойчивость центрально сжатых стержней

Исчерпание несущей способности длинных гибких стержней, работающих на осевое сжатие, происходит от потери устойчивости (рисунок а). Поведение стержня под нагрузкой характеризуется графиком (рисунок б):

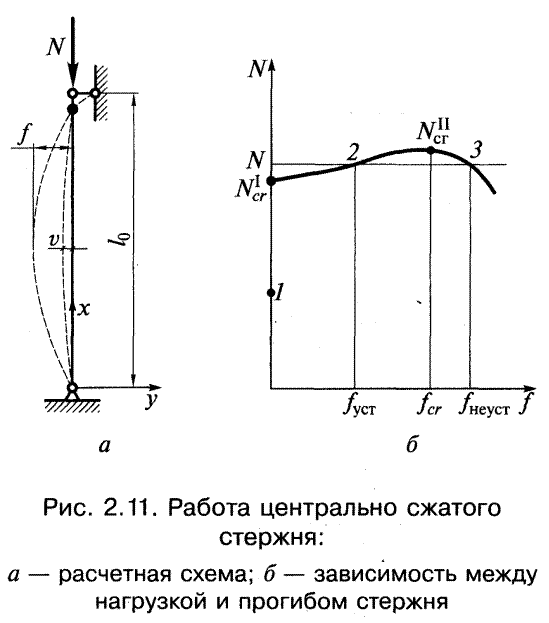
1. При увеличении нагрузки N от 0 до некоторой точки 1 сохраняется прямолинейная форма стержня, f=0.

2. При N=N_cr¹ стержень начинает резко выпучиваться.

3. Дальнейший (небольшой) рост нагрузки сопровождоется нарастанием поперечного прогиба стержня f.

4. При N=N_cr¹¹ стержень теряет несущую способность, то есть даже при устранении причины отклонения, стержень останется изогнутым.

Критическая сила для упругого, центрально сжатого, шарнирно – опертого по концам стержня определяется по формуле Л. Эйлера (1744 г.):

N

_,

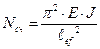где Е – модуль упругости материала стержня;

J – минимальный момент инерции сечения стержня;

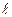_ef =μ·l₀– расчетная длина стержня.

Критические напряжения в стержне:

,

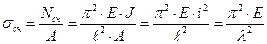где - площадь брутто поперечного сечения стержня;

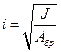– радиус инерции стержня;

–- гибкость стержня,

где 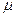– коэффициент приведения расчетной длины, учитывающий условия закрепления концов стержня;

₀ – геометрическая длина стержня.

Так как в приведенной формуле E-const, следовательно, она справедлива только в пределах прямой пропорциональности, то есть при σ_cr ≤ σ_p ≈ 20кН/см² для мягких сталей.

Минимальная гибкость стального стержня, выше которой формула Эйлера будет справедлива:

для мягких сталей ,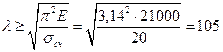

для сталей повышенной прочности .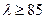

На практике гибкость центрально сжатых стержней составляет примерно половину указанных предельных, то есть стержни устраиваются настолько жесткими, что выпучивание наступает лишь после появления пластических деформаций. В этом случае

, где

Т – приведенный модуль продольного изгиба, зависящий от касательного модуля Е₁.

Таким образом, мы как бы заменяем изогнутый стержень из однородного материала с уменьшенным модулем упругости Т<Е, стержнем, в котором выделяем две зоны: растянутую, работающую по упругому закону, и сжатую, работающую по пластическому закону

Абсолютно прямолинейный стержень является идеализированной расчетной схемой. Все реальные стержни в натуре имеют неизбежные отклонения от прямолинейности (случайные эксцентриситеты ). Поэтому с самого начала загружения центрально сжатого стержня в нем возникает изгибающий момент , что ухудшает условия устойчивости стержня и снижает его критические напряжения. Поэтому в практических расчетах используют критические напряжения, вычисленные с учетом случайных эксцентриситетов. Величина случайных эксцентриситетов определяется статистическим изучением реальных стержней.

Устойчивость центрально сжатого стержня будет обеспечена, если напряжение в нем будут меньше критических:

, где

.- коэффициент устойчивости (коэффициент продольного изгиба), учитывает собственно явление продольного изгиба и влияние случайных факторов, вызывающих дополнительный поперечный изгиб.

или

.

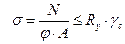Коэффициент устойчивости принимается по таблице 72 СНиП в зависимости от класса стали и гибкости элемента 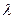, определяемой по формуле:

,

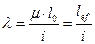Значения коэффициентов для сталей разных классов и некоторых алюминиевых сплавов приведены в нормах проектирования.

Дата добавления: 2014-01-07