Установленные для данной системы разрядная сетка и правило записи в ней двоичных чисел, называется форматом

Вита.

Алфавита.

011110100101₂ При переходе к 16-ричным числам двоичное число

разбивается на тетрады (четвёрки символов), каждая

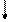
7А5₁₆ из которых записывается символами 16-ричного алфа-

К сожалению, не существует явных алгоритмов перевода чисел из 8- в 16- ричную систему счисления и обратно. Поэтому в этих случаях используется

710₈ В3С1₁₆ промежуточное двоичное

000111001000₂ 001011001111000001₂ представление: исходное

1С8₁₆ 131701₈ число переводится в двоичное, а затем по выше приведённому правилу - в искомое.

1.3. Формы представления двоичных чисел.

Чтобы обмен информацией между отдельными устройствами и системами стал возможен, необходимо выполнить как минимум два условия.

Во-первых, кодовые слова должны быть одинаковой длинны, иначе говоря - одинаковой разрядности. Действительно, во времени кодовые слова передаются непрерывно друг за другом и при различной длине сложно установить границу между ними. При одинаковой же длине для этого достаточно всего лишь каждый раз отсчитывать известное число разрядов.

Во-вторых, должно быть установлено определённое правило записи чисел в разрядной сетке. Это даёт возможность определить, например, положение старшего и младшего разрядов в изображении числа.

Для хранения чисел используются различные форматы: слово - с числом разрядов 32, полуслово - с числом разрядов 16, полуторное слово - с числом разрядов 48 и т.д.

Один разряд формата, как правило, старший, используется в качестве знакового, а остальные - для представления абсолютного значения числа. При этом знак "+" кодируется нулём, а знак "-" - единицей.

В формате числа могут быть представлены в одной из двух форм: с фиксированной или плавающей точкой. Рассмотрим эти формы, начиная с первой.

1). Представление чисел с фиксированной точкой (естественная форма представления чисел).

В этом случае точка, отделяющая целую часть числа от дробной может занимать одно из двух положений.

· Если точка расположена перед старшим разрядом, то абсолютное значение чисел меньше 1 и разрядная сетка предназначена для представления только их дробной части. При этом заполнение разрядной сетки начинается со старшего разряда. Формат представления таких чисел имеет вид:

Очевидно, что при n-разрядном формате можно

2⁰ 2^-1 2^-2 2^-n представить абсолютные значения дробных деся-

Х Х_n-1 X_n-2... X₀ тичных чисел в диапазоне от 0 до (1 - 2^-n)), где

Знак Абс. значение n - разрядная сетка без учёта знакового разряда.

· Если же точка фиксируется после младшего разряда, то абсолютное значение чисел больше или равно 1 и разрядная сетка предназначена для представления только их целой части. При этом заполнение разрядной сетки начинается с младшего разряда. Формат представления таких чисел имеет вид:

2ⁿ 2^n-1 2^n-2 2⁰ Очевидно, что при n-разрядном формате можно

X X_n-1 X_n-2... X₀ представить абсолютные значения целых десятич-

Знак Абс. значение ных чисел в диапазоне от 0 до (2ⁿ - 1).

При использовании формы с фиксированной точкой, как исходные данные, так и результаты их обработки должны быть всегда либо меньше 1, либо, наоборот, не меньше 1. Тогда для исключения ошибки необходимо предвидеть результаты обработки данных и соответствующим образом масштабировать их, т.е. умножать или делить на определённые коэффициенты. Однако прогнозировать результаты зачастую невозможно, поэтому необходимость в масштабировании является основным недостатком формы с фиксированной точкой.

2). Представление чисел с плавающей точкой.

В этом случае числа представляются в показательной форме: N = M*E^P, где М - мантисса числа, Р - порядок, а Е - основание системы счисления. М, Р и Е являются числами и записываются они символами данной системы счисления.

Например, десятичное число 6.73 в показательной форме будет иметь вид 673*10^-2 или 0.673*10¹. Аналогично запишется и двоичное число 11.01: 0.1101*10¹⁰ или 1101*10^-10

Отсюда видно, что абсолютное значение порядка равно числу разрядов, на которое смещена точка в изображении числа. Знак же порядка определяет направление смещения точки. Таким образом, с изменением значения порядка точка меняет своё положение, как бы "плавает" в изображении числа. Этим и определяется название формы.

В формате кодового слова двоичное число с плавающей точкой размещается, например, следующим образом:
Знак мантиссы При этом порядок всегда
P P_k-1 P_k-2... P₀ M M_n-1 M_n-2...M₀ число целое и записыва-

Знак порядка Абс. знач. пор. Абс. знач. ман. ется в формате по пра -
вилу записи целых чисел, а мантисса - по правилу дробных чисел.

Определим теперь диапазон десятичных чисел, которые могут быть обработаны системой при использовании формы с плавающей точкой.

Пусть К - число двоичных разрядов, отведённых для представления абсолютного значения порядка. Тогда минимальное двоичное число содержит (2^К - 1) нулей перед первой значащей единицей
N_min2 = 0.00...01 и в форме с плавающей точкой имеет вид:

2^k-1 N_min2 = 0.100...0*10^-11...1

где порядок состоит из К единиц. 2^k-1
Запишем это число в десятичной системе счисления: мантисса М равна 1/2 (действительно, 1000 соответствует 8-ми, его половина 0100 - четырём и т.д.), основание Е = 2, а порядок Р = -(2^К - 1). В результате получаем:
N_min10 = (1/2)2= .
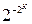Максимальное двоичное число содержит (2^К - 1) единиц N_max2 = 11...1 и в форме с плавающей точкой имеет вид: N_max2 = 0.11...1*10^11...1. Запишем это число в десятичной системе счисления: мантиссу можно принять равной 1, основание Е = 2, а порядок Р = 2^К - 1. В результате получаем: N_max10 = .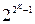

Таким образом, достоинством формы с плавающей точкой является значительное расширение диапазона обрабатываемых чисел.

Недостаток её в сложности реализации арифметических и других операций, что снижает быстродействие и усложняет структуру цифровой системы.

Поэтому форма с плавающей точкой применяется в универсальных ЭВМ, а с фиксированной точкой - в специализированных.

Дата добавления: 2014-01-07