
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Проектирование площадей графическим способом
|
|
|
|
Понятие о проектировании объектов в земельном кадастре.
Проектирование объектов в земельном кадастре сводится к проектированию площадей земельных участков и к проектированию вертикальной планировки на ней.
Проектирование земельных участков может вестись графическим способом, аналитическим, графоаналитическим и механическим. Проектирование вертикальной планировки осуществляется лишь аналитически с последующим графическим изображением проектных поверхностей.
Суть этого способа заключается в следующем.
Вначале на плане задаются определенной площадью, ограниченной конкретными точками. Эта площадь вычисляется графическим способом или аналитическим по координатам граничных точек. Находится разность между этой площадью и проектной. Эта разность может быть как положительной, так и отрицательной. Недостающую или избыточную площадь определяют графически на плане способами треугольника и трапеции.
Рассмотрим вначале способ треугольника. Пусть имеется некоторый земельный участок (рис. 14), в котором граничными являются точки ABCDE.
|

Рис. 14
Пусть необходимо запроектировать некоторую площадь Р таким образом, чтобы граничная линия проходила через точку Е.
Для решения этой задачи определяется площадь многоугольника BCDE. Находится разность между этой площадью и проектной, обозначим ее через Р 1. Если эта разность отрицательна, то к существующей площади в виде полигона BCDE необходимо добавить площадь Р 1 в виде треугольника BEF. Для построения точки F за основание треугольника а берется сторона ВЕ. Далее вычисляется высота треугольника h по формуле:
 (139)
(139)
где а берется с чертежа или вычисляется по координатам точек В и Е. Полученную высоту откладывают по перпендикуляру к ВЕ таким образом, чтобы она соединилась с прямой ВА. На соединение с этой прямой и фиксируется точка F.
В этом случае если площадь многоугольника BCDE больше проектной, то ее необходимо уменьшить на величину Р 1. Для этого по формуле () вычисляют высоту h. Ее откладывают по перпендикуляру к BF так, чтобы она соединялась с линией ВС. Точка соединения G и будет требуемой точкой перпендикуляра площади Р 1.
Проектирование трапециями выполняется в том случае, когда проектная линия должна проходить параллельно заданной. Весь процесс осуществляется последовательными приближенными.

|
Рис. 15
Вначале определяется исходная площадь полигона ABCD и сравнивается с проектной. Находится разность Р 1. Пусть эта разность положительная. Проектирование ведется параллельно одной из линий DA, BC или другой. Пусть необходимо запроектировать дополнительную площадь Р 1 параллельно стороне DA. Для этого в первом приближении определяется высота трапеции по формуле:
 (140)
(140)
Потом от стороны DA откладывается значение полученной высоты и проводится линия MN параллельно DA.
Измеряется длина линии MN и высота трапеции определяется второй раз:
 (141)
(141)
Если расхождение между полученными высотами в двух последующих приближениях не превышает 0,2 мм, то проектирование можно считать законченным. Проектным будет полигон MBCN.
Если это расхождение больше, то от стороны DA откладывают уже высоту  и проводят линию MN. Эта линия снова измеряется и находится последующее значение высоты трапеции по формуле (). После чего делается его сравнение с предыдущим значением и повторяются приближения.
и проводят линию MN. Эта линия снова измеряется и находится последующее значение высоты трапеции по формуле (). После чего делается его сравнение с предыдущим значением и повторяются приближения.
§1. ПРОЕКТИРОВАНИЕ НЕСКОЛЬКИХ УЧАСТКОВ ГРАФИЧЕСКИМ СПОСОБОМ.
Пусть имеется некоторый четырехугольник (рис. 16), внутри которого необходимо запроектировать несколько земельных участков с определенными площадями.

|
При этом полагается, что стороны AD и ВС исходного полигона параллельны между собой. Пусть проектирование ведется параллельно этим сторонам способом трапеций и получены их высоты 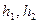 … Необходимо определить отрезки
… Необходимо определить отрезки  на боковых сторонах AB и CD, которые будут использоваться для закрепления запроектированных площадей. Из подобия треугольников можно записать:
на боковых сторонах AB и CD, которые будут использоваться для закрепления запроектированных площадей. Из подобия треугольников можно записать:
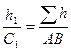
Тогда
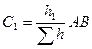
В общем случае

Аналогично

§2. АНАЛИТИЧЕСКИЙ СПОСОБ ПРОЕКТИРОВАНИЯ ПЛОЩАДЕЙ.
В основу проектирования данным способом также положены треугольник и трапеция.
Рассмотрим в начале применение треугольника.
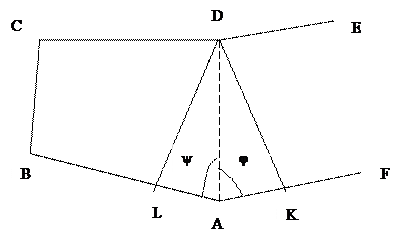 Рис. 17
Рис. 17
Пусть необходимо запроектировать площадь, большую площади многоугольника ABCD на Р1. Будем считать координаты граничных точек А, В, С … известными. Проектная линия будет проходить через точку D. Необходимо на местности определить положение точки К, соответствующей проектной площади.
Из решения обратной геодезической задачи находится длина и дирекционный угол линии DA. По дирекционным углам линии DA и АУ находится угол:
 (142)
(142)
Площадь Р 1 треугольника ADK равна
 (143)
(143)
Исходя из этой формулы (144)
(144)
На местности откладывают отрезок АК и фиксируют точку К 1 соответствующую проектной площади.
Аналогично выполняются действия по проектированию площади, меньше заданной на Р 1. При этом положение точки L определяется с помощью угла ψ по отрезку AL (рис. 17).
Способ трапеции применяется для проектирования линий, параллельных заданной.
Пусть необходимо запроектировать линию CD, ограничивающую проектную площадь Р 1, параллельно линии АВ (рис. 18).

Рис. 18
Принимается, что углы α и β известны. Известна площадь фигуры ABCD. Необходимо определить длину стороны b, а также отрезки ВС и AD, необходимые для закрепления точек С и D вдоль соответствующих направлений.
Для решения поставленной задачи сторона CD проектируется на АВ. В результате такого проектирования получают отрезки x и y на линии АВ относительно точек А и В.
x = h ctg α
y = h ctg β (145)
Если принять
AB = a
CD = b,
то можно записать, что
a – b = x + y = h (ctg α + ctg β) (146)
Поскольку площадь трапеции равна
 (147)
(147)
то с учетом () можно записать
 (148)
(148)
или
 (149)
(149)
Из () можно найти b
 (150)
(150)
Подстановка () в () приводит к значению высоты h.
 (151)
(151)
по которой вычисляются элементы,
 (152)
(152)
необходимые для осуществления выноса в натуру точек C и D. По ним могут быть вычислены и координаты этих точек. Контролем правильности проектирования является вычисление площади всего участка по координатам, она должна равняться проектной.
Способы треугольника и трапеции могут применяться в комбинации, например (рис. 19).
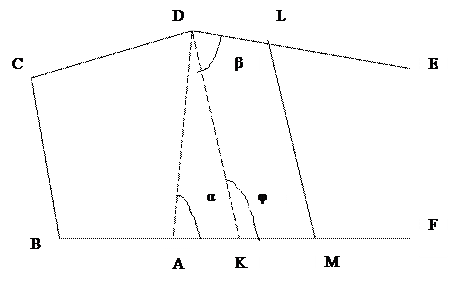 Рис. 19
Рис. 19
Вначале может быть запроектирована площадь в виде треугольника DAK. Далее недостающая площадь может быть добавлена в виде трапеции DKLM. При этом значение стороны DK необходимое для проектирования трапеции вычисляется по координатам точек D и К из решения обратной геодезической задачи. А углы φ и ∂ находятся по дирекционным углам сторон DK, DE и AF.
То есть

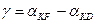
Угол φ находится так

 При проектировании массива участков (рис. 19) поступают следующим образом
При проектировании массива участков (рис. 19) поступают следующим образом
Рис. 19
Весь массив разбивается на трапеции 1, 2, 3 … Их основания параллельны исходной стороне АВ. Для проектирования линии KL, MN новых земельных участков поступают следующим образом.
Для проектирования участка ABKL способом трапеций проектируется линия KL относительно стороны СС'. Для проектирования участка KLMN вначале вычисляется площадь KLDD', а способом трапеций проектируется недостающая площадь DD'MN и соответствующая проектная линия MN.
§3. ГРАФОАНАЛИТИЧЕСКОЕ ПРОЕКТИРОВАНИЕ.
Этот способ проектирования является комбинацией графического и аналитического проектирования. При этом вначале выполняется графическое, а на его основе осуществляется аналитическое.
Пусть в четырехугольнике ABCD (рис. 20) осуществлено графическое проектирование и получены высоты 
 Рис. 20
Рис. 20
Это есть первое приближение графоаналитического проектирования.
Во втором приближении по формуле:
b = a * h (ctg α + ctg β)
находятся вторые основания трапеций.
По ним вычисляются площади запроектированных трапеций по формуле:
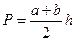
Если эти площади отличаются от проектных на недопустимую величину, то вычисляются уточненные высоты. Их вывод заключается в следующем.
Поскольку
 (153)
(153)
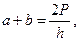 (154)
(154)
то
 (155)
(155)
на основании () можно записать формулу для вычисления высот способом приближений
 (156)
(156)
Приближения по формуле () повторяются до тех пор, пока последующее значение высоты h i+1 не совпадает с предыдущим hi с точностью вычислений. Боковые стороны вычисляются по формулам:

§4. МЕХАНИЧЕСКИЙ СПОСОБ ПРОЕКТИРОВАНИЯ ПЛОЩАДЕЙ.
Настоящий способ применяется в случае, когда границы участков являются не ломаными линиями, а кривыми.
В этом случае запроектированную на глаз площадь определяют планиметром, а недостающую или избыточную площадь по сравнению с проектной проектируют графическим способом.

Рис. 21
Так на рисунке 21 плоащь, ограниченная линией АВ, определяется планиметром. Недостающая площадь Р 1 проектируется графически способом трапеций.
После этого определяется площадь ограниченная уже линией MN и процесс приближенный повторяется, пока не будет получена проектная площадь с определенной точностью.
§5. ТОЧНОСТЬ ПРОЕКТИРОВАНИЯ ПЛОЩАДЕЙ ГРАФИЧЕСКИМ СПОСОБОМ.
При этом возможны два случая.
I случай. Проектирование выполняется на базе теодолитного хода, проложенного по границе существующего участка.
Тогда на точность проектирования будут влиять следующие факторы.
- точность угловых и линейных измерений в ходе;
- точность нанесения на плане его точек по координатам;
- точность проектирования с использованием графического способа определения недостающей или избыточной площади.
Средняя квадратическая ошибка площади, вызванной точностью угловых и линейных измерений в ходе, может быть оценена по формуле:
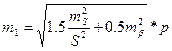 (157)
(157)
Средняя квадратическая ошибка, вызванная ошибкой нанесенных точек по координатам, может быть оценена по формуле:
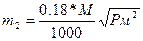 (158)
(158)
где 0.18 мм – средняя квадратическая ошибка нанесения точки на план.
Средняя квадратическая ошибка собственно графического проектирования будет:
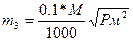 (159)
(159)
Общая средняя квадратическая ошибка будет:
 (160)
(160)
II случай. Проектирование ведется на основе контурных точек.
Здесь имеют место следующие факторы: точность положения контурных точек и точность собственного графического проектирования.
Первый фактор здесь определяется формулой (158), в которой вместо 0.18 мм необходимо подставить точность положения контура 0.5 мм. Второй фактор соответствует значению m3. Общая средняя квадратическая ошибка будет:
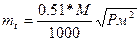 (161)
(161)
Аналитический способ.
В этом способе точность проектирования целесообразно характеризовать формулой (97).

Механический способ.
Средняя квадратическая ошибка проектирования площади может быть оценена по формуле (136) при однократном обводе площади планиметром.

ГЛАВА 4. ВЕРТИКАЛЬНАЯ ПЛАНИРОВКА ТЕРРИТОРИИ.
§1. ОБЩИЕ ЗАМЕЧАНИЯ ПО ВЕРТИКАЛЬНОЙ ПЛАНИРОВКЕ.
Вертикальная планировка осуществляется проектированием горизонтальной плоскости, наклонной плоскости и поверхности, описываемой уравнением вида:
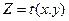 (162)
(162)
где Z – проектная отметка, x. y – координаты точки местности в принятой системе координат.
При этом частным случаем уравнения (162) может быть, например, полином второй степени
 (163)
(163)
В этом случае по заданным значениям A, B, C, D, E, F вычисляются проектные отметки Z точек с координатами x и y.
§2. ПРОЕКТИРОВАНИЕ ГОРИЗОНТАЛЬНОЙ ПЛОСКОСТИ.
На участке местности, где необходима вертикальная планировка, разбивается сетка квадратов со стороной квадрата определенной длины (рис. 22).
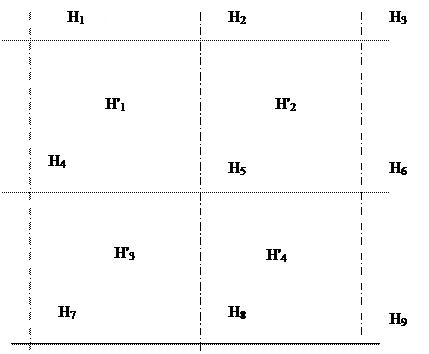
Рис. 22
Определяются отметки вершин сетки квадратов H1, H2, … H9. На этой основе выполняется расчет проектной отметки горизонтальной плоскости. Суть его заключается в следующем.
Вначале определяются отметки центров квадратов

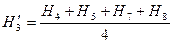 (164)
(164)


По этим данным находится проектная отметка как среднее арифметическое
 , (165)
, (165)
где n – число квадратов.
Если выражения () подставить в (), то получим
 (166)
(166)
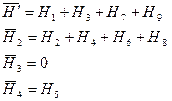
соответственно суммы отметок вершин, принадлежащих одному, двум, трем и четырем квадратам.
Для некоторого упрощения расчетов в сетке квадратов выбирается точка с наименьшей отметкой Н относительно ее выписываются превышения двух точек по формуле: hi = Hi – H, (167)
а проектная отметка вычисляется так
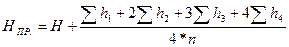 (168)
(168)
По проектной отметке и фактическим вычисляются рабочие отметки ri в каждой вершине сетки квадратов.
ri = Hпр. – Hi, (169)
По рабочим отметкам вычисляются положения точек нулевых работ в соответствии с известной формулой

Рис. 23
По точкам нулевых работ проводится линия нулевых работ, с помощью которой отделяется зона насыпи от зоны выемки грунта на участке. Зону выемки обычно штрихуют. Полученный чертеж называют картограммой земляных работ.
По построенной картограмме вычисляют объемы земляных работ.
§3. ПРОЕКТИРОВАНИЕ НАКЛОННОЙ ПЛОСКОСТИ.
Положение наклонной плоскости определяется ее начальной точкой и углами: вдоль оси абсцисс ix и вдоль оси ординат iy. Тогда отметка любой точки сетки квадратов найдется из формулы
 (170)
(170)
где dx, dy – соответственно расстояния от начальной точки с проектной отметкой Н0 до текущей (рис. 24).
 |
Рис. 24
Значения H0, ix, iy задаются по проекту.
 Проектирование наклонной местности выполняется аналогично горизонтальной.
Проектирование наклонной местности выполняется аналогично горизонтальной.
Вначале по формуле () вычисляются проектные отметки точек сетки квадратов.
По проектным отметкам и фактическим находятся рабочие отметки. По рабочим отметкам определяется положение точек нулевых работ. Строиться картограмма земляных работ и вычисляются объемы земляных работ. В соответствии с проектом определяются в отношении баланса земляных работ. Если необходимо, то изменяя уклоны ix, iy, а также Н0 добиваются баланса земляных работ, т.е. равенства объемов насыпи и выемки грунта. В других случаях решения могут быть иными.
§4. ВЫЧИСЛЕНИЕ ОБЪЕМОВ ЗЕМЛЯНЫХ РАБОТ.
Существуют различные способы вычисления объемов земляных работ. Наиболее распространенные из них следующие: квадратов, вертикальных и горизонтальных профилей.
В способе квадратов объема тела определяется следующим образом
 (171)
(171)
где ri – рабочие отметки вершин квадрата (рис. 25), а a – длина стороны квадрата.

Рис. 25
Формула () справедлива для того случая, когда основанием тела является квадрат.
Если же его основанием является треугольник (рис. 26), то объем вычисляется по формуле:
 (172)
(172)
где S – площадь основания в виде треугольника.

Рис. 26
Если основанием такой пирамиды является пятиугольник (рис. 27)
 Рис. 27
Рис. 27
То объем вычисляется по формуле
V5 = V4 – V3
Способ вертикальных профилей применяется для вычисления объемов вытянутых точек (рис. 28) каналов, дорог и др.
 Рис. 28
Рис. 28
При этом объем вычисляется по формуле
 (173)
(173)
Способ горизонтальных профилей применяется при проектировании вертикальной планировки построениями проектных горизонталей (рис. 29).
 (174)
(174)
а объем тела с вершиной в точке А и основанием S2 по формуле пирамиды
 (175)
(175)
В (), (), n – высота сечения рельефа, h – превышения точки В над точкой А.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 459; Нарушение авторских прав?; Мы поможем в написании вашей работы!