Оценка устойчивости системы

При оценке адекватности модели реально может быть использовано лишь ограниченное подмножество всех возможных значений входных параметров (рабочие нагрузки и среды). В связи с этим, для обоснования достоверности полученных результатов моделирования большое значение приобретает проверка устойчивости модели.

Устойчивость модели – это ее способность сохранять адекватность при исследовании эффективности системы на всем возможном диапазоне рабочей нагрузки, а также при внесении изменений в конфигурацию системы.

Универсальной процедуры проверки устойчивости модели не существует. Разработчик вынужден прибегать к методам «для данного случая», частичным тестам и здравому смыслу.

Часто бывает полезно апосториорная (послеопытная) проверка, которая состоит в проверке результатов моделирования и результатов измерений. Если результаты моделирования приемлемы, то уверенность в устойчивости модели возрастает. В общем случае можно утверждать, что чем ближе структура модели к структуре системы, тем устойчивее модель.

Устойчивость результатов моделирования может быть также оценена методами математической статистики, основная идея которых заключается в том, чтобы проверить гипотезу относительно свойств генеральной совокупности, оценивая лишь конкретную выборку из генеральной совокупности.

В генеральной совокупности обычно интересует некоторый признак, который обусловлен случайностью и может иметь качественный или количественный характер.

В данном случае именно устойчивость результатов моделирования можно рассматривать как признак, подлежащий оценке.

Для проверки гипотезы об устойчивости результатов может быть использован критерий Уилколсона.

Этот критерий служит для проверки гипотезы относительно того, что две выборки относятся к одной и той же генеральной совокупности (например, в двух партиях некоторой продукции измеряется определенный признак), и требуется проверить гипотезу о том, что в обеих партиях этот признак имеет одинаковое распределение, т.е. убедиться, что технологический процесс от партии к партии изменяется несущественно.

При статистической оценки устойчивости модели гипотеза формулируется следующим образом. При изменении входной (рабочей) нагрузки или структуры имитационной модели закон распределения результатов моделирования остается неизменным.

Проверку указанной гипотезы Н проводят при следующих исходных данных: есть две выборки X=(x₁, x₂, …, x_n) и Y=(y₁, y₂, …, y_n). Полученные данные для различных значений рабочей нагрузки и относительного распределения X, Y, никаких предположений не делается. Значение обеих выборок упорядочиваются вместе по возрастанию. Затем анализируется взаимное расположение (x_i, y_j). В случае, если y_j<x_i говорят, что пара значений (x_i, y_j) образует инверсию.

Например, пусть n=m=3, а после упорядочивания по возрастанию образовалась последовательность: y₁, x₁, y_3, x₂, y₂, x₃.

Тогда имеем инверсии: (x₁, y₁) (x₂, y₁) (x₂, y₃) (x₃, y₁) (x₃, y₂) (x₃, y₃).

Подсчитывают полное число инверсий U. Если гипотеза верна, то U не должно сильно отличаться от своего мат. ожидания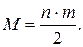

От гипотезы отказываются, если | U-M|>U_кр, где U_кр – критическое значение критерия (берется по таблице).

Дата добавления: 2014-01-07