Теоремы теории игр

Теорема 1. (основная теорема теории игр).

Всякая конечная игра имеет цену и у каждого игрока существует по меньшей мере одна оптимальная стратегия.

Терема 2. Нижняя цена игры всегда не превосходит верхней цены игры, .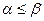

Рассмотрим два случая.

1. Пусть .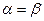

Игра, для которой, 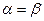, называется игрой с седловой точкой. Если 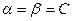, то С является ценой игры, а стратегии игроков, обеспечивающие им выигрыш или проигрыш, равный С, являются опти­мальными. Если игра с седловой точкой имеет С=0, то она является справедливой, если С0, - несправедливой.

2. Пусть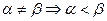. В этом случае трудно определить цену игры и оптимальные стратегии игроков. Вернемся к рассмотренному приме­ру. = 3, а = 5. Значит, первый игрок может гарантировать себе выигрыш, равный 3, а второй - ограничить свой проигрыш 5. Область между и является как бы ничейной, и каждый игрок может попы­таться улучшить свой результат за счет этой области. Каковы в этом случае оптимальные стратегии игроков? Если каждый игрок будет при­менять стратегию, соответствующую его максимальному гарантированному выигрышу или проигрышу, противник может догадаться о его намерениях и улучшить свой результат. Например, первый игрок использует х₃, а второй - y₂. Второй игрок заметил, что первый все время применяет x₃, и решил применить y₁, сведя свой проигрыш к меньшему числу. Таким образом, чтобы иметь успех, каждый игрок должен хранить свой выбор в секрете. Это трудно сделать, если игра повторяется многократно.

Секретность можно сохранить, если каждый раз выбирать страте­гию случайным образом (бросая монету, кость и т.п.). При этом вы­игрыш и проигрыш будут случайными величинами. Результат можно оце­нить средней величиной проигрыша или выигрыша. Так, в нашем случае, если второй игрок использует свои стратегии y₁, y₂, y₃ случайным образом, например, с вероятностями 1/3; 1/3; 1/3, соответственно, то среднее значение его проигрыша может быть:

- если первый использует х₁:

С_ср = 1/3 а₁₁ + 1/3 а₁₂ + 1/3 а₁₃ = 7/3 + 2/3 + 5/3 = 14/3;

- если первый использует х₂:

С_ср = 1/3 а₂₁ + 1/3 а₂₂ + 1/3 а₂₃ = 2/3 + 2/3 + 3/3 = 7/3;

- если первый использует х₃:

С_ср = 1/3 а₃₁ + 1/3 а₃₂ + 1/3 а₃₃ = 3/3 + 5/3 + 4/3 = 4. Таким образом, второй игрок может ограничить свой проигрыш уже не 5, а 14/3, независимо от стратегии первого игрока. Следователь­но, в ряде случаев оказывается целесообразным не намечать заранее стратегии, а выбирать ту или иную случайным образом. Стратегия, основанная на случайном выборе, называется смешанной стратегией.

Вектор, каждая компонента которого показывает относительную частоту (вероятность) использования игроком соответствующих чистых стратегий, называется смешанной стратегией.

Пусть u=(u₁,...,u_m) и z=(z₁,...,z_n), соответственно, вероятности отдельных исходов механизма случайного выбора 1-го и 2-го игроков.

Из теории вероятностей должно быть известно, что

1) u_i 0, i=; z_j. 0, j=; (т.к. 0р 1);

2) и (т.к. р(U) = 1, U- достоверное событие). Если u^* - оптимальная стратегия 1-го игрока, z^* - оптималь­ная стратегия 2-го игрока, то число 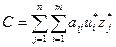является ценой игры.

Определение оптимальных стратегий и цены игры составляет процесс решения игры.

Теорема 3 (о цене игры).

Всякая матричная игра с нулевой суммой имеет решение в смешанных стратегиях. Для того, чтобы число С было ценой игры, а u^* и z^* - оптимальными стратегиями игроков, необ­ходимо и достаточно выполнения неравенств:

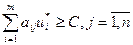и .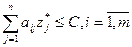

Теорема дает ответ на вопрос о существовании решения игры и определяет путь решения.

В частном случае, когда по крайней мере у одного из игроков имеется только 2 стратегии, справедлива теорема.

Теорема 4. Если один из игроков применяет оптимальную смешанную стратегию, то его выигрыш или проигрыш равен цене игры вне зависимости от того, с какими частотами (вероятнос­тями) будет применять другой игрок свои стратегии, вошед­шие в оптимальную.

3. Способы решения задач теории игр.

4. Методы принятия решений: в условиях определенности; в условиях риска; в условиях неопределенности.

До сих пор рассматривались игры, в которых участвовали два, как бы равноправные, противника, преследовавшие противоположные цели. Каждый стремился так выбрать свою стратегию, чтобы получить для себя наибольшую выгоду и свести до минимума выгоду противника.

Однако, во многих практических ситуациях приходится сталки­ваться со случаями, когда один из противников оказывается нейт­ральным, т.е. таким, который не стремится извлечь для себя макси­мальную выгоду, а, следовательно, не стремится обратить в свою пользу ошибки, совершаемые противником. К таким играм относят иг­ры, в которых в качестве одного из игроков выступает "природа".

Здесь в понятие "природа" входит вся совокупность внешних обстоя­тельств, в которых приходится принимать решение. Любая хозяйс­твенная деятельность человека может быть представлена как игра с "природой".

Человек в играх с "природой" старается действовать осмотри­тельно, используя, например, минимаксную стратегию, позволяющую получить наименьший проигрыш. "Природа" действует совершенно слу­чайно, возможные стратегии определяются как ее состояния (напри­мер, условия погоды, спрос на определенную продукцию, объем пере­возок, некоторое сочетание производственных факторов и т.п.).

Неизбежной платой за попытку получить решение в условиях не­полной информации о законе "природы", является возможность приня­тия ошибочных решений. Качество решений зависит от информирован­ности, его квалификации. При этом, на практике бывают ситуации, в которых отказаться от решения вообще невозможно. К тому же отказ от решения есть тоже решение, которое может иметь столь же неже­лательные последствия. Выход - выработка человеком такой страте­гии в отношении принятия решения, которая хотя и не исключает возможность принятия неправильных решений, но сводит их к миниму­му. Для того, чтобы решить свою задачу - принять наилучшее реше­ние в каждой конкретной ситуации, человек имеет возможность изу­чать "природу" - проводить эксперимент. Этому мешают два обстоя­тельства: время и затраты.

Игры, в которых один противник "природа", а другой - чело­век или, в которых один из игроков действует несознательно, а в соответствии с определенными законами, называются играми с "природой" или статистическими играми.

Теория таких игр - теория статистических решений. Человек, который участвует в игре против природы, называется статистиком (экономистом).

В теории принятия решений используют «разумные» процедуры выбора наилучшей из нескольких возможных альтернатив. Насколько правильным будет выбор, зависит от качества данных, используемых при описании ситуации, в которой принимается решение. С этой точки зрения процесс принятия решений может принадлежать к одному из трез возможных условий:

1. Принятие решений в условиях определенности, когда данные известны точно.

2. Принятие решений в условиях риска, когда данные можно описать с помощью вероятностных распределений.

3. Принятие решений в условиях неопределенности, когда данным нельзя приписать относительные веса, которые представляли бы степень их значительности в процессе принятия решений.

Рассмотрим все эти условия.

Дата добавления: 2014-01-07